3. Параллельное проецирование

Частный случай центрального проецирования с центром проекций, находящимся в бесконечности (в несобственной точке O). Осуществляется связкой лучей заданного направленияS(рис. 2).

Аппарат параллельного проецирования:

  плоскость проекций;

S— направление проецирования;

[O_A][O_B] S

A^= [OA]  — параллельная проекция точки А на плоскость ;

l^= (AA^BB^) —параллельная проекция прямой на плоскость .

Обратимости нет. Одна центральная проекция точки не позволяет судить о положении точки в пространстве. А = D

4. 

   Рис. 2

   Инвариантные свойства параллельного проецирования

Геометрические фигуры проецируются на плоскость проекций, в общем случае, с искажением. Характер искажений зависит от аппарата проецирования и положения проецируемой фигуры относительно плоскости проекций.

В частности, при параллельном проецировании нарушаются метрические характеристики геометрических фигур (искажаются линейные и угловые величины). Некоторые свойства фигуры сохраняются на ее проекции.

Сохраняющиеся в проекции свойства фигуры называются независимыми или ИНВАРИАНТНЫМИ. Эти инвариантные свойства часто называют сокращенно: инварианты.

Инварианты параллельного проецирования

1. Проекция точки есть точка (рис. 1; рис.2)

2. Проекция прямой есть прямая (рис. 1; рис.2)

^

3. Проекция точки, принадлежащей прямой, принадлежит проекции.

этой прямой (рис. 1; рис.2)

4. Проекция точки пересечения прямых определяется пересечением проекций этих прямых (рис. 3)

5. Проекции взаимно параллельных прямых взаимно параллельны (рис. 4)

6. Отношение длин отрезков взаимно параллельных прямых равно отношению длин их проекций (рис. 4)

СЛЕДСТВИЕ:если отрезок прямой делится точкой в каком-либо отношении, то проекция отрезка делится проекцией этой точки в том же отношении (рис. 5)

7. Плоская фигура, параллельная плоскости проекций, проецируется на эту плоскость в конгруэнтную фигуру (рис. 6)

Рис. 3 Рис. 4

Рис. 5 Рис. 6

5. Прямоугольное (ортогональное) проецирование

Частный случай параллельного проецирования, при котором напраление проецирования перпендикулярно плоскости проекций (рис. 7)

В дальнейшем безоговорочно используется ортогональное проецирование.

В ортогональном проецировании сохраняются все свойства параллельного проецирования. Кроме того, для ортогонального проецирования справедлива теорема о проецировании прямого угла (смотри тему №6) и применим способ определений расстояния между точками (т.е. длины отрезка, смотри тему №3), называемый способом прямоугольного треугольника.

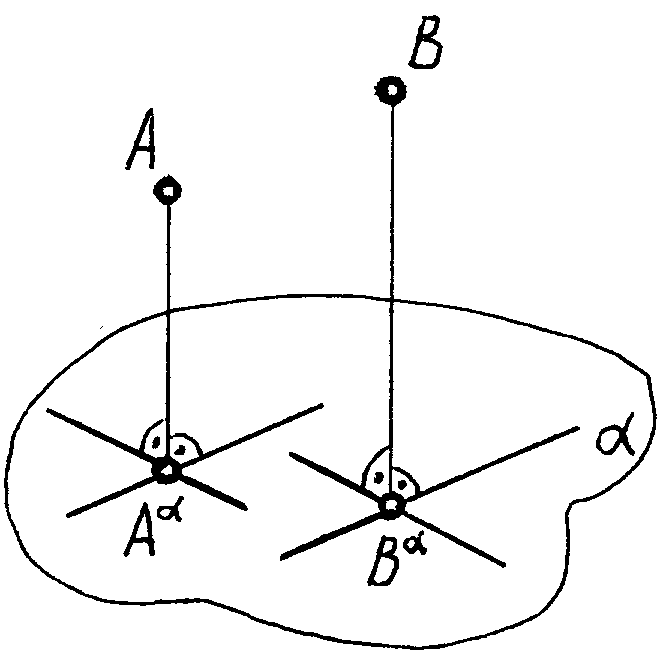
Рис. 7

БОЛЕЕ ПОДРОБНО...

Положение предмета в пространстве определяют четыре его точки, не лежащие в одной плоскости. Изображение пространственного предмета на чертеже сводится к построению проекций множества точек этого предмета на плоскости R(называемой плоскостью проекций) при помощи прямых линий (проецирующих лучей), проходящих через точки предмета и направленных к центру проецированияS.

Однако, чтобы построить проекцию предмета, не обязательно строить все его точки. Достаточно найти лишь проекции характерных точек (вершин, ребер и т.п.), которые затем соединить соответствующей линией.

Проецирующие лучи в совокупности образуют проецирующую поверхность. Так, при проецировании прямой АВ проецирующей поверхностью является плоскость АВba(рис. ).

Линия пересечения abпроецирующей плоскости с плоскостьюRпредставляет собой проекцию прямойAB, которая слагается из проекций отдельных ее точек.

Проекция подобна тени, отброшенной от предмета, освещенного лампой или солнцем.

При проецировании кривой линии в первом случае проецирующие лучи образуют коническую поверхность с вершиной в точке S, получаетсяконическое(перспективное) изображение кривой (рис. 2). Во втором случае конус проецирующих лучей превращается в цилиндр и коническое изображение переходит в цилиндрическое (параллельное) (рис. 2). Проекция кривой линии рассматривается при этом как линия пересечения проецирующей поверхности с плоскостьюR.

В перспективе предмет изображается таким, каким он представляется глазу наблюдателя. Хрусталик глаза является центром проецирования. Каждому из нас знакомо следующее явление: если смотреть вдоль полотна железной дороги, нам кажется, что рельсы как бы сближаются между собой и на горизонте сходятся в одну точку (центр), а опоры, расположенные вдоль путей, уменьшаются по мере удаления.

Параллельное проецирование — частный случай перспективы. Суть параллельного проецирования заключается в следующем: если условно удалить центр проецирования в бесконечность, то проецирующие лучи можно считать параллельными.

Так, чтобы построить параллельную проекцию треугольника ABC(рис. ), нужно задать:R— плоскость проекций (не параллельную и не совпадающую с направлением проецирующих лучей);S— направление проецирующих лучей (направление проецирования).

Далее, через характерные точки предмета проводят проецирующие лучи Аа,ВbиСспараллельно направлению проецирования, а затем находят точкиa,bи с их пересечения с плоскостьюR. Эти точки — искомые параллельные проекции точекА,ВиСзаданного треугольника.

Проекция abc— линия пересечения проецирующей призматической поверхности с плоскостьюR. Форма и размеры параллельной проекции какого-либо предмета при заданном направлении проецирования зависят только от выбора направления плоскости проекций и не зависят от ее удаления от предмета. Треугольник, расположенный в плоскостиR₁, параллельной плоскости проекций, проецируется равным заданному. В этом случаеab=AB,bc=BC,ac=AC.

В зависимости от угла наклона проецирующего луча к плоскости проекций параллельное проецирование делится на два вида: прямоугольное и косоугольное.

ПРЯМОУГОЛЬНЫМ (или ортогональным) проецирование называется в том случае, когда направление проецирования выбрано перпендикулярным плоскости проекций. В другом случае оно называетсяКОСОУГОЛЬНЫМ.

При прямоугольном проецировании (рис. 7) величина коэффициента искажения не может превышать единицы.

В косоугольных проекциях (рис. 5) коэффициент искажения (К=ab/AB) данного отрезкаАВможет принимать любые числовые значения в зависимости от наклона отрезка и проецирующих лучей к плоскости проекций. В частности, если направление отрезка совпадает с направлением проецирования, то проекцией этого отрезка будет точка, а коэффициент искажения равен нулю.

В параллельном проецировании сохраняются основные свойства перспективы, а именно:

1) проекция точки есть точка;

2) проекция прямой в общем случае будет прямая;

3) каждой точке, принадлежащей какой-либо линии, соответствует проекция этой точки на проекции данной линии.

Кроме того, параллельное проецирование имеет еще ряд (только ему присущих) свойств:

4) если точка лежит на отрезке прямой, то проекция этой точки делит проекцию отрезка в том же отношении, в каком

точка делит отрезок, т.е. AC/CB=ас/cb(рис. 5);

5) проекцией пересекающихся отрезков будут также пересекающиеся отрезки, а точка их пересечения будет проекцией точки пересечения данных отрезков (рис. 3);

6) проекции параллельных отрезков параллельны, одного направления, а их отношение равно отношению длин отрезков, т.е. abcdиAB/CD=ab/cd(рис. 4);

7. при прямоугольном проецировании прямой угол проецируется прямым углом только в том случае, если одна из его сторон параллельна плоскости проекций, а вторая не является проецирующим лучом (теорема о проецировании прямого угла).