Andrieiev_Teoretychna_mekhanika_2014

Таблиця 2.2 – Варіанти розрахункових схем для визначення реакцій опор при дії плоскої системи сил

41

Продовження табл. 2.2

42

Продовження табл. 2.2

43

Продовження табл. 2.2

44

Таблиця 2.3 – Вихідні дані для визначення реакцій опор при дії плоскої системи сил

45

2.3. Визначення реакцій складеної конструкції при дії плоскої системи сил

Необхідно визначити сили реакцій для розрахункової схеми, наведеної на рис. 2.9 а, при таких вихідних даних:

F 10 кН; q 10 кН/м; M 10 кН м; a 4 м;b 3 м;c 1,5 м; 60 .

Розв’язок проведемо за наступною схемою:

1.Об’єктом рівноваги є система двох стержнів, з’єднаних у точці

Сшарніром. Система навантажена зосередженою силоюF , парою сил із моментом M та розподіленою силою інтенсивністю q .

2.Обираємо систему координат xAy .

3.У точці А система закріплена за допомогою жорсткого закріплення, у точці В – за допомогою шарнірно-рухомої опори.

4.Жорстке закріплення замінимо двома складовими: X A ,YA , ша-

рнірно-рухому – силою RB , спрямованою по горизонталі (рис. 2.9 б).

5.Розподілену силу замінимо зосередженою силою Q (див. рис.

2.9б), модуль якої Q q c 10 1,5 15кН, точка прикладання її розташована у середині відрізку дії вихідної розподіленої сили.

6.Сила F у обраній системі координат є нахиленою до осей, тому замінюємо її відповідними складовими: Fx и Fy (див. рис. 2.9 б):

Fx F cos , Fy F sin , 30 ;

7. Розділяємо конструкцію на два окремі ламані стержні, замінюючи відкинуті частини силами XC ,YC , спрямованими так, як показано на рис. 2.9 в.

8. Складаємо рівняння рівноваги окремо для лівої частини (див.

рис. 2.9 в):

X A XC 0;

YA Q YC 0;

M A M Q 0,5c YC b XC a 0,

46

окремо для правої частини (див. рис. 2.9 в):

XC RB Fx 0;

YC Fy 0;

Fy d Fx e RB f 0,

в

Рисунок 2.9 – Розрахункова схема для визначення реакцій опор складеної конструкції: а – вихідна схема; б – звільнена система з перетвореними

силами; в – розділена по шарніру система

47

Розв’язуючи ці дві системи рівнянь разом, одержуємо такі результати:

X A 2,89кН;YA 20кН; M A 2,2кН м;

RB 11,55кН; XC 2,89кН;YC 5кН.

По одержаних результатах можна визначити величини повної реактивної сили у закріпленні А та сили, яка виникає у з’єднувальному шарнірі С:

Далі розглянемо розв’язок цієї задачі засобами ПК КіДиМ.

Текст файлу

РАБОТА:=№1.2; ВЫПОЛНИЛ:= студент Иванов А.А., Гр. І-10а;

# Запис рівнянь рівноваги #

P.x1=Xa+Xc;

P.y1=Ya-Q+Yc;

P.fi1=Ma-M+Q*c/2+Yc*b-Xc*a; P.x2=-Xc-Rb+F*cos(alfa-gamma); P.y2=-Yc-F*sin(alfa-gamma);

P.fi2=-F*sin(alfa-gamma)*b*cos(PI/6)- F*cos(alfa-gamma)*b*sin(PI/6)+Rb*(b+c)*sin(PI/6);

# Вихідні дані та необхідні розрахунки # gamma=PI/6; Q=q*c;

F=10; q=10; M=10; a=4; b=3; c=1.5; Ra=sqrt(Xa^2+Ya^2); Rc=sqrt(Xc^2+Yc^2);

Re1=abs((Rc-Ra)*100/Ra);

Re2=abs((Rc-Rb)*100/Rc);

#Інструкції для розв’язку та представлення результатів#

НЕИЗВЕСТНЫЕ:= Xa,Ya,Rb,Ma,Xc,Yc; alfa=alfaG*PI/180;

ВАРЬИРОВАТЬ:= alfaG(0,360);

ПЕЧАТАТЬ:=Ra,Rc,Re1,Re2;

РАСЧЕТ:= СТАТИКА;

КОНЕЦ;

48

У тексті файлу вихідних даних крім невідомих реакцій додані

ють порівнювати завантаженість закріплень А та В із завантаженістю з’єднувального шарніра С. Результатом розв’язку є графіки залежності реакцій від кута нахилу сили F , які наведено на рис. 2.10–2.12.

Рисунок 2.10 – Графік залежності реактивного моменту

Рисунок 2.11 – Графік залежності реактивної сили у жорсткому закріпленні

49

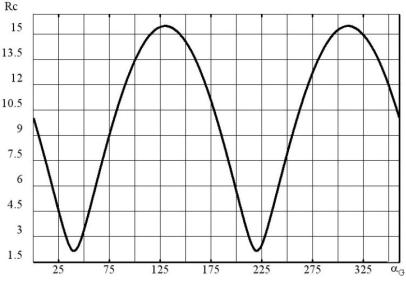
Якщо проаналізувати одержані результати, то, зокрема, можна з’ясувати умови, за яких з’єднувальний шарнір буде навантажений найменше. Згідно з результатами представленими на графіку (див. рис. 2.12), ці умови будуть виконуватись, якщо кут нахилу сили F дорівнює приблизно 40 або 220 .

Рисунок 2.12 – Графік залежності реакції у з’єднувальному шарнірі

2.3.1. Завдання для самостійної роботи. У табл. 2.4 і 2.5 запро-

поновано варіанти розрахункових схем та вихідні дані, згідно з якими необхідно визначити реакції опор складеної конструкції при дії плоскої системи сил.

Розв’язок необхідно провести у два етапи: спочатку визначити реакції аналітично, для заданого значення кута нахилу зосередженої сили (див. табл. 2.5). Після цього необхідно провести дослідження розподілу реакцій залежно від кута . Це дослідження необхідно проводити засобами ПК КіДиМ, користуючись прикладом тексту файлу вихідних даних. Графіки залежності реакцій необхідно побудувати в діапазоні [0, 360 ].

50