- •Методические указания к выполнению расчетно- графической работы «расчет электрической цепи синусоидального тока символическим методом» по курсу «электротехника и основы электроники»
- •Харьков нту "хпи" 2007
- •1. Общие требования
- •2. Порядок расчета символическим методом разветвленной линейной цепи синусоидального тока с одним источником эдс
- •3. Порядок расчета символическим методом разветвленной цепи со смешанным соединением активних и реактивних приемников синусоидального тока.
- •4. Задание для расчета
- •5. Пример расчета символическим методом разветвленной цепи со смешанным соединением приемников
- •Список литературы
- •Содержание
- •Методичні вказівки
- •61002, Харків, вул. Фрунзе, 21
4. Задание для расчета
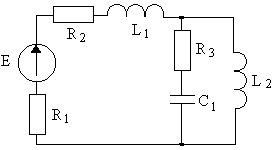
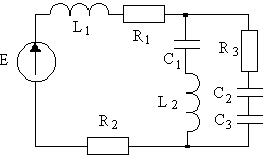
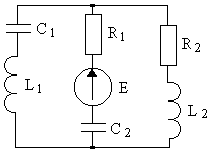
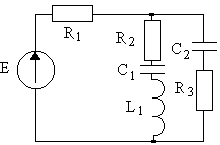
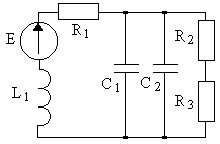
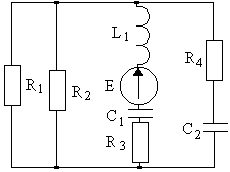
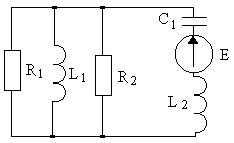
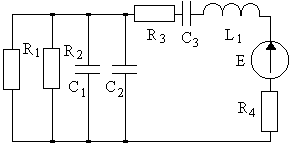
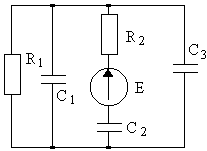
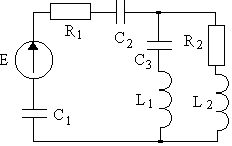
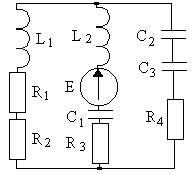
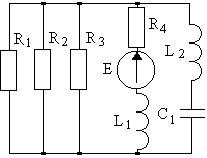
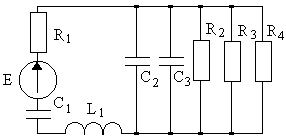
4.1. Варианты схем представлены в таблице 4.1.
Таблица 4.1
|
1 |
|
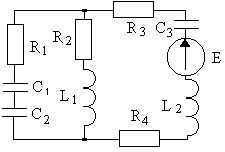
13 |
|
|
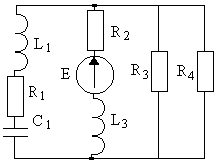
2 |
|
14 |
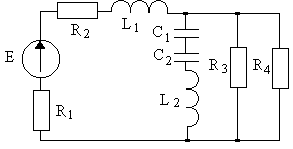
|
|
3 |
|
15 |
|
|
4 |
|
16 |
|
|
5 |
|
17 |
|
|
6 |
|
18 |
|
|
Продолжение таблицы 4.1 | |||
|
7 |
|
19 |
|
|
8 |
|
20 |
|
|
9 |
|
21 |
|
|
10 |
|
22 |
|
|
11 |
|
23 |
|
|
12 |
|
24 |
|
4.2. Варианты параметров схем представлены в таблице 4.2.
Таблица 4.2
|
№ |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
220 |
50 |
10 |
8.2 |
15 |
20 |
54.1 |
15 |
400 |
600 |
800 |
|
2 |
180 |
100 |
62 |
18 |
24 |
27 |
19.1 |
11.93 |
20 |
30 |
50 |
|
3 |
110 |
200 |
9.1 |
13 |
22 |
33 |
11.93 |
19.1 |
60 |
80 |
40 |
|
4 |
150 |
250 |
51 |
27 |
16 |
43 |
5.08 |
22.2 |
10 |
30 |
20 |
|
5 |
160 |
200 |
47 |
33 |
16 |
18 |
47.7 |
9.55 |
50 |
60 |
80 |
|
6 |
180 |
100 |
30 |
82 |
91 |
27 |
22.2 |
12.7 |
40 |
20 |
30 |
|
7 |
220 |
100 |
43 |
18 |
56 |
68 |
9.55 |
47.7 |
30 |
40 |
20 |
|
8 |
200 |
400 |
24 |
62 |
39 |
47 |
12.7 |
25 |
10 |
8 |
20 |
|
9 |
110 |
250 |
33 |
18 |
27 |
24 |
16 |
30 |
20 |
10 |
40 |
|
10 |
180 |
200 |
12 |
68 |
75 |
27 |
14 |
18 |
20 |
40 |
60 |
|
11 |
170 |
100 |
16 |
22 |
82 |
51 |
88 |
15 |
50 |
60 |
30 |
|
12 |
200 |
50 |
18 |
27 |
16 |
12 |
14 |
30 |
600 |
800 |
400 |
|
13 |
250 |
60 |
24 |
6.8 |
13 |
24 |
55 |
13 |
100 |
200 |
300 |
|
14 |
280 |
400 |
30 |
24 |
36 |
12 |
8.9 |
20 |
20 |
40 |
30 |
|
15 |
270 |
250 |
15 |
11 |
27 |
43 |
5.96 |
25 |
40 |
60 |
80 |
|
16 |
250 |
200 |
24 |
12 |
43 |
18 |
13.5 |
40 |
50 |
10 |
20 |
|
17 |
240 |
100 |
22 |
27 |
51 |
43 |
47.7 |
30 |
30 |
20 |
40 |
|
18 |
180 |
100 |
18 |
24 |
62 |
39 |
22.2 |
25 |
30 |
50 |
20 |
|
19 |
200 |
60 |
27 |
33 |
22 |
27 |
16 |
22.2 |
100 |
300 |
200 |
|
20 |
210 |
100 |
24 |
36 |
43 |
47 |
14 |
18 |
50 |
40 |
30 |
|
21 |
220 |
150 |
16 |
18 |
33 |
24 |
12 |
19 |
20 |
40 |
50 |
|
22 |
110 |
200 |
27 |
33 |
24 |
51 |
18 |
21 |
40 |
60 |
80 |
|
23 |
150 |
250 |
13 |
15 |
24 |
33 |
3.8 |
20 |
20 |
40 |
50 |
|
24 |
180 |
400 |
43 |
24 |
27 |
15 |
15 |
17 |
30 |
20 |
40 |
5. Пример расчета символическим методом разветвленной цепи со смешанным соединением приемников
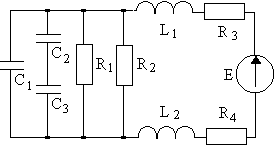
5.1. Задана цепь (рис.5.1) со следующими значениями параметров:
-
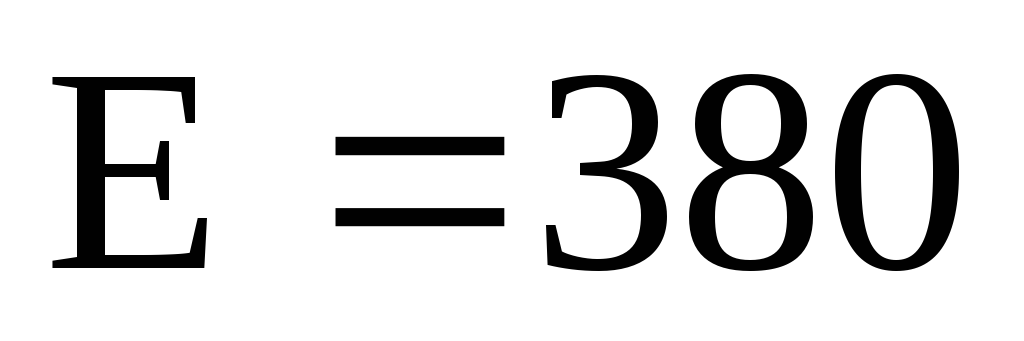 В,
В,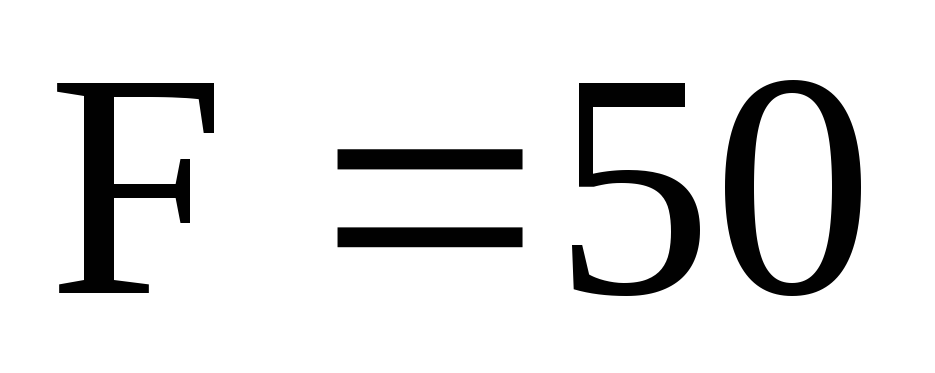 Гц,
Гц,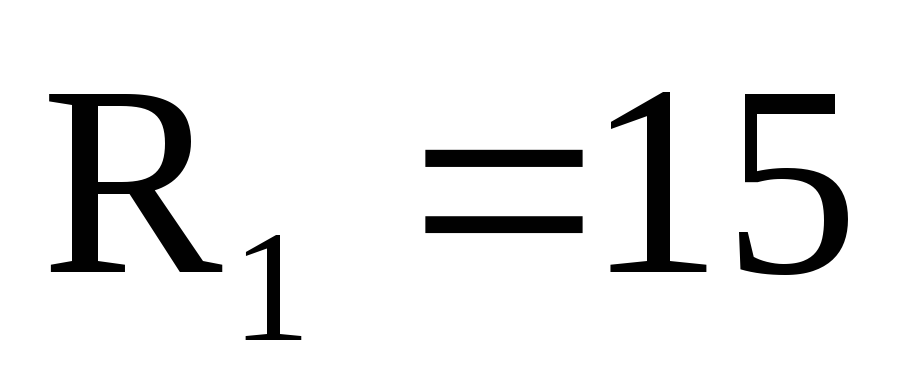 Ом,
Ом,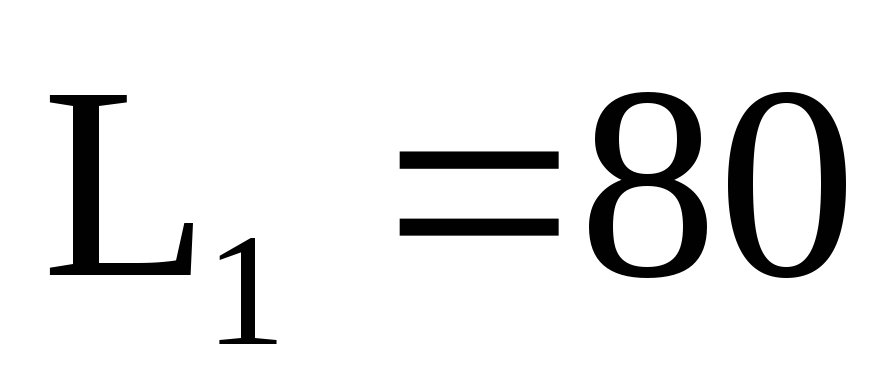 мГн,
мГн,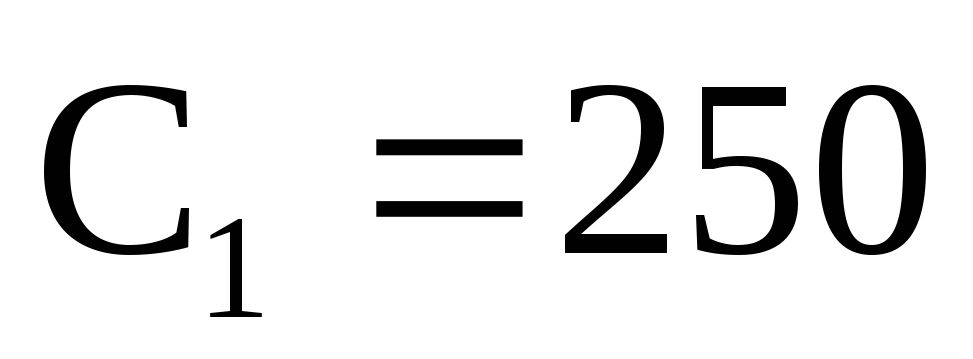 мкФ,
мкФ, Ом,
Ом, мГн,
мГн,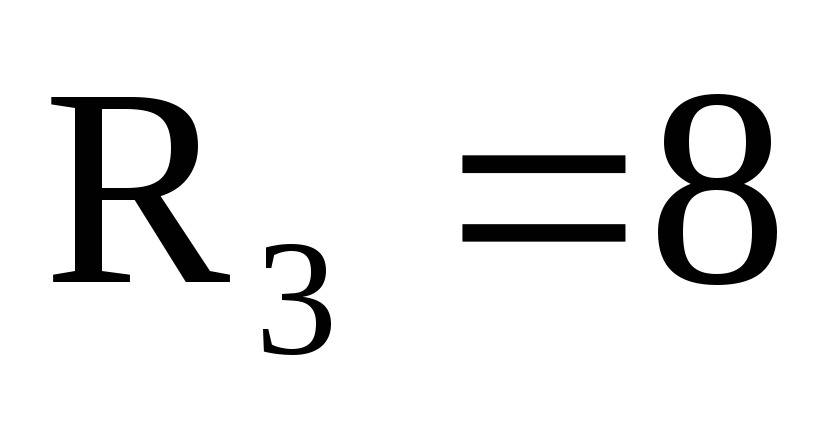 Ом,
Ом,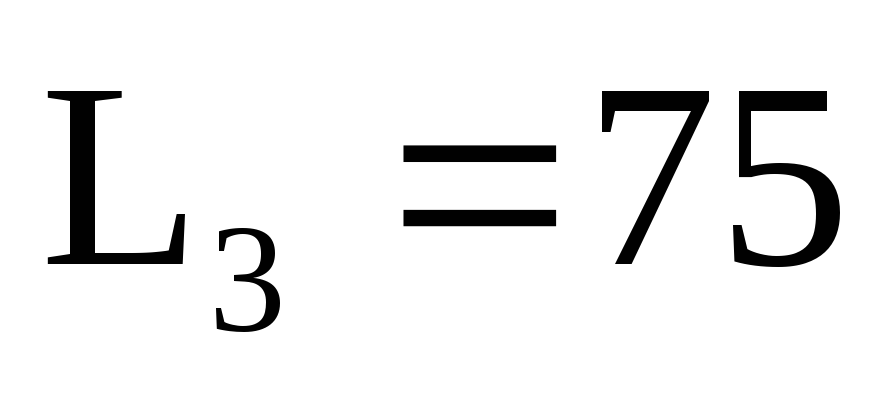 мГн,
мГн,
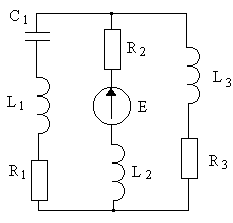
Рисунок 5.1 – Исходная цепь синусоидального тока
со смешанным соединением активных и реактивных приемников
5.2. Согласно требованиям п.2.1 настоящих методических указаний приводим заданную цепь к единой форме, соответствующей приведенным в п.2.1 требованиям (рис. 5.2).
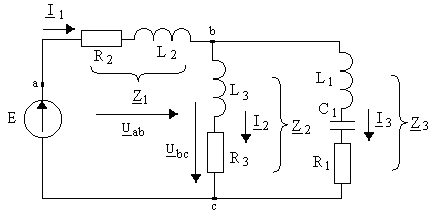
Рисунок 5.2 – Цепь, приведенная к единой топологии (форме)
5.3.
На преобразованной схеме рис.5.2
указываем условные положительные
направления токов
![]() ,
,
![]() ,
,
![]() и напряжений
и напряжений![]() ,
,
![]() .
.
5.4. Вычисляем модули сопротивлений всех реактивных приемников заданной схемы:
![]() Ом,
Ом,
![]() Ом,
Ом,
![]() Ом,
Ом,
![]() Ом.
Ом.
Округляем полученные значение реактивных сопротивлений до двух верных значащих цифр:
![]() Ом,
Ом,
![]() Ом,
Ом,
![]() Ом,
Ом,
![]() Ом.
Ом.
5.5. Вычисляем комплексы полных сопротивлений ветвей цепи:
![]() Ом,
Ом,
![]() Ом,
Ом,
![]() Ом.
Ом.
5.6. Вычисляем комплекс и модуль полного эквивалентного сопротивления заданной цепи
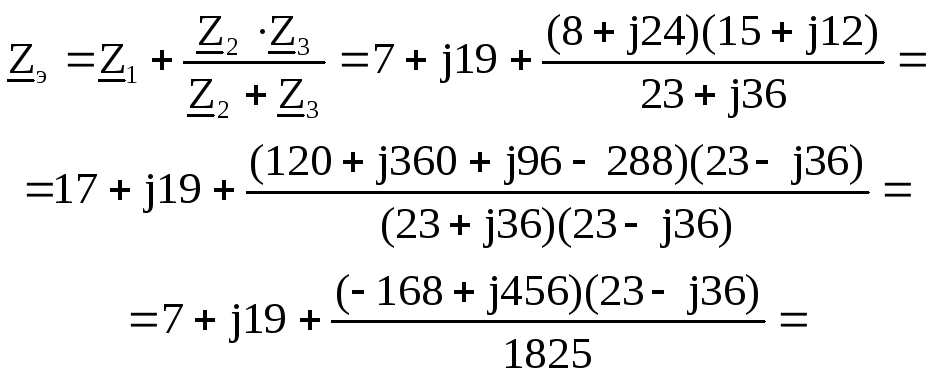
![]()

![]()
![]()
![]()
![]()
![]() Ом.
Ом.
5.7. Изображаем эквивалентную схему замещения цепи (рис. 5.3).
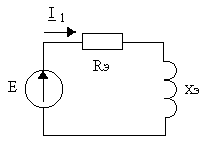
Рисунок 5.3 – Эквивалентная схема замещения цепи
5.8.
Вычисляем комплекс, модуль действующего
значения и амплитудное значение тока
в цепи источника ЭДС ![]() –
– ![]() в соответствии с законом Ома в комплексной
форме:
в соответствии с законом Ома в комплексной
форме:
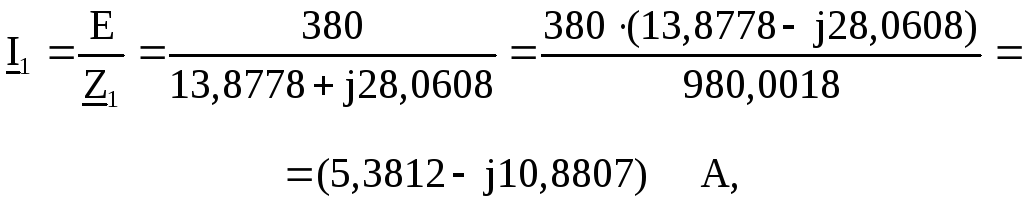
![]() А,
А,
![]() А.
А.
Мнимая часть
комплекса тока ![]() имеетзнак “–“,
что соответствует активно-индуктивному
характеру эквивалентной схемы замещения
(рис. 5.3).
имеетзнак “–“,
что соответствует активно-индуктивному
характеру эквивалентной схемы замещения
(рис. 5.3).
5.9.
Вычисляем повторно модуль тока ![]() в
соответствии с законом Ома для модулей:
в
соответствии с законом Ома для модулей:
![]() Ом.
Ом.
Относительная
погрешность вычисления модуля тока ![]() cоставляет
cоставляет
![]() .
.
5.10.
Вычисляем значение угла сдвига фазы в
градусах между вектором ЭДС Е и вектором
тока
![]() в цепи источника
в цепи источника
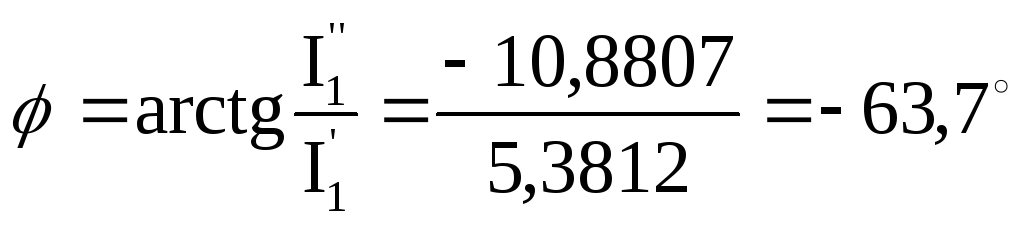 .
.
Знак “–“ в этом случае также соответствует активно-индуктивному характеру эквивалентной схемы замещения (рис. 5.3).
5.11.
Вычисляем комплексы, модули действующих
значений и амплитудные значения
напряжений
![]() и
и![]() в соответствии
с законом Ома и вторым законом Кирхгофа
в комплексной форме.
в соответствии
с законом Ома и вторым законом Кирхгофа
в комплексной форме.
![]() В,
В,
![]() В,
В,
![]() В,
В,![]()
![]()
![]() В,
В,
![]() В.
В.
5.12.
Вычисляем комплексы, модули действующих
значений и амплитудные значения токов
![]() ,
,
![]()
![]() А,
А,
![]() А,
А,
![]() А,
А,
![]() А,
А,
![]() А,
А,
![]() А.
А.
5.13 Выполняем проверку решения в соответствии с первым законом Кирхгофа в комплексной форме для узла “b”:
![]()
![]()
![]() ;
;
![]()
![]()
![]() .
.
В
данном случае условие проверки выполняется
с абсолютной погрешностью
![]() .
.
5.14. Вычисляем
комплекс полной мощности, отдаваемой
источником ЭДС
![]() во
внешнюю цепь.
во
внешнюю цепь.
![]()
![]() Bт,
Bт,
![]() ВАр.
ВАр.
Наличие
действительной и положительной мнимой
частей в выражении для
![]() соответствует активно-индуктивному
характеру эквивалентной схемы замещения
цепи (рис.5.3).
соответствует активно-индуктивному
характеру эквивалентной схемы замещения
цепи (рис.5.3).
5.15. Вычисляем комплексы полных мощностей, потребляемых в отдельных ветвях цепи:
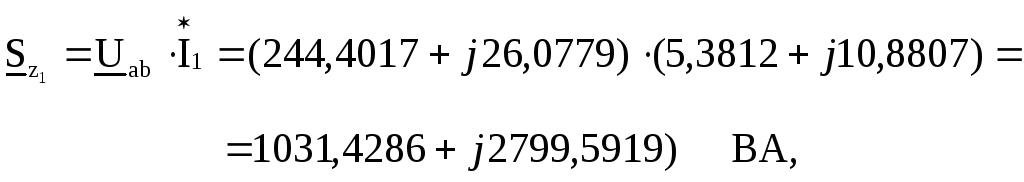
![]() Вт,
Вт,
![]() ВАр.
ВАр.
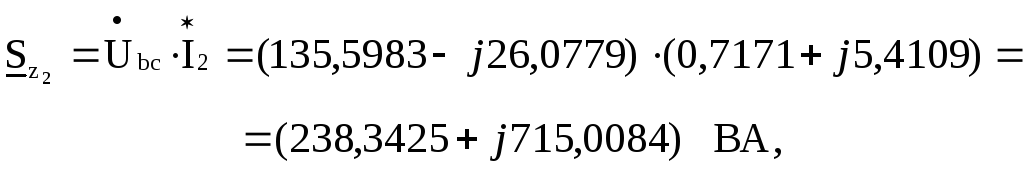
![]() Вт,
Вт,
![]() ВАр.
ВАр.
![]()
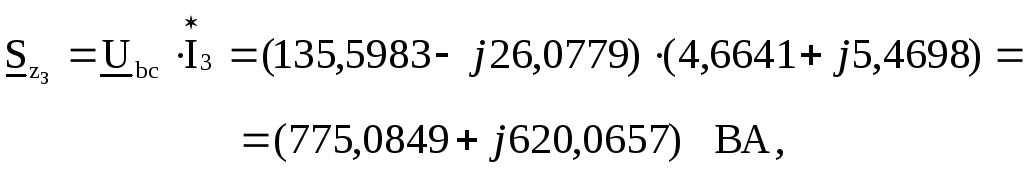
![]() Вт,
Вт,
![]() Ар.
Ар.
Значение
действительной и положительной мнимых
частей комплексов мощностей
![]() ,
,![]() ,
,
![]() соответствуют активно-индуктивному
характеру ветвей
соответствуют активно-индуктивному
характеру ветвей
![]() ,
,
![]() ,
,
![]() .
.
5.16. Проверяем выполнение баланса активной и реактивной мощностей в заданной цепи
![]() ;
;
![]() ;
;
![]()
![]() ;
;
![]()
![]()
В
данном случае баланс активной и реактивной
мощностей выполняется с абсолютной
точностью
![]() .
.
5.17.
Строим векторную диаграмму (рис. 5.4) в
единой системе координат на комплексной
плоскости для токов
![]() ,
,
![]() ,
,
![]() ,
ЭДС
,
ЭДС ![]() и напряжений
и напряжений
![]() ,
,
![]() для чего:
для чего:
а)
исходя из значения максимальной проекции
векторов токов
![]() ,
,
![]() ,
,
![]() на любую из осей комплексной плоскости
(
на любую из осей комплексной плоскости
(![]() ),
выбираем масштаб тока
),
выбираем масштаб тока![]()
![]() ;
;
б)
исходя из значения максимальной проекции
векторов ЭДС ![]() и напряжений
и напряжений
![]() и
и
![]() на любую из осей комплексной плоскости
(
на любую из осей комплексной плоскости
(![]() ),
выбираем масштаб напряжения
),
выбираем масштаб напряжения![]()
![]() ;
;
в) откладываем в выбранных масштабах для каждого вектора токов и напряжений их проекции (с учетом знака) на оси действительных и мнимых чисел, определяя их длины следующим образом:
![]() мм,
мм,
![]()
![]() мм,
мм,
![]() мм,
мм,
![]() мм,
мм,
![]() мм,
мм,
![]() мм,
мм,
![]() мм,
мм,
![]() ,
,
![]() мм,
мм,
![]() мм,
мм,
![]() мм.
мм.
5.18.
Построив векторную диаграмму, убеждаемся,
что на ней выполняется первый закон
Кирхгофа в векторной форме для узла
“b”,
т.е. вектор
![]() равен
сумме векторов
равен
сумме векторов
![]() и
и
![]() ,
а также выполняется
второй закон Кирхгофа для контура abc,
т.е. вектор
,
а также выполняется
второй закон Кирхгофа для контура abc,
т.е. вектор ![]() равен сумме векторов
равен сумме векторов
![]() и
и
![]() .
.
![]()
 ;
;
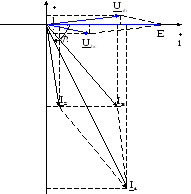
Рисунок 5.4 – Векторная диаграмма
5.19.
Убеждаемся, что на векторной диаграмме
вектор тока
![]() отстает
от вектора напряжения
отстает
от вектора напряжения
![]() на угол
на угол
![]() ,
векторы
,
векторы
![]() и
и
![]() отстают от вектора напряжения
отстают от вектора напряжения
![]() на углы
на углы
![]() ,
,![]() ,
что соответствует активно-индуктивному
характеру ветвиab
и двух параллельных ветвей, заключенных
между узлами “ b”
и “c”.
,
что соответствует активно-индуктивному
характеру ветвиab
и двух параллельных ветвей, заключенных
между узлами “ b”
и “c”.
5.20. Составляем итоговую таблицу расчетов (табл. 5.1).
Таблица 5.1
-
Пара-
метр
Раз-
мер-
ность
Значение
параметра
Пара-
метр
Раз-
мер-
ность
Значение
параметра
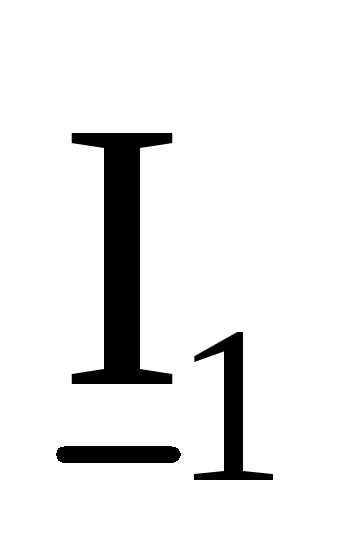
А
5,3812-j10,8807
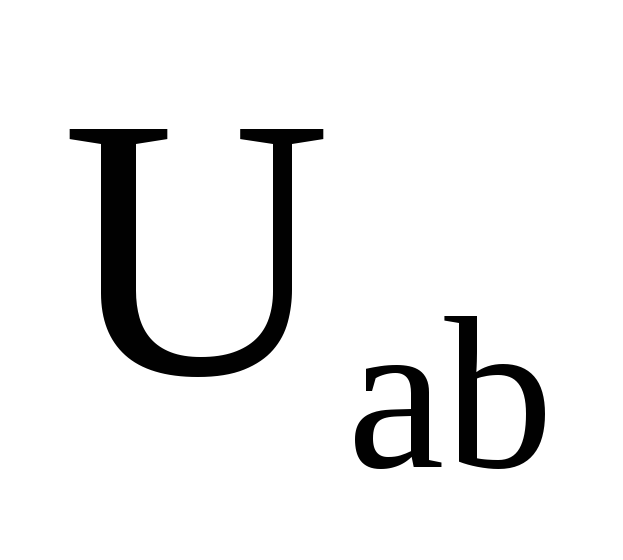
B
245,7816
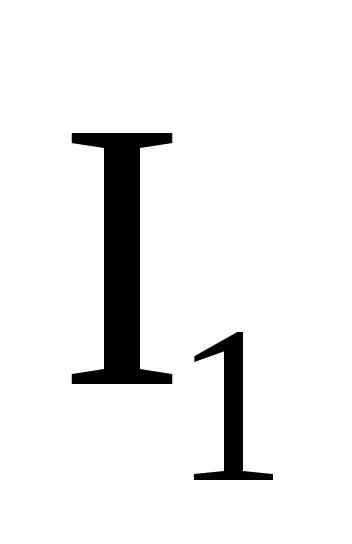
А
12,1387
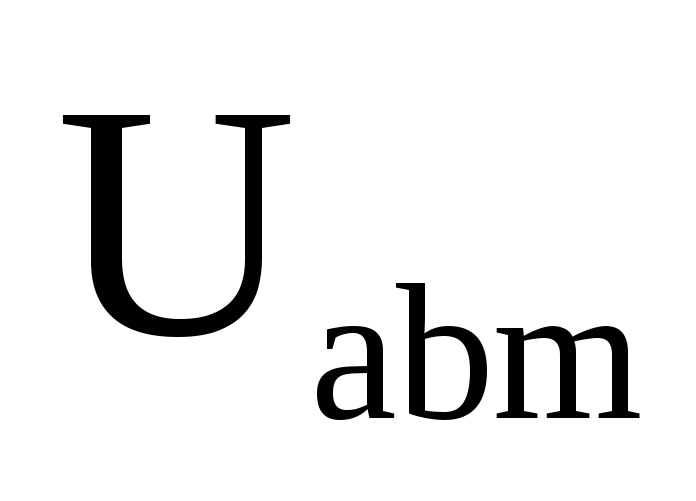
B
347,5877
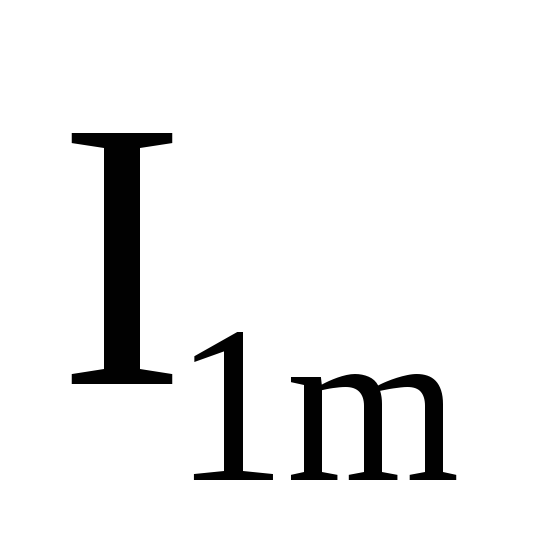
А
17,1667
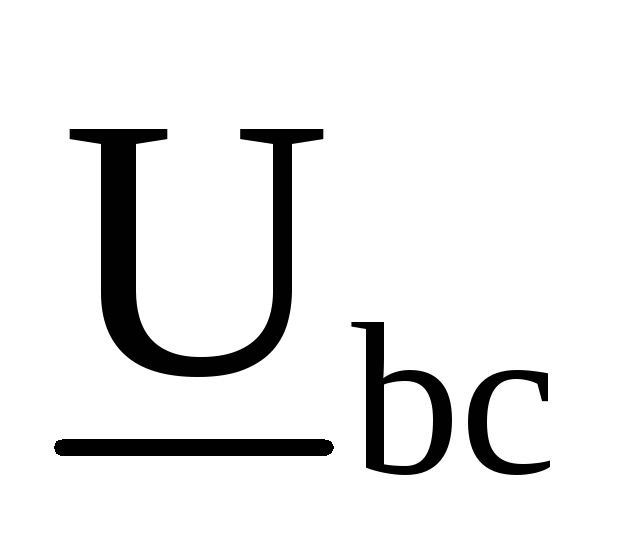
B
135,5983-j26,0779
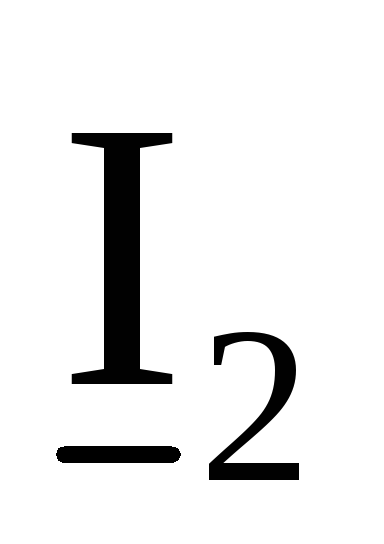
А
0,7171-j5,4109
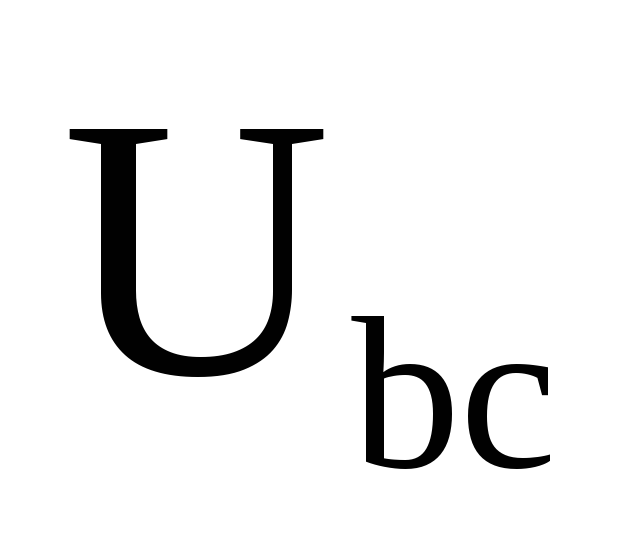
B
138,0831

А
5,4582
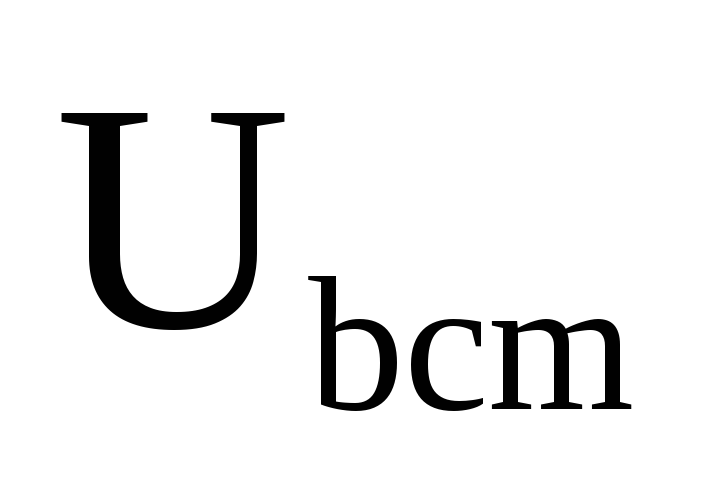
B
195,2790

А
7,7191

град
63,7
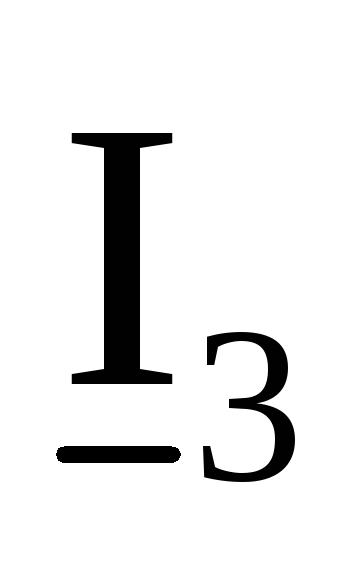
А
4,6641-j5,4638


ВА
2044,8560+j4134,6660
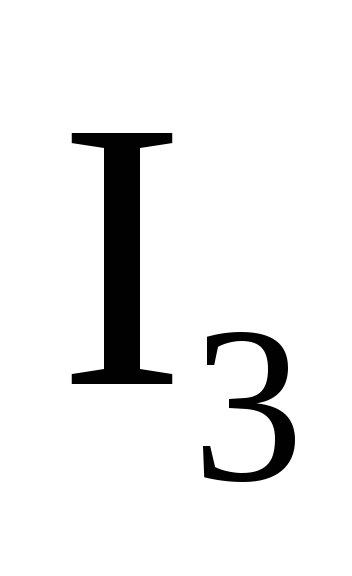
А
7,1883
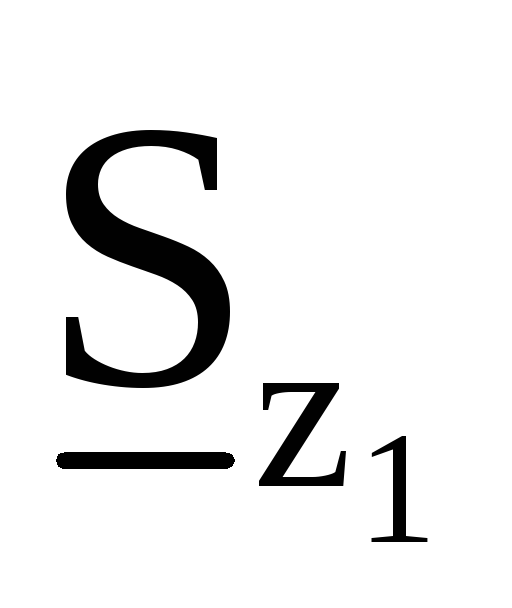
ВА
1031,4286+j2799,5919
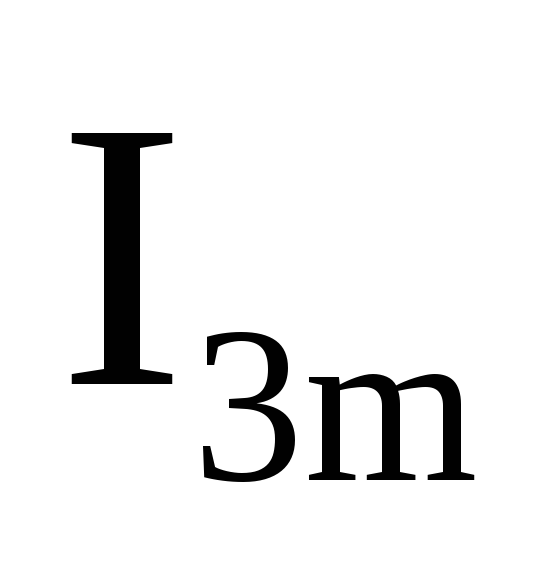

А
10,1659
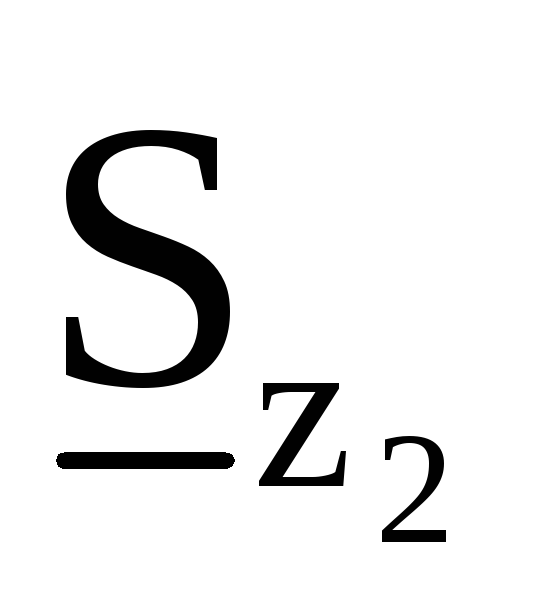
ВА
238,3425+j715,0084
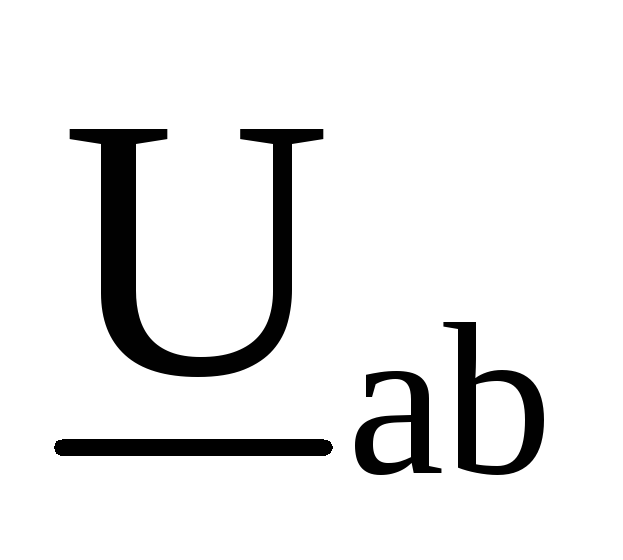
А
244,4017-j26,0779

ВА
775,0849+j620,0657