
- •Министерство образования и науки Российской Федерации
- •Содержание
- •Введение
- •Нагрузки на панель перекрытия
- •12. Расчет на прочность по нормальному сечению в стадии
- •Расчет прочности панели перекрытия по сечениям наклонным к ее продольной оси
- •Расчет панели перекрытия по предельным состояниям второй группы (по трещиностойкости и деформативности)
- •Расчет панели перекрытия по раскрытию трещин от эксплуатационных нагрузок
- •Расчет на образование трещин
- •Расчет панели перекрытия по деформативности (прогибам) от эксплуатационных нагрузок
- •С учетом веса самой конструкции
- •Расчет монтажных петель панели перекрытия
- •Расчет трех пролетного неразрезного ригеля Данные для расчета.
- •Расчет прочности ригеля в нормальных сечениях
- •Расчет ригеля на прочность по сечениям наклонным к его продольной оси
- •Расчет монтажных и транспортных воздействий на ригель
- •Расчет монтажных петель
- •Расчет стыка сборных элементов ригеля
- •Расчет сборной железобетонной колонны многоэтажного здания.
- •Нагрузки от покрытия на колонну первого этажа
- •Расчет на прочность колонны первого этажа
- •Расчет и конструирование консолей колонны
- •Конструирование стыков колонн
- •Расчет сборных элементов многоэтажной колонны на воздействия в период транспортирования и монтажа
- •Расчет трехступенчатого центрально-нагруженного фундамента Сбор нагрузок на фундамент
- •Расчет на прочность и раскалывание фундамента
- •Заключение
- •Литература
Расчет трех пролетного неразрезного ригеля Данные для расчета.
Ригель
без предварительного натяжения рабочей
арматуры. Бетон тяжелый класса Б
20, (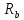 =
11,5 мПа).
для рабочей продольной арматуры примем
сталь класса А
400
(
=
11,5 мПа).
для рабочей продольной арматуры примем
сталь класса А
400
(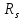 = 355 мПа),
для поперечных стержней примем сталь
класса А
240
(
= 355 мПа),
для поперечных стержней примем сталь
класса А
240
(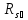 =170 мПа),
Размер всех пролетов в разбивочных осях
равен 7,1
м.
Шаг колонн 7,1
м.
=170 мПа),
Размер всех пролетов в разбивочных осях
равен 7,1
м.
Шаг колонн 7,1
м.
Определим предварительно размеры прямоугольного сечения ригеля из выражения:
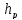 =(
=(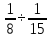 )•l
(м)
(76)
)•l
(м)
(76)
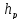 =
=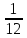 •l=
•l=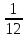 •7,1=0,5916
(м)
•7,1=0,5916
(м)
Окончательно
принимаем высоту ригеля 0,6 м (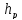 =0,6
м).
=0,6
м).
Ширину сечения ригеля предварительно определим из выражения:
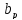 =(0,3
=(0,3
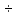 0,4)
0,4)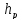 (77)
(77)
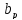 =
0,4
=
0,4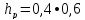 =0,24
(м)
=0,24
(м)
Окончательно
примем ширину ригеля 0,25 м
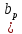 =0,25
м).
=0,25
м).
Определим нагрузку от собственного веса ригеля из выражения:
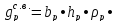 (10)
Нм
(78)
(10)
Нм
(78)
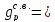 0,25•0,6•2500•(10)
= 3750 (
0,25•0,6•2500•(10)
= 3750 (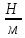 )=3,75
(
)=3,75
(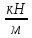 ).
).
Определим грузовую площадь, с которой нагрузки от конструкции пола и веса плит перекрытия действуют на ригель.

 Рис.
10. Грузовая площадь, на ригель
Рис.
10. Грузовая площадь, на ригель
Постоянную погонную расчетную нагрузку на ригель от веса конструкции пола, от веса панели перекрытия и собственного веса ригеля определим из выражения:
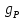 =
=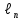 •(
•(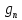 +
+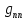 )•
)•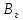 +
+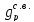 (79)
(79)
где:
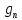 -
нагрузка
от конструкции пола (
-
нагрузка
от конструкции пола (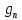 =2,043
кПа)
(табл.
1 стр.7);
=2,043
кПа)
(табл.
1 стр.7);
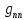 -
нагрузка от панели перекрытия (
-
нагрузка от панели перекрытия (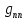 =6,96
кПа)
(табл.
1 стр.7);
=6,96
кПа)
(табл.
1 стр.7);
 -
ширина
грузовой площади (
-
ширина
грузовой площади (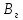 =
6 м).
=
6 м).
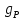 =0,95•[(2.043+3,861)•7,1+3,75]
= 43,38498
=0,95•[(2.043+3,861)•7,1+3,75]
= 43,38498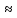 43,4
(
43,4
(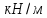 ).
).
Временную погонную расчетную нагрузку на ригель определим из выражения:
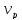 =
=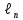 •
v•
•
v•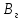 (80)
(80)
где – v- временная полная расчетная нагрузка на единицу площади панели перекрытия (v = 2,400 кПа, табл. 1, стр. 7).
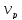 =0,95•7,1•5,4=36,4
=0,95•7,1•5,4=36,4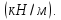
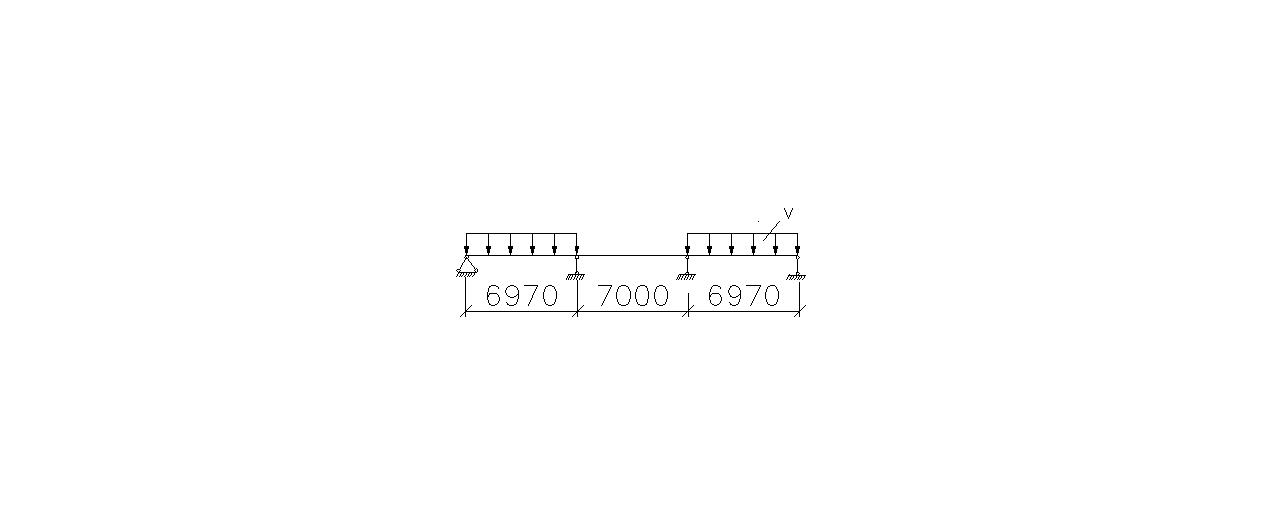
Определим расчетные пролеты трех пролетного неразрезного ригеля.
Длина опоры ригеля первого и третьего пролетов на несущие стены здания равна 0,2 м. Тогда расчетное значение первого и третьего пролетов составит величину:
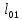 =
=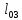 =
7,1–
=
7,1–
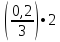 =6,966
=6,966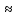 6,97м
6,97м
Расчетный
второй пролет
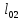 =7
м.
=7
м.
Расчет значений изгибающих моментов и поперечных сил от внешних усилий выполним в табличной форме.
|
№ |
Схемы загружения |
Изгибающие моменты (кНм) |
Поперечные силы (кН) | ||||||||||||||
|
|
|
|
|
|
|
|
| ||||||||||
|
1. |
|
0,08•43,4• • =168,67 |
0,025•43,4•
=53,16 |
168,67 |
-0,1•43,4•
=-212,66 |
-212,66 |
0,4•43,4• •6,97= =120,99 |
-0,6•43,4• •6,597= =-181,49 |
0,5•43,4• •6,7=
=151,9 | ||||||||
|
2. |
|
0,1•36,4•
=176,83 |
0,05•36,4•
|
176,83 |
-0,05•36,4• • =-89,18 |
=-89,18 |
0,45•36,4• •6,97= =114,16 |
0,55•36,4• •6,97= =139,53 |
0 | ||||||||
|
3 |
|
-0,025•36,4• • =-44,200 |
0,075•36,4• •
=133,77 |
-44,20 |
-0,05•36,4• • =-89,18 |
=-89,18 |
-0,05•36,4• •6,97= =-12,68 |
-0,05•36,4• •6,97= =-12,68 |
0,536,4• •7=
=127,4 | ||||||||
|
4 |
|
245,66 |
-240,58 |
23,54 |
-0,117•36,4• • -208,68 |
-0,033• 36,4• =-58,85 |
0,383•36,4• •6,97= =97,17 |
-0,617•36,4• •6,97= =-156,53 |
0,583•36,4• •7=
=148,54 | ||||||||
|
Сочетание 1+2 |
345,5 |
-36,02 |
345,5 |
-301,12 |
-301,12 |
235,15 |
-41,96 |
151,9 | |||||||||
|
Сочетание 1+3 |
124,47 |
186,93 |
124,47 |
-301,12 |
-301,12 |
108,31 |
-194,17 |
279,3 | |||||||||
|
Сочетание 1+4 |
464,33 |
187,42 |
192,21 |
-421,34 |
-271,51 |
218,66 |
-338,02 |
300,44 | |||||||||
|
Невыгоднейшее сочетание |
464,33 |
-36,02 |
345,5 |
-421,34 |
-301,12 |
108,31 |
-338,02 |
151,9 | |||||||||
Расчет значений изгибающих моментов и поперечных сил от внешних усилий, действующих на ригель
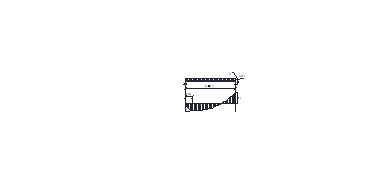
Рис. 11. К определению изгибающих моментов в первом пролете от 4 схемы загружения
Из статического условия равновесия определим значение реакции опоры В.
Σ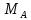 = 0.
= 0.
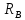 •
•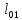 +
+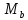 -
-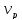 •
•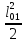 = 0(81)
= 0(81)
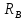 =
=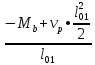 (82)
(82)
 =
=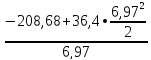 =126,44
кН
=126,44
кН
Σ = 0
= 0
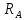 •
•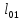 +
+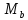 -
-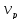 •
•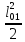 = 0(83)
= 0(83)
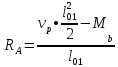 (84)
(84)
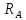 =
=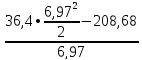 =156,79кН
=156,79кН
Определим
значение максимального изгибающего
момента от четвертой схемы загружения
на расстоянии
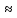 0,4
0,4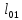 от
опоры «А».
от
опоры «А».
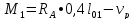 •
•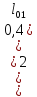 (85)
(85)
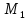 =110,11•0,4•6,97-36,4•
=110,11•0,4•6,97-36,4•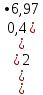 =136,39
кНм
=136,39
кНм
Определим максимальное значение изгибающего момента во втором пролете от четвертой схемы загружения. Максимальное значение изгибающего момента расположено в середине второго пролета.

Рис. 12. К определению изгибающих моментов во втором пролете от 4 схемы загружения
Из
уравнений статики определим опорные
реакции и значение максимального
пролетного момента во втором пролете
от четвертой схемы загружения (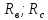 и
и
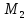 ).
).
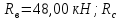 =34,2
кН;
=34,2
кН;
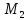 =24,65
кНм.
=24,65
кНм.

Рис. 13. К определению изгибающих моментов в третьем пролете от 4 схемы загружения
Из
уравнений статики определим опорные
реакции и значение максимального
пролетного момента в третьем пролете
пролете (на расстоянии
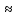 0,4
0,4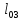 от
опоры «С») от четвертой схемы загружения
(
от
опоры «С») от четвертой схемы загружения
(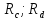 и
и
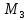 ).
).
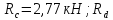 =-2,77
кН;
=-2,77
кН;
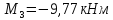 ).
).
Новые значения опорных изгибающих моментов на промежуточных опорах:
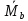 =
=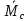 =421,34-
421,34•0,3=294,94 кНм
=421,34-
421,34•0,3=294,94 кНм
Для треугольной эпюры протяженностью от опоры «А» до опоры «С» , вершина которой находится под опорой «В», значение изгибающего момента равно:
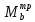 =
=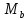 -
-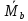 (86)
(86)
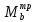 =421,34-294,94=126,4
кНм
=421,34-294,94=126,4
кНм
Значения ординат в треугольной эпюре в сечениях с максимальными значениями изгибающих моментов в первом и втором пролетах определим по правилам подобия треугольников.
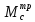 =
=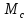 -
-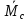
где
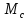 -
табличное
значение сочетания (1+4), а
-
табличное
значение сочетания (1+4), а
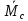 - новое значение.
- новое значение.
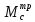 =271,51-294,94=-23,43
кНм
=271,51-294,94=-23,43
кНм
Значения ординат треугольных эпюр под опорами «В» и «С» определим из выражения:
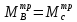 =301,12-294,94=6,18
кНм
=301,12-294,94=6,18
кНм
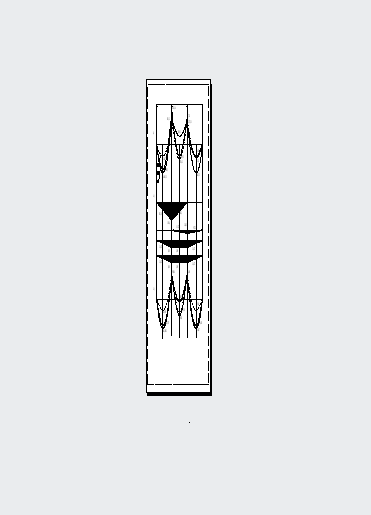
Рис 14 Эпюры изгибающих моментов.
а) эпюры в предположении упругих свойств бетона; б) эпюры пластических свойств бетона; в) эпюры с учетом упруго пластических свойств бетона.
Для изгибающего момента на опоре «В» принимаем значение по грани колонны определяемое из выражения:
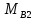 =
=
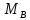 -
-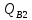 •
•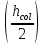 (87)
(87)
где:
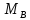 =294,94
кНм;
=294,94
кНм;
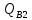 =41,96
кН
–
значение поперечной силы на опоре «В»
от сочетания (1+2);
=41,96
кН
–
значение поперечной силы на опоре «В»
от сочетания (1+2);
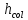 -
ширина колонны (примем предварительно
ширину колонны 0,4 м).
-
ширина колонны (примем предварительно
ширину колонны 0,4 м).
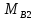 =294,94-41,96•
=294,94-41,96•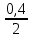 =286,55
кНм
=286,55
кНм
Для расчета прочности ригеля по наклонным сечениям к его продольной оси примем максимальные значения поперечных сил.
На
опоре «А»
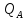 =108,31
кН.
=108,31
кН.
На
опоре «В» со стороны первого пролета
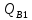 =338,02
кН.
=338,02
кН.
На
опоре «В» со стороны второго пролета
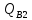 =151,9
кН.
=151,9
кН.

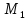
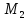
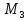
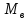
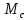
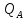
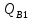
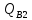
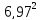 =
=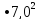 =
=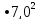 =
=
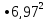 =
=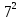 =89,18
=89,18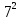 =
=
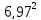 =
=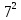 =
= =
=
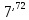 =
=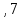 =
=