
3 Решение задач
Производство специализируется на выпуске напитков "Sprite " . Воспользуемся выше перечисленными методами оптимизации, чтобы оптимизировать процессы производства и распределения.
Первым делом для производителя это создание самого производственного процесса , то есть помещение , внутренние работы , производство , реклама . Чтобы решить эти объемные вопросы в ускоренном режиме и с наименьшими затратами, решим следующую задачу сетевого планирования , чтобы планы наших работ были выполнены эффективно и вовремя.
1)Составимтаблицу последовательности работ и времени их выполнения.

Рисунок 1 .Таблица последовательности работ и времени их выполнения.
1.2) Строим диаграмму Ганта и по диаграмме определяются события проекта.

Рисунок 2 . Диаграмма Гранта
1.3) Строим сетевой график для определения кратчайшего пути выполнения работ .
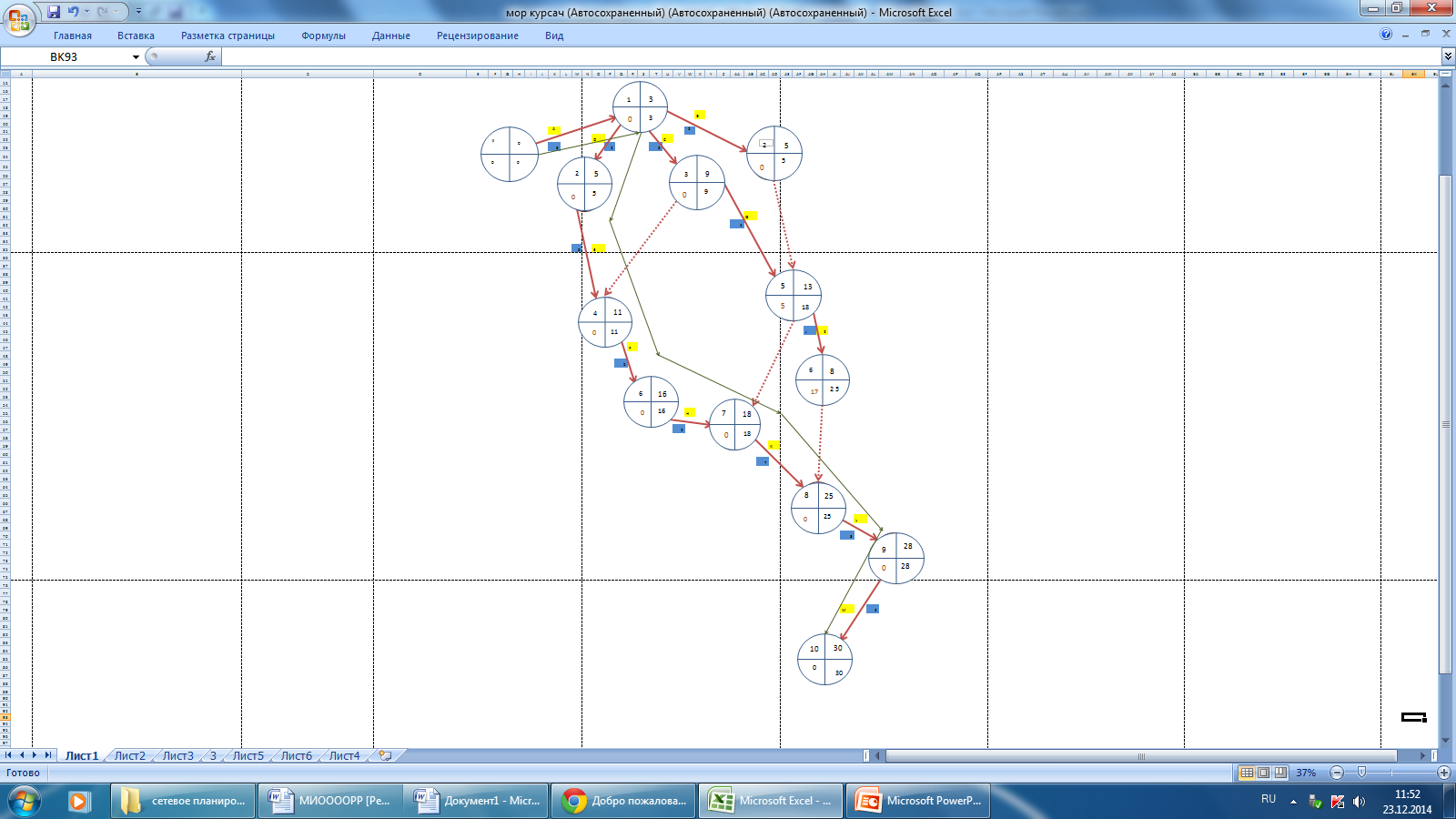
Рисунок 3. Сетевой график.
Из сетевого графика можно сделать вывод , что в общем план выполнения работ оптимален и требует мало времени для полноценного его выполнения .
2) Для определения оптимального выпуска продукта решим следующие задачи и определим какие виды напитков выгодно производить , а какие нет?Для ответа на поставленные вопросы решим следующую задачу :

Рисунок 4 . Задача оптимизации

Рисунок 5 . Линейная и двойственная задача оптимизации .
Решив двойственную задачу можно сделать вывод , что выгодно производить продукт А и В , продукт Б не выгоден на производство .

Рисунок 6 . Оптимизация выпуска продукции с помощью Симплекс метода.
Так же можно сделать вывод , что симплекс метод продукт А является самым эффективным продуктом для продажи , по степени убывания по эффективности и ликвидности будет продукт Б , продукт В не является ликвидным и оптимальным для выпуска .
3 )Следующий шаг - это реализация продукта.
Торговые агенты разных гипермаркетов заинтересованы в закупке нового вида напитка Sprite. И при этом торговому агенту необходимо знать оптимальный размер заказа , совокупный издержки и т.д., чтобы минимизировать свои затраты и максимизировать прибыль. Для ответа на эти вопросы решим следующие задачи :

Рисунок 7 . Задача оптимизации закупки и управления запасами.
Гипермаркет «Авангард» получит прибыль , если будет пользоваться оптимальным заказом товаров , значения которых приведены на рисунке 7 . Стоит обратить внимание на то , что если заказывать больше продуктов , то затраты на издержки не изменятся.
4 ) Следующий этап производства - это перевозки продукта .Теперь , зная потребности закупщиков , нужно решить задачу транспортировки продукта так , чтобы наши затраты на перевозки были минимальными и при этом , чтобы потребности заказчиков были удовлетворены. Для определения транспортировки продукта решим следующую задачу :

Рисунок 8 . Постановка задачи ТЗ.

Рисунок 9 . Оптимальный план перевозок разными методами .
Из всех составленных планов транспортировки продукта будет план , который составлен по минимальному элементу , стоимость по – минимуму обойдется в 10360д.ед.

Рисунок
10 . Выбор оптимального плана транспортировки
продукции. 
Рисунок 11 . Метод потенциалов .
Метод потенциалов так же подтвердил , что самым оптимальным планом перевозок будет план , который был составлен по минимальному элементу. Стоимость транспортировки с минимумом будет составлять 10360 д.ед.
ЗАКЛЮЧЕНИЕ
Проведя анализ оптимальности производства, можно сделать вывод, что используя разные методы оптимизации можно выбрать экономические решения , которые позволят снизить затраты на производство и реализацию продукции. Каждый метод актуален в любое время , когда нужны оптимальные решения и эффективные использования сырья , а так же план с минимальными затратами перевозок . Выбирая продукты на продажу также можно пользоваться методами управления запасами , чтобы максимизировать прибыль . Методы оптимальных решении обновляются и используются почти во всех сферах общественной жизни.
СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ
1 Акулич И.Л. Математическое программирование в примерах и задачах. – М.: Высшая школа, 1986.
2 Ашманов С.А. Линейное программирование. М.: Наука, 1981.
3 Юдин Д.Б., Гольдштейн Е.Г. Линейное программирование. - М.: Физматлит, 1963.
4 Васильев Ф.П., Иваницкий А.Ю. Линейное программирование. - М.: Факториал , 2003.
5 Саврасов Ю.С. Оптимальные решения. - Радио и связь, 2000
6 Литовка Ю.В. Получение оптимальных проектных решений и их анализ с использованием математических моделей / Ю.В.Литовка. – Тамбовский Государственный Технический университет, 2006
7 Кузнецов Ю.Н., Кузубов В.И., Волощенко А.Б. Математическое программирование. – М.: Высшая школа, 1980.
8 Соловьев В. И. Методы оптимальных решений: Учебное пособие. М.: Финансовый университет, 2012.
9 Палий И.А. Линейное программирование. Учебное пособие – Москва, 2008
10 Соколов А.В., Токарев В.В. Методы оптимальных решений. Том 1. Общие положения. - М.: ФИЗМАТЛИТ, 2012
11 Кузнецов А. В., Сакович В. А., Холод Н. И. Высшая математика. Математическое программирование. Учебник. 3-е изд. – Лань 2010
12 Браверман Э.М. Математические модели планирования и управления в экономических системах /Э.М.Бравеман. - М.: Наука, 1976.
