
- •V2: де 59 - Действительная и мнимая части комплексного числа
- •V2: де 73 - Вариационный ряд. Мода и медиана
- •V2: де 14 – Векторные пространства. Коллинеарность векторов.
- •V1: Векторный анализ
- •V2: де 11 - Векторные пространства. Линейные операции над векторами
- •V2: де 63 - Вероятность события а
- •V2: де 72 - Полигон частот, гистограмма
- •V2: де 51 - Графы
- •V2: де 49 – Булевы функции
- •V2: де 67 - Закон распределения дискретной случайной величины
- •V2: де 53 - Способы решения обыкновенных дифференциальных уравнений первого порядка
- •V2: де 54 - Дифференциальные уравнения, допускающие понижение порядка
- •V2: де 39 - Интегральное исчисление функции одной переменной. Приложения определенного интеграла
- •V2: де 31 - Введение в анализ. Окрестность точки
- •V2: де 61 - Модуль и аргумент комплексного числа
- •V2: де 60 - Комплексно сопряженные числа
- •V2: де 58 - Арифметические действия над комплексными числами
- •V2: де 24 - Аналитическая геометрия. Приведение уравнения кривой второго порядка к каноническому виду
- •V2: де 4 – Линейные отображения. Линейные операции над матрицами
- •V2: де 55 - Решение линейных неоднородных уравнений со специальной правой частью
- •V1: Дискретная математика
- •V2: де 47 - Множества
- •V2: де 44 – Функциональный анализ. Отображение множеств
- •V2: де 66 - Полная группа событий
- •V2: де 29 - Введение в анализ. Предел функции на бесконечности
- •V2: де 35 - Дифференциальное исчисление функции одной переменной. Производные высший порядков
- •V2: де 32 - Дифференциальное исчисление функции одной переменной. Производная
- •V2: де 6 - Линейные отображения. Определители второго порядка
- •V2: де 50 – Теория алгоритмов
- •V2: де 76 - Оценки параметров распределения
- •V2: де 2 – Линейные отображения. Транспонирование матриц.
- •V2: де 5 - Линейные отображения. Умножение матриц
- •V2: де 22 - Аналитическая геометрия. Каноническое уравнение прямой
- •V2: де 57 - Фундаментальная система решений линейного однородного дифференциального уравнения
V2: де 2 – Линейные отображения. Транспонирование матриц.
I: {{2.1}}
S:
Матрица
 (
( -
транспонированная по отношению к
-
транспонированная по отношению к матрица), где
матрица), где , имеет вид
, имеет вид
-:

+:

-:

-:

I: {{2.2}}
S:
Матрица
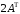 (
( -
транспонированная по отношению к
-
транспонированная по отношению к матрица), где
матрица), где , имеет вид
, имеет вид
-:

-:

-:

+:

I: {{2.3}}
S:
Матрица
 (
( -
транспонированная по отношению к
-
транспонированная по отношению к матрица), где
матрица), где , имеет вид
, имеет вид
+:

-:

-:

-:

I: {{2.4}}
S:
Матрица
 (
( -
транспонированная по отношению к
-
транспонированная по отношению к матрица), где
матрица), где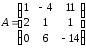 , имеет вид
, имеет вид
-:

-:

+:

-:

I: {{2.5}}
S:
Матрица
 (
(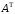 -
транспонированная по отношению к
-
транспонированная по отношению к матрица), где
матрица), где , имеет вид
, имеет вид
+:

-:

-:

-:

I: {{2.6}}
S:
Матрица
 (
( -
транспонированная по отношению к
-
транспонированная по отношению к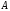 матрица), где
матрица), где , имеет вид
, имеет вид
-:

+:

-:

-:

I: {{2.7}}
S:
Матрица
 (
(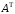 -
транспонированная по отношению к
-
транспонированная по отношению к матрица), где
матрица), где , имеет вид
, имеет вид
-:

-:

+:

-:

I: {{2.8}}
S:
Матрица
 (
( -
транспонированная по отношению к
-
транспонированная по отношению к матрица), где
матрица), где , имеет вид
, имеет вид
-:

-:

-:

+:

I: {{2.9}}
S:
Матрица
 (
( -
транспонированная по отношению к
-
транспонированная по отношению к матрица), где
матрица), где , имеет вид
, имеет вид
+:

-:

-:

-:

I: {{2.10}}
S:
Матрица
 (
( -
транспонированная по отношению к
-
транспонированная по отношению к матрица), где
матрица), где , имеет вид
, имеет вид
-:

+:

-:

-:

I: {{2.11}}
S:
Матрица
 (
(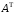 -
транспонированная по отношению к
-
транспонированная по отношению к матрица), где
матрица), где , имеет вид
, имеет вид
-:

-:

+:

-:

I: {{2.12}}
S:
Матрица
 (
( -
транспонированная по отношению к
-
транспонированная по отношению к матрица), где
матрица), где , имеет вид
, имеет вид
-:

-:

-:

+:

I: {{2.13}}
S:
Матрица
 (
( -
транспонированная по отношению к
-
транспонированная по отношению к матрица), где
матрица), где , имеет вид
, имеет вид
+:

-:

-:

-:

I: {{2.14}}
S:
Матрица
 (
( -
транспонированная по отношению к
-
транспонированная по отношению к матрица), где
матрица), где , имеет вид
, имеет вид
-:

+:

-:

-:

I: {{2.15}}
S:
Матрица
 (
( -
транспонированная по отношению к
-
транспонированная по отношению к матрица), где
матрица), где , имеет вид
, имеет вид
-:

-:

+:

-:

I: {{2.16}}
S:
Матрица
 (
( -
транспонированная по отношению к
-
транспонированная по отношению к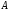 матрица), где
матрица), где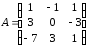 , имеет вид
, имеет вид
-:

-:

-:

+:

I: {{2.17}}
S:
Матрица
 (
( -
транспонированная по отношению к
-
транспонированная по отношению к матрица), где
матрица), где , имеет вид
, имеет вид
+:

-:

-:

-:

I: {{2.18}}
S:
Матрица
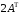 (
( -
транспонированная по отношению к
-
транспонированная по отношению к матрица), где
матрица), где , имеет вид
, имеет вид
-:

+:

-:

-:

I: {{2.19}}
S:
Матрица
 (
( -
транспонированная по отношению к
-
транспонированная по отношению к матрица), где
матрица), где , имеет вид
, имеет вид
-:

-:

+:

-:

I: {{2.20}}
S:
Матрица
 (
( -
транспонированная по отношению к
-
транспонированная по отношению к матрица), где
матрица), где , имеет вид
, имеет вид
-:

-:

-:

+:

I: {{2.21}}
S:
Матрица
 (
(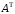 -
транспонированная по отношению к
-
транспонированная по отношению к матрица), где
матрица), где , имеет вид
, имеет вид
+:

-:

-:

-:

I: {{2.22}}
S:
Матрица
 (
( -
транспонированная по отношению к
-
транспонированная по отношению к матрица), где
матрица), где , имеет вид
, имеет вид
-:

+:

-:

-:

I: {{2.23}}
S:
Матрица
 (
( -
транспонированная по отношению к
-
транспонированная по отношению к матрица), где
матрица), где , имеет вид
, имеет вид
-:

-:

+:

-:

I: {{2.24}}
S:
Матрица
 (
( -
транспонированная по отношению к
-
транспонированная по отношению к матрица), где
матрица), где , имеет вид
, имеет вид
-:

-:

-:

+:

I: {{2.25}}
S:
Матрица
 (
( -
транспонированная по отношению к
-
транспонированная по отношению к матрица), где
матрица), где , имеет вид
, имеет вид
+:

-:

-:

-:

V2: де 5 - Линейные отображения. Умножение матриц
I: {{5.1}}
S:
Если
 ,
,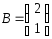 ,
тогда матрица
,
тогда матрица имеет вид
имеет вид
+:

-:
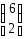
-:

-:

I: {{5.2}}
S:
Если
 ,
, ,
тогда матрица
,
тогда матрица имеет вид
имеет вид
-:

-:

+:

-:

I: {{5.3}}
S:
Даны
две матрицы:
 ,
, .
Элемент первой строки второго столбца
произведения
.
Элемент первой строки второго столбца
произведения равен ###
равен ###
+: 23
I: {{5.4}}
S:
Если
 ,
, ,
тогда матрица
,
тогда матрица имеет вид
имеет вид
-:

-:

+:

-:

I: {{5.5}}
S:
Если
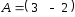 ,
, ,
тогда матрица
,
тогда матрица имеет вид
имеет вид
-:

+:

-:

-:

I: {{5.6}}
S:
Если
 ,
, ,
тогда матрица
,
тогда матрица имеет вид
имеет вид
+:

-:

-:

-:

I: {{5.7}}
S:
Если
 ,
, ,
тогда матрица
,
тогда матрица имеет вид
имеет вид
-:

+:

-:

-:

I: {{5.8}}
S:
Если
 ,
, ,
тогда матрица
,
тогда матрица имеет вид
имеет вид
-:

-:

+:

-:

I: {{5.9}}
S:
Даны
матрицы:
 ,
, .
Сумма элементов матрицы
.
Сумма элементов матрицы ,
расположенных на ее главной диагонали,
равна ###
,
расположенных на ее главной диагонали,
равна ###
+:-2
I: {{5.10}}
S:
Даны
матрицы:
 ,
, .
Сумма элементов матрицы
.
Сумма элементов матрицы ,
расположенных на ее главной диагонали,
равна ###
,
расположенных на ее главной диагонали,
равна ###
+: 5
I: {{5.11}}
S:
Если
 ,
тогда матрица
,
тогда матрица имеет вид
имеет вид
+:

-
:

-
:
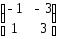
-
:

I: {{5.12}}
S:
Даны:
 ,
, .
Тогда матрица
.
Тогда матрица имеет вид
имеет вид
+:

-:

-:

-:

I: {{5.13}}
S:
Если
 ,
, ,
тогда матрица
,
тогда матрица имеет вид
имеет вид
+:

-:

-:

-:
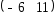
I: {{5.14}}
S:
Если
 ,
, ,
тогда матрица
,
тогда матрица имеет вид
имеет вид
-:
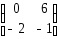
-:

+:

-:

I: {{5.15}}
S:
Даны
две матрицы:
 ,
, .
Элемент первой строки второго столбца
произведения
.
Элемент первой строки второго столбца
произведения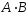 равен ###
равен ###
+: -11
I: {{5.16}}
S:
Если
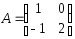 ,
, ,
тогда матрица
,
тогда матрица имеет вид
имеет вид
-:

-:

+:

-:

I: {{5.17}}
S:
Если
 ,
, ,
тогда матрица
,
тогда матрица имеет вид
имеет вид
-:

+:

-:
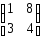
-:

I: {{5.18}}
S:
Если
 ,
, ,
тогда матрица
,
тогда матрица имеет вид
имеет вид
+:
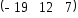
-:

-:
-:

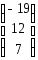
I: {{5.19}}
S:
Если
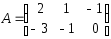 ,
, ,
тогда матрица
,
тогда матрица имеет вид
имеет вид
-:

-:

-:

+:
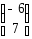
I: {{5.20}}
S:
Если
 ,
, ,
тогда матрица
,
тогда матрица имеет вид
имеет вид
-:

-:

+:

-:

I: {{5.21}}
S:
Даны
матрицы:
 ,
, .
Сумма элементов матрицы
.
Сумма элементов матрицы ,
расположенных на ее главной диагонали,
равна ###
,
расположенных на ее главной диагонали,
равна ###
+: 8
I: {{5.22}}
S:
Даны
матрицы:
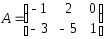 ,
, .
Сумма элементов матрицы
.
Сумма элементов матрицы ,
расположенных на ее главной диагонали,
равна ###
,
расположенных на ее главной диагонали,
равна ###
+: 10
I: {{5.23}}
S:
Если
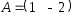 ,
, ,
тогда матрица
,
тогда матрица имеет вид
имеет вид
-:

+
:

-:

-:

I: {{5.24}}
S:
Даны:
 .
Сумма элементов матрицы
.
Сумма элементов матрицы ,
расположенных на ее главной диагонали,
равна ###
,
расположенных на ее главной диагонали,
равна ###
+: -1
I: {{5.25}}
S:
Даны:
 ,
, .
Сумма элементов матрицы
.
Сумма элементов матрицы ,
расположенных на ее главной диагонали,
равна ###
,
расположенных на ее главной диагонали,
равна ###
+: 2
