2 Вариант задания и исходные данные

Вариант задания: 01

Исходные данные приведены в таблице 1.

Таблица 1 Исходные данные

, В	, В	Т, мкс	, мкс
3	3	250	60

Временная диаграмма исходного колебания:

u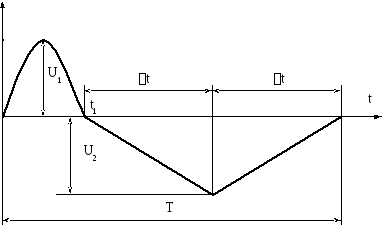(t).

t₂

3 Аналитическая запись колебания u(t)

Сначала выполним спектральный анализ заданного колебания u(t). Для этого, пользуясь графической формой колебания и заданными параметрами, запишем его аналитически. Весь период Т колебания разбиваем на три интервала: [0; t], [t; t₂] и [t₂; T] (точка t₂ =является серединой интервала [t; Т]). Первый интервал представлен синусоидой, второй и третий - линейными функциями. В общем виде аналитическая запись сигнала будет выглядеть так:

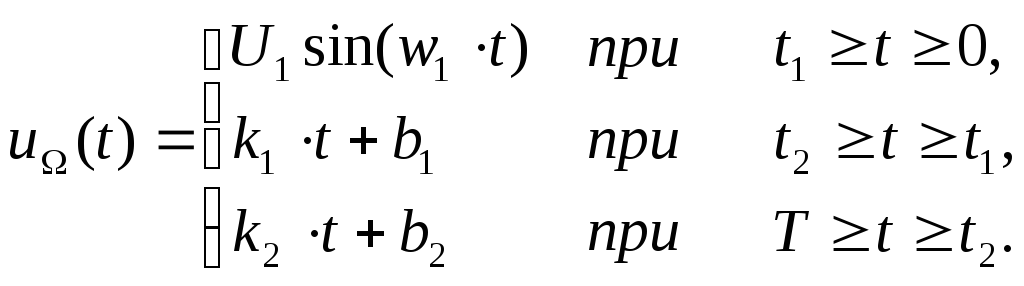(1)

Частота синусоиды (в знаменателе записан период этой синусоиды).

Значения и определяем из системы уравнений:

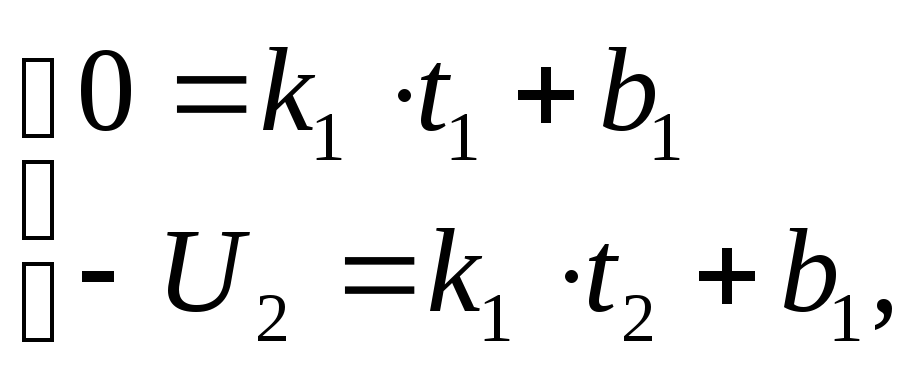
получаемой путем подстановки во второе уравнение системы (1) значений времени и и соответствующих им значений колебанияu(t). Решение указанной системы уравнений дает ,.

Аналогично определяем k₂ и b₂. В третье уравнение системы (1)подставляем значения t₂ и Т и соответствующие им значения колебания u(t) .

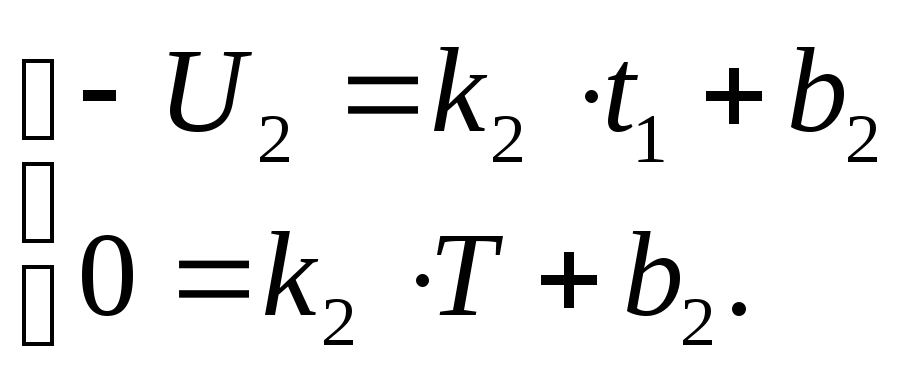
Решив систему, получаем: ,.

В результате изложенного, система уравнений (1) принимает вид:

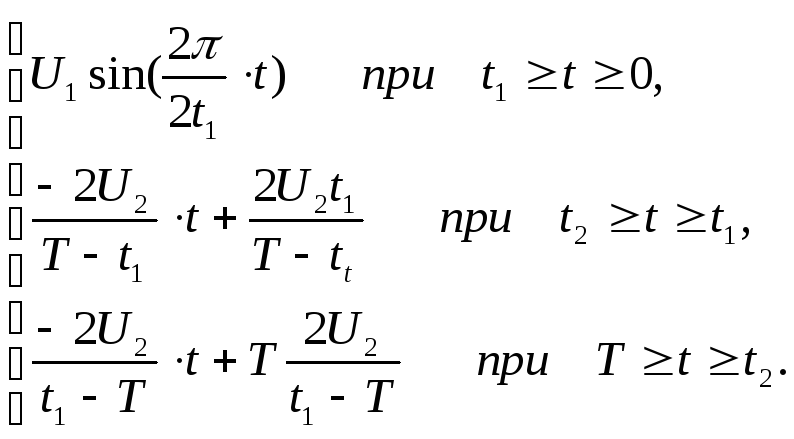
(2)

Для дальнейших расчетов определим:

мкс

В

Периодический сигнал с периодомТ и частотой разлагается в ряд Фурье (для краткости обозначим=):

где - постоянная составляющая сигнала;

- коэффициент ряда Фурье;

- коэффициент ряда Фурье.

Для разложения сигнала в ряд Фурье вычислим значения: первых 5 гармоник.

4 Определение коэффициентов

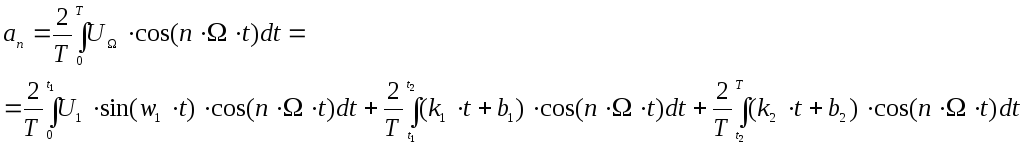
Подсчитаем каждый из интегралов отдельно:

1)

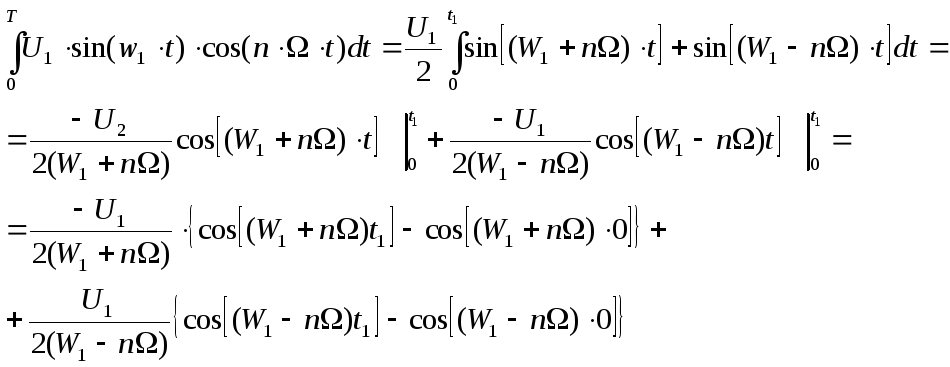
2)

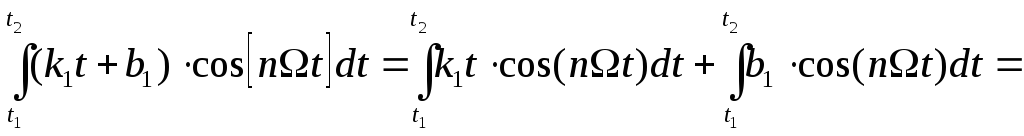
первый интеграл берем по частям:

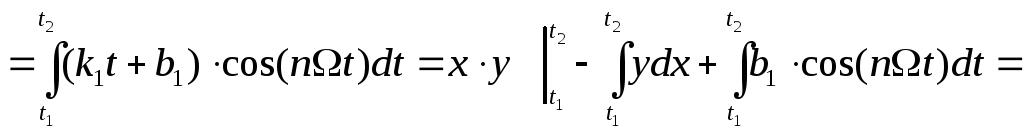
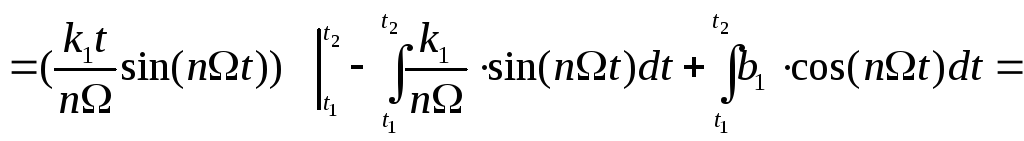
3)

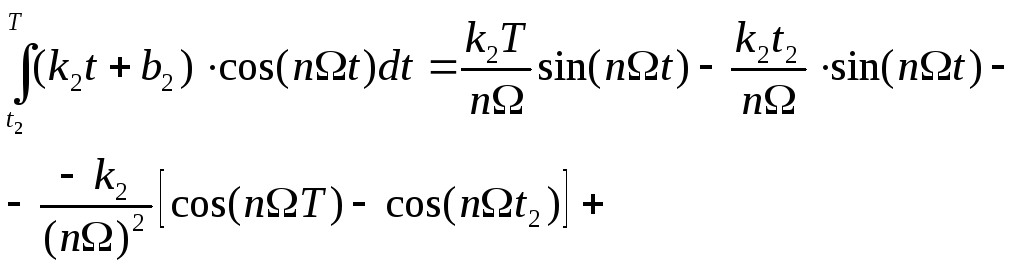
Запишем выражение для как функции порядкового номераn гармоник колебания :

Подставляя ранее вычисленные значения ,заданное значениеи значениянаходим численные значения 5 коэффициентов:

В

В

В

В

В

Полученные результаты заносим в таблицу 2.

5 Определение коэффициентов

Из разложения запишем формулу:

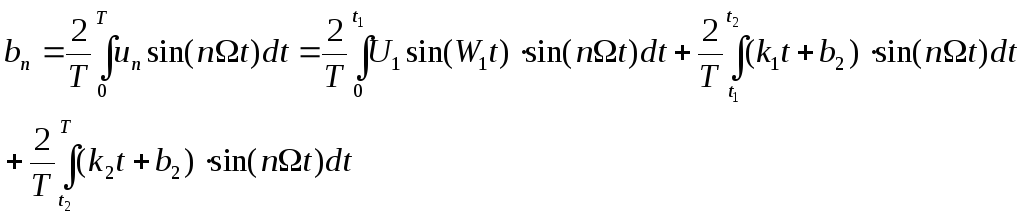
Расчет каждого из интегралов проведем отдельно:

1)

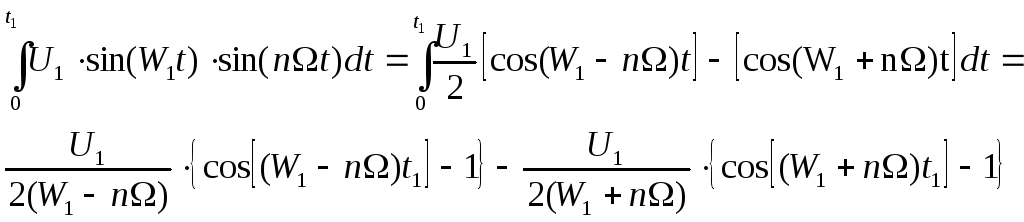
2) ;

; ;;;

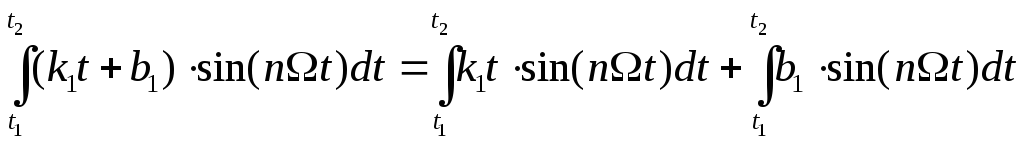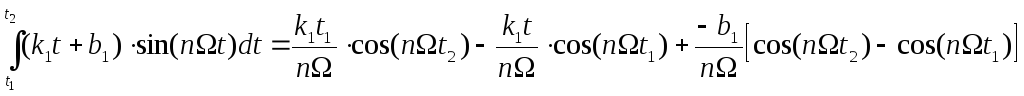
3)

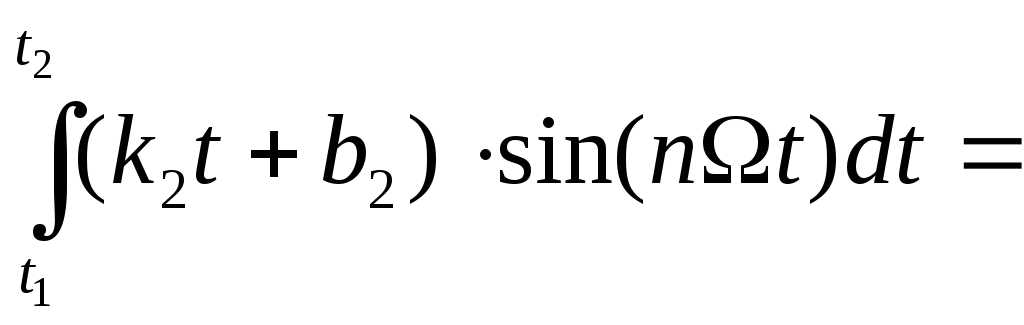
Запишем выражение для как функцию порядкового номераn гармоник колебания :

.

Подставляя ранее вычисленные значения ,заданное значениеи значениянаходим численные значения 5 коэффициентов:

В

В

В

В

В

Полученные результаты заносим в таблицу 2.