
- •Математика
- •Глава 1 подготовлена м. Н. Рассказовой, глава 2 – о. П. Диденко, предисловие, введение, глава 3, алфавитно-предметный указатель – с. Х. Мухаметдиновой.
- •Оглавление
- •Предисловие
- •Введение
- •Глава 1. Элементы линейной алгебры и аналитической геометрии
- •Линейная алгебра
- •Операции над матрицами
- •Свойства операций над матрицами:
- •Определители матриц и их свойства
- •Обратная матрица. Решение матричных уравнений
- •Системы линейных уравнений
- •Построение моделей задач, сводящихся к системам линейных уравнений
- •1.1.6. Применение элементов линейной алгебры в экономике
- •1.1.7. Модель Леонтьева межотраслевого баланса
- •Контрольные задания
- •Векторная алгебра
- •Векторы. Линейные операции над векторами
- •Скалярное, векторное, смешанное произведение векторов
- •Линейные операторы. Собственные векторы и собственные значения
- •Контрольные задания
- •Аналитическая геометрия
- •Прямая на плоскости
- •Окружность. Эллипс. Гипербола. Парабола
- •Прямая и плоскость в пространстве
- •Контрольные задания
- •Глава 2. Математический анализ
- •2.1. Функции одной переменной
- •Контрольные задания
- •2.2. Предел и непрерывность функции
- •Некоторые свойства пределов
- •2.2.1. Замечательные пределы
- •2.2.2. Непрерывность функции в точке
- •Контрольные задания
- •2.3.2. Применение производной в экономике
- •2.3.3. Дифференциал функции
- •Контрольные задания
- •2.4. Приложения производной
- •2.4.1. Исследование функции на монотонность,
- •Экстремумы и выпуклость.
- •Асимптоты графика функции
- •2.4.2. Общая схема исследования функции
- •И построения ее графика
- •Контрольные задания
- •2.5.2. Метод интегрирования по частям
- •2.6.2. Геометрические приложения
- •Определенного интеграла
- •Применение определенного интеграла
- •В экономике
- •Несобственные интегралы
- •Функции нескольких переменных
- •2.7.1. Частные производные, дифференциал,
- •Градиент функции
- •2.7.2. Частные производные 2-го порядка.
- •Исследование функции на экстремум
- •2.7.3. Метод наименьших квадратов
- •Контрольные задания
- •2.8. Дифференциальные уравнения
- •1. Уравнение с разделяющимися переменными
- •2. Однородные уравнения 1-го порядка
- •3. Линейные уравнения 1-го порядка
- •4. Линейные однородные уравнения 2-го порядка
- •С постоянными коэффициентами
- •2.9. Последовательности и ряды
- •2.9.1. Предел последовательности
- •2.9.2. Числовые ряды
- •Достаточный признак расходимости ряда
- •Признаки сходимости рядов с положительными членами:
- •2.9.3. Степенные ряды
- •Контрольные задания
- •3.1.3. Размещения
- •Сочетания
- •Если в формуле (3.5) заменить число k на n − k, то получим:
- •Правило сложения
- •Правило произведения
- •Контрольные вопросы
- •Элементы теории вероятностей
- •3.2.1. Основные понятия теории вероятностей
- •3.2.2. Классификация событий
- •3.2.3. Алгебра событий
- •3.2.4. Статистический подход к понятию вероятности
- •3.2.5. Классический подход к понятию вероятности
- •3.2.6. Решение вероятностных задач
- •С помощью комбинаторики
- •3.2.7. Геометрический подход к понятию вероятности
- •3.2.8. Аксиоматическое определение
- •Понятия вероятности
- •3.2.9. Вероятность суммы несовместных событий
- •3.2.10. Вероятность произведения событий
- •3.2.11. Формула полной вероятности. Формула Байеса
- •3.2.12. Формула Бернулли. Наивероятнейшее число
- •Наступлений события
- •3.2.13. Локальная формула Муавра−Лапласа
- •3.2.14. Интегральная формула Муавра−Лапласа
- •3.2.15. Формула Пуассона
- •Контрольные вопросы
- •3.3. Случайные величины
- •3.3.1. Дискретные случайные величины.
- •Закон распределения дискретной случайной величины
- •3.3.2. Числовые характеристики
- •Дискретных случайных величин
- •Свойства математического ожидания:
- •Свойства дисперсии:
- •3.3.3. Функция распределения вероятностей
- •Случайной величины
- •Основные свойства функции распределения:
- •3.3.4. Непрерывная случайная величина.
- •3.3.5. Числовые характеристики
- •Непрерывных случайных величин
- •3.3.6. Равномерное распределение
- •3.3.7. Нормальное распределение
- •3.3.8. Показательное распределение
- •Контрольные вопросы
- •3.4. Элементы математической статистики
- •Основные задачи математической статистики
- •3.4.1. Основные понятия математической статистики
- •3.4.2. Точечные оценки параметров распределения
- •3.4.3. Интервальные оценки параметров распределения
- •Интервальные оценки параметров нормального распределения:
- •3.4.4. Проверка статистических гипотез
- •Проверка гипотезы о нормальном распределении
- •Генеральной совокупности по критерию Пирсона
- •Алгоритм применения критерия Пирсона
- •Контрольные вопросы
- •Заключение
- •Библиографический список
- •Основная литература
- •Дополнительная литература
- •Приложение 1
- •Приложение 2
- •Приложение 3
- •Приложение 4
- •Приложение 5
- •Приложение 6
- •Глава 2 «Математический анализ»
- •Глава 3 «Теория вероятностей и математическая статистика»
- •3.1. Классическое определение вероятности
- •Теоремы сложения и умножения вероятностей
- •Формулы полной вероятности и Байеса
- •3.4. Схема Бернулли. Теорема Муавра-Лапласа, Пуассона
- •3.5. Случайные величины
- •3.6. Законы распределения
- •3.7. Математическая статистика
- •Алфавитно-предметный указатель
- •Математика
- •644099, Омск, ул. Красногвардейская, 9
3)
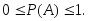
3.2.9. Вероятность суммы несовместных событий
Теорема. Вероятность суммы несовместных событий
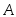 и
и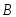 равна сумме вероятностей этих событий:
равна сумме вероятностей этих событий: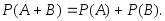 (3.10)
(3.10)Следствие 1. С помощью метода математической индукции формулу (3.10) можно обобщить на любое число попарно несовместных событий:
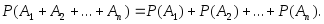 (3.11)
(3.11)Следствие 2. Поскольку противоположные события являются несовместными, а их сумма – достоверным событием, то, используя (3.10), имеем:
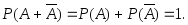 (3.12)
(3.12)Часто при решении задач формулу (3.12) используют в виде:
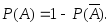 (3.13)
(3.13)Пример 3.29. В опыте с бросанием игральной кости найти вероятности выпадения на верхней грани числа очков более 3 и менее 6.
Обозначим события, связанные с выпадением на верхней грани игральной кости одного очка, через U1, двух очков через U2,…, шести очков через U6.
Пусть событие U – выпадение на верхней грани кости числа очков более 3 и менее 6. Это событие произойдет, если произойдет хотя бы одно из событий U4 или U5, следовательно, его можно представить в виде суммы этих событий:
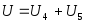 .
Т. к. событияU4
и U5
являются
несовместными, то для нахождения
вероятности их суммы используем формулу
(3.11). Учитывая, что вероятности событий
U1,
U2,…,U6
равны
.
Т. к. событияU4
и U5
являются
несовместными, то для нахождения
вероятности их суммы используем формулу
(3.11). Учитывая, что вероятности событий
U1,
U2,…,U6
равны
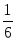 ,
получим:
,
получим: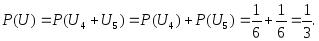
Замечание. Ранее задачи такого типа решали с помощью подсчета числа благоприятствующих исходов. Действительно, событию U благоприятствуют два исхода, а всего шесть элементарных исходов, следовательно, используя классический подход к понятию вероятности, получим:
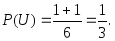
Однако классический поход к понятию вероятности, в отличие от теоремы о вероятности суммы несовместных событий, применим только для равновозможных исходов.
Пример 3.30. Вероятность попадания в цель стрелком равна 0,7. Какова вероятность того, что стрелок не попадет в цель?
Пусть событие
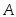 − попадание стрелком в цель, тогда
событие, состоящее в том, что стрелок
не попадет в цель, является противоположным
событием
− попадание стрелком в цель, тогда
событие, состоящее в том, что стрелок
не попадет в цель, является противоположным
событием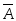 событию
событию ,
т. к. в результате каждого испытания
всегда происходит одно и только одно
из этих событий. Используя формулу
(3.13), получим:
,
т. к. в результате каждого испытания
всегда происходит одно и только одно
из этих событий. Используя формулу
(3.13), получим: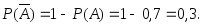
3.2.10. Вероятность произведения событий
Определение. Событие
 называетсязависимым
от события
называетсязависимым
от события
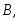 если вероятность события
если вероятность события
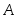 зависит от того, произошло событие
зависит от того, произошло событие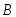 или нет.
или нет.Определение. Вероятность события
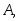 вычисленная при условии, что событие
вычисленная при условии, что событие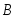 произошло, называетсяусловной
вероятностью
события
произошло, называетсяусловной
вероятностью
события
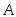 и обозначается
и обозначается
Теорема. Вероятность произведения событий
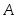 и
и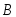 равна произведению вероятности одного
из них на условную вероятность другого,
вычисленную при условии, что первое
имело место:
равна произведению вероятности одного
из них на условную вероятность другого,
вычисленную при условии, что первое
имело место: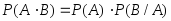 или
или
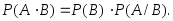 (3.14)
(3.14)Условие независимости события
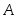 от события
от события
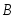 можно записать в виде
можно записать в виде
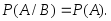 Из этого утверждения следует, что для
независимых событий выполняется
соотношение:
Из этого утверждения следует, что для
независимых событий выполняется
соотношение: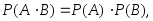 (3.15)
(3.15)т. е. вероятность произведения независимых событий
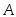 и
и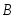 ,
равна произведению их вероятностей.
,
равна произведению их вероятностей.Замечание. Вероятность произведения нескольких событий
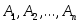 равна произведению вероятностей этих
событий, причем вероятность каждого
следующего по порядку события вычисляется
при условии, что все предыдущие имели
место:
равна произведению вероятностей этих
событий, причем вероятность каждого
следующего по порядку события вычисляется
при условии, что все предыдущие имели
место: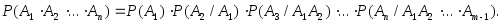
Если события независимые, то имеем:
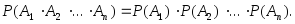
Пример 3.31. В ящике 5 белых и 3 черных шара. Из него наугад последовательно без возвращения вытаскивают два шара. Найти вероятность того, что оба шара белые.
Пусть событие
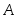 − появление белого шара при первом
вынимании,
− появление белого шара при первом
вынимании,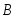 − появление белого шара при втором
вынимании. Учитывая, что
− появление белого шара при втором
вынимании. Учитывая, что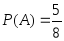 ,
,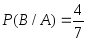 (вероятность появления второго белого
шара при условии, что первый вынутый
шар был белым и его не возвратили в
ящик). Так как события
(вероятность появления второго белого
шара при условии, что первый вынутый
шар был белым и его не возвратили в
ящик). Так как события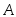 и
и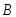 зависимые, то вероятность их произведения
найдем по формуле (3.15):
зависимые, то вероятность их произведения
найдем по формуле (3.15):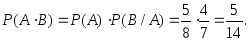
Пример 3.32. Вероятность попадания в цель первым стрелком 0,8; вторым – 0,7. Каждый стрелок выстрелил по мишени. Какова вероятность того, что хотя бы один стрелок попадет в цель? Какова вероятность того, что один стрелок попадет в цель?
Пусть событие
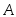 – попадание в цель первым стрелком,
– попадание в цель первым стрелком,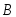 – вторым. Все возможные варианты можно
представить в видетаблицы
3.5,
где «+» обозначает, что событие произошло,
а «−» − не произошло.
– вторым. Все возможные варианты можно
представить в видетаблицы
3.5,
где «+» обозначает, что событие произошло,
а «−» − не произошло.Таблица 3.5
+
+
+
−
−
+
−
−
Пусть событие
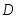 – попадание хотя бы одним стрелком в
цель, Тогда событие
– попадание хотя бы одним стрелком в
цель, Тогда событие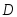 является суммой независимых событий
является суммой независимых событий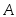 и
и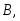 следовательно, применить теорему о
вероятности суммы несовместных событий
в данной ситуации нельзя.
следовательно, применить теорему о
вероятности суммы несовместных событий
в данной ситуации нельзя.Рассмотрим событие
 противоположное событию
противоположное событию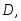 которое произойдет тогда, когда ни
один стрелок не попадет в цель, т. е.
является произведением независимых
событий
которое произойдет тогда, когда ни
один стрелок не попадет в цель, т. е.
является произведением независимых
событий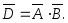 Используя формулы (3.13) и (3.15), получим:
Используя формулы (3.13) и (3.15), получим: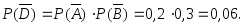
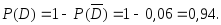
Пусть событие
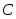 – попадание одним стрелком в цель. Это
событие можно представить следующим
образом:
– попадание одним стрелком в цель. Это
событие можно представить следующим
образом: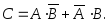
События
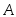 и
и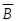 – независимые, события
– независимые, события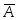 и
и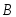 также являются независимыми. События,
являющиеся произведениями событий
также являются независимыми. События,
являющиеся произведениями событий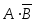 и
и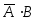 – несовместными. Используя формулы
(3.10) и (3.15) получим:
– несовместными. Используя формулы
(3.10) и (3.15) получим: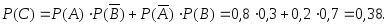
Свойства операций сложения и умножения событий:
1.
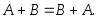
2.
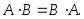
3.
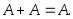
4.
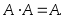
5.
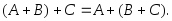
6.
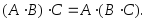
7.
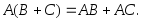
3.2.11. Формула полной вероятности. Формула Байеса
Пусть событие
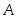 может произойти только вместе с одним
из попарно несовместных событий
(гипотез)
может произойти только вместе с одним
из попарно несовместных событий
(гипотез)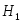 ,
,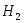 ,…,
,…,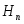 ,
образующих полную группу, т. е.
,
образующих полную группу, т. е.
Вероятность события
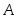 находится по формулеполной
вероятности:
находится по формулеполной
вероятности: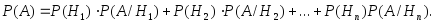 (3.16)
(3.16)Если событие
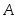 уже произошло, то вероятности гипотез
могут быть переоценены по формулеБайеса:
уже произошло, то вероятности гипотез
могут быть переоценены по формулеБайеса: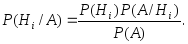 (3.17)
(3.17)Пример 3.33. Имеются две одинаковых урны с шарами. В первой урне 5 белых и 10 черных шаров, во второй − 3 белых и 7 черных шаров. Выбирают наугад одну урну и вытаскивают из нее один шар.
Найти вероятность того, что этот шар белый.
Из наугад выбранной урны вытащили белый шар. Найти вероятность того, что шар вытащили из первой урны.
