Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Кубанский государственный аграрный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Методичка_.pdf

Скачиваний:

Добавлен:

20.03.2016

Размер:

2.03 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 54 5 > Следующая >>>

Линейная алгебра	Типовые расчеты

аналитическая геометрия	методические указания

Задание 6. Решить однородную систему линейных алгебраических уравнений:

1.x1 2x2 x3 0,

4x1 3x2 7x3 0,

5x1 x2 6x3 0.

4.2x1 4x2 3x3 0,

x1 3x2 2x3 0,3x1 x2 x3 0.

7.x1 2x2 3x3 0,2x1 4x2 x3 0,3x1 6x2 4x3 0.

10.7x1 6x2 x3 0,

3x1 3x2 4x3 0,

4x1 3x2 5x3 0.

13.5x1 3x2 2x3 0,

2x1 4x2 3x3 0,

3x1 7x2 5x3 0.

16.2x1 2x2 x3 0,

5x1 4x2 6x3 0,

3x1 2x2 5x3 0.

19.x1 8x2 7x3 0,

3x1 5x2 4x3 0,

4x1 3x2 3x3 0.

2.7x1 5x2 3x3 0,

5x1 4x2 x3 0,2x1 x2 4x3 0.

5.x1 5x2 x3 0,

3x1 2x2 6x3 0,

2x1 3x2 7x3 0.

8.3x1 2x2 x3 0,

2x1 3x2 5x3 0,

5x1 x2 4x3 0.

11.2x1 x2 x3 0,

x1 2x 2 2x3 0,7x1 x2 x3 0.

14.2x1 3x2 4x3 0,

x1 2x2 3x3 0,3x1 x2 x3 0.

17.3x1 4x2 1x3 0,

x1 3x2 5x3 0,4x1 x2 4x3 0.

20.x1 3x2 7x3 0,x1 4x3 0,

3x1 6x2 10x3 0.

3.3x1 2x2 5x3 0,

5x1 4x2 6x3 0,

2x1 2x2 x3 0.

6.3x1 4x2 5x3 0,

2x1 3x2 3x3 0,4x1 11x2 13x3 0.

9.7x1 5x2 3x3 0,

5x1 4x2 x3 0,2x1 x2 4x3 0.

12.9x1 x2 8x 3 0,

2x1 8x2 x3 0,4x1 2x2 3x3 0.

15.x1 5x2 x3 0,2x1 x2 x3 0,3x1 4x2 2x3 0.

18.2x1 x2 4x3 0,

4x1 9x2 2x3 0,

x1 5x2 3x3 0.

21.x1 x2 x3 0,

2x1 3x2 2x3 0,

x1 x2 x3 0.

- 30 -

Линейная алгебра

Типовые расчеты

аналитическая геометрия

методические указания

22.

4x 2 x3 0,

23.

x2 x3 0,

24.

x2 2x3 0,

3x1

x2 x3 0,

4x1

x1 3x2 2x3 0,

4x1 5x2 3x3 0,

7x2

3x3 0.

3x2 x3 0.

x1 5x 2 2x3 0.

5x1

2x1

25.

3x1

x2 x3 0,

26.

2x1

x3 0,

27.

x1 4x2 7x3 0,

3x2 4x3 0,

7x 2

6x3 0,

2x2 3x3 0,

2x1

2x2 3x3 0.

4x3 0.

3x2 5x3 0.

5x1

3x1 x2

28.

x1 2x2 x3 0,

29.

x3 0,

30.

3x1

2x2 x3 0,

3x2 5x3 0,

5x3 0,

3x1

2x1

x1 x2 2x3 0,

x2 6x3 0.

2x2

3x3 0.

4x2 3x3 0.

4x1

2x1

Решение типового примера.

Пусть требуется исследовать на совместность и решить следующую систему уравнений:

2x1 x2 4x3 0,3x1 4x2 x3 0,

x1 3x2 3x3 0.

Данная система уравнений однородная, следовательно, заведо-

мо совместная, поскольку имеет нулевое решение x1 x2 x3 0 ,

значит, осталось выяснить определенная она или неопределенная. Для этого вычислим ранг матрицы системы, и сравним с числом неизвестных переменных.

- 31 -

Линейная алгебра	Типовые расчеты

аналитическая геометрия	методические указания

Полученная ступенчатая матрица имеет две линейно независимые строки, значит r A 2. Так как ранг меньше числа неизвестных переменных r 2 n 3 , то делаем вывод о неопределенности данной однородной системы линейных уравнений.

Поскольку r 2 , две неизвестные переменные основные, одна вспомогательная.

Проверим, являются ли основными неизвестные x1, x2 ?

1	3	1 0	x	, x	2	основные неизвестные, а x	3	вспо-
0	1		1		2		3
0	1

могательная переменная.

По матрице ступенчатого вида составим систему уравнений и разрешим ее относительно основных переменных.


x 3x 3x			0,	x 3 2x		3x 0,	x 3x ,
1	2	3		1	3	3	1	3
x2 2x3 0.				x2 2x3.			x2 2x3.

Таким образом, общее решение исходной однородной системы имеет вид:

3x3 ; 2x3 ; x3 ,

или

3t; 2t; t ,

где t произвольное действительное число.

Ответ. 3t; 2t; t .

- 32 -

Линейная алгебра	Типовые расчеты

аналитическая геометрия	методические указания

Тема 2. Элементы векторного анализа и аналитической геометрии

Задание 7. Даны координаты точек A, B и C в системе x O y . Найти:

а) координаты векторов AB , AC , их разложение по ортам i , j и их модули;

б) угол между векторами AB и AC ;

в) направляющие косинусы векторов AB и AC ; г) проекцию вектора AB на вектор AC .

1.									8;		3					4; 12				.	2.						5; 7										2	.
	A	8;10			, B				8;		3	, C				4; 12				.		A 11; 20			, B		5; 7					, C			7;		2	.
3.		2;																	9		4.
	A	2;			4		,		B 10; 5				,	C				8;	9	.		A	2; 5	, B 14; 4							, C 18;18							.
5.															9;				3		6.		5; 0														5
	A 1; 2			, B				11;11 , C							9;				3	.		A	5; 0		, B			7; 9		, C				5;			5	.
7.			7; 2																3	.	8.		6; 2													4; 7			.
	A		7; 2			, B				5;11 , C							3;		3	.		A	6; 2			, B			6; 7				, C			4; 7			.

9.A 8; 4 , B 4; 5 , C 2; 9 . 10. A 0; 1 , B 12; 8 , C 10; 6 .

11. A 6;1 , B 6;10 , C 4; 4 . 12. . A 2; 3 , B 4; 5 , C 6; 7

13.	A 3; 0 , B				9; 9 , C							7; 5 .						14.	A	3; 3 , B 9; 6 , C 7; 8 .
15.						5; 10												16.					8; 8
	A	7; 1 , B				5; 10						, C			3; 4		.		A	4;1 , B			8; 8				, C		6; 6			.
17.	A 1; 2 , B 13; 7 , C 11; 7															.		18.	A	2; 2 , B 10; 7							, C 8; 7 .
19.	A 8; 4 , B 4; 5 , C 2; 9															.		20.	A	0; 3 , B 12; 6 , C 10; 8 .
21.	A 7; 1 , B 5; 8 , C 3; 6															.		22.	A	7; 5 , B 5; 4 , C 3;10											.
23.			5; 2				7;										.	24.		9; 2										7			.
	A		5; 2	, B			7;		7		, C			5; 7			.		A	9; 2		, B		3; 7		, C 1;				7			.
25.	A		0; 3 , B 12; 6 , C 10; 8 .															26.	A	2;1 , B 10;10 , C 8; 4											.
27.															6			28.		1; 0										5
	A		4; 1 , B					8; 8		, C			6;		6		.		A	1; 0	, B 11; 9				, C			9;		5		.
29.	A 3; 3 , B 9; 6 , C 7; 8 .																	30.	A 3; 0 , B 9; 9 , C 7; 5 .
																- 33 -

Линейная алгебра	Типовые расчеты

аналитическая геометрия	методические указания

Решение типового примера.

Пусть даны координаты точек A 4; 3 ; B 16; 6 ; C 20;16 .

а) Найти координаты векторов AB , AC , их разложение по ортам i , j и их модули.

Известно, что произвольный вектор a , отнесенный к прямоугольной системе координат xOy , может быть представлен в виде:

a a x i a y j .

Данное представление вектора a называется его разложени-

ем по ортам координатных осей i , j .

Если вектор задан начальной M 1 x1; y 1 и конечной точкой

M 2 x 2 ; y 2 , то данное разложение может быть представлено в виде:

M 1 M 2 x 2 x1 i y 2 y 1 j .

В нашем случае имеем:
AB 16 4 i 6 3 j	12i 9 j	AB 12; 9 ,
AC 20 4 i 16 3 j	16i 13 j	AC 16;13 .

Зная координаты вектора a a x ; a y можно найти модуль век-

тора по формуле:

a 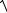a 2x a 2y .

В нашем случае имеем:

	12 2 9 2
AB	12 2 9 2		144 81		225 15 ( лин. ед.),

AC	16 2 132	256 169		425 5 17 ( лин. ед.).
			- 34 -

Линейная алгебра			Типовые расчеты

аналитическая геометрия			методические указания
б) Найти угол между векторами AB и AC .
Воспользуемся формулой
cos a b	a b		,

	a	b

где a b скалярное произведение векторов, которое вычисляется по формуле:

ab a x b x a y b y .

Внашем случае имеем:

cos AB AC	AB AC				12 16 9 13
	AB AC				12 16 9 13	75	1			17	.
											.
	AB		AC		15 5 17	75 17	17			17


			17					17
то есть cos AB AC			17	0, 242 AB AC arccos				17	76 o .
то есть cos AB AC		17		0, 242 AB AC arccos			17		76 o .
		17					17

в) Найти направляющие косинусы векторов AB и AC . Направление произвольного вектора a определяется углами

, образованными им с координатными осями. Косинусы этих углов называются направляющими косинусами и определяются по формулам:

		cos		a x		,		cos					a y	.
				a									a


В нашем случае имеем:
В нашем случае имеем:
1.	AB 12; 9 :	cos	a x		12				4		;	cos			a y		9		3	.

			a		15				5							a	15		5



2.	AC 16; 13 :	cos	a x		16					;		cos			a y		13	.

			a		5		17									a	5 17
			a		5		17									a	5 17
					- 35 -
					- 35 -

Линейная алгебра	Типовые расчеты

аналитическая геометрия	методические указания

г) Найти проекцию вектора AB на вектор AC .
Воспользуемся формулой
					Пр			a	a b			.
							b				b



В нашем случае имеем:
В нашем случае имеем:
Пр		AB	AB AC			12 16				9 13				75		15	.
Пр	AC	AB															.
	AC			AC				5 17					5	17	17
				AC				5 17					5	17	17

Задание 8. Даны координаты вершин треугольника ABC . Найти: а) длины сторон треугольника;

б) уравнения сторон треугольника, указать их угловые коэффициенты и координаты направляющих и нормальных векторов соответственно; в) угол C треугольника ABC ;

г) уравнение высоты AL и ее длину; д) уравнение медианы BK ;

е) уравнение прямой, проходящей через точку L , параллельно стороне AB ;

ж) координаты точки T , расположенной симметрично точке C относительно высоты AL ;

з) сделать рисунок.

5; 7

7; 2

4;12

12; 1

, C

A 11; 20

, C

A 13;10 ,

B 3; 5 ,

C 15; 4 .

A 17; 5 ,

B 7; 0 ,

C 19; 9 .

A 3;15 ,

B 7;10 ,

C 5;1 .

A 15; 8 ,

B 5; 3 ,

C 17; 6 .

A 7;15 ,

B 3;10 ,

C 9;1 .

A 15;19 ,

B 1; 6 , C 11; 3 .

A 18;14 ,

B 2;1 ,

C 14; 8 .

10.

A 15;14 ,

B 1;1 , C 11; 8 .

11.

A 2;13 ,

B 14; 0 ,

C 2; 9 .

12.

A 9; 8 ,

B 7; 5 , C 5; 14 .

- 36 -

	Линейная алгебра					Типовые расчеты

аналитическая геометрия						методические указания
13.	A 5;14 ,	B 5; 9 ,	C 7; 0 .	14.	A 10; 8 ,	B 0; 3 ,	C 12; 6 .
15.	A 3; 9 , B 7; 4 , C 5; 5 .			16.	A 14; 6 ,	B 4;1 ,	C 16; 8 .
17.	A 7;15 ,	B 3; 0 ,	C 9;1 .	18.	A 6;17 ,	B 4;12 , C 8; 3 .
19.	A 0;10 ,	B 10; 5 , C 2; 4 .		20.	A 13;11 ,	B 3; 6 ,		C 15; 3 .
21.	A 4;13 ,	B 6; 8 ,	C 6; 1 .	22.	A 8;12 ,	B 2; 7 ,		C 10; 2 .
23.	A 15;17 ,	B 1; 4 ,	C 11; 5 .	24.	A 18;18 ,	B 2; 5 ,		C 14; 4 .
25.	A 12; 23 , B 4;10 , C 8;1 .			26.	A 17;13 ,	B 1; 0 ,		C 13; 9 .
27.	A 7;19 ,	B 9; 6 ,	C 3; 3 .	28.	A 16;15 ,	B 0; 2 ,		C 12; 7 .
29.	A 6; 22 ,	B 10; 9 , C 2; 0 .		30.	A 8;10 ,	B 8; 3 , C 4; 12 .

Решение типового примера.

Пусть даны координаты вершин треугольника:

A 4; 3 ; B 16; 6 ; C 20;16 .


а) Найти длины сторон треугольника ABC .
		Используем формулу, определяющую расстояние											d между
точками M 1 x1; y1 и M 2 x2 ;						y 2 :

				d	x2 x1 2 y 2				y1 2				8.1
		Тогда, по формуле (8.1) получим:

			16 4 2 6 3 2					12 2 9 2					лин. ед. ;
	AB		16 4 2 6 3 2					12 2 9 2			225 15		лин. ед. ;

			20 16 2	16 6 2									лин. ед. ;

	BС							4 2 222		500 10		5

			20 4 2	16 3 2									лин. ед. .

	AС						16 2 132			425 5		17

- 37 -

Линейная алгебра	Типовые расчеты

аналитическая геометрия	методические указания

б) Найти уравнения сторон треугольника, указать их угловые коэффициенты и координаты направляющих и нормальных векторов соответственно.

Используем формулу уравнения прямой, проходящей через

две точки M 1 x1; y1 и M 2 x2 ; y 2		:
	x x1		y y1	8.2
	x2 x1		y 2 y1

Подставляя в формулу (8.2) координаты соответствующих вершин треугольника ABC , определим искомые уравнения сторон.

AB :

x 4

y 3

;

x 4

y 3

;

x 4

y 3

;

16 4

6 3

или

3 x 4 4 y 3 ; 3x 12 4 y 12;

3x 4 y 24 0

Получили общее уравнение прямой АВ. Разрешим это уравнение относительно переменной y , тогда коэффициент перед переменной x является угловым коэффициентом прямой АВ:

3x 4 y 24 0имеют следующие4 y координаты3x :		24;	y		3 x 6		k AB 3 .
	и направляющий		p	вектора этой прямой,
	n A; B	и p B; A			4	8.3		4
	n A; B	и p B; A				8.3
Если прямая задана своим общим уравнением Ax By C 0,
	Значит, для прямой АВ:
то нормальный n	n AB 3; 4 ,	p AB 4; 3 .
то нормальный n

- 38 -

Линейная алгебра	Типовые расчеты

аналитическая геометрия	методические указания

Аналогично, используя формулы (8.2) и (8.3) определим уравнения сторон ВС и АС и координаты их нормальных и направляющих векторов соответственно.

BC :

x 16

y 6

;

x 16

y 6

;

x 16

y 6

;

20 16

16 6

11 x 16 2 y 6 ;

11x 176 2 y 12;

11x 2 y 188 0 BC

11x 2 y 188 0

x 94

Координаты нормальных и направляющих векторов:

n BC 11; 2 и n BC 2;11 .

AC :

x 4

y 3

;

x 4

y 3

; 13 x 4 16 y 3 ;

16 3

20 4

13x 52 16y 48;

13x 16y 4 0

13x 16 y 4 0 y

Координаты нормальных и направляющих векторов:

n AC 13; 16

и n AC 16;13 .

в) Определить величину угла B треугольника ABC .

Если две прямые l1 и l 2

заданы уравнениями с угловыми ко-

эффициентами: l1 : y k1x b1

и l2 :

y k 2 x b2 , то угол между ни-

ми можно найти по формуле:

k 2 k1

8.4

k1 k

В нашем случае: k

, значит:

- 39 -

Линейная алгебра									Типовые расчеты

аналитическая геометрия									методические указания
	11			3		25		25



	2

tg				4		4		4	2 .
tg		11			3			25	2 .
	1	11			3	1	33	25



			2		4		8	8
			2		4		8	8

Таким образом, tg 2 arctg2 64 o . г) Найти уравнение высоты CD и ее длину.

Поскольку CD является высотой треугольника АВС, значит CD AB . Используем условие перпендикулярности двух прямых:

прямые перпендикулярны, если их угловые коэффициенты обратно пропорциональны и взяты с противоположными знаками, т.е.

l		l		k				1		.
l	1	l	2	k	l					.
	1		2		l	1		k l
						1
									2
В нашем случае: CD AB k									1		1			4	.
В нашем случае: CD AB k							CD					3			.
							CD		k AB				3
													3
											4
											4

Далее, используем уравнение прямой, проходящей через дан-

ную точку M 0 x0 ; y0 в заданном направлении (оно определяется угловым коэффициентом):

y y0 k x x0

8.5

В нашем случае известна точка C 20;16 точка, через кото-

рую проходит высота CD, и угловой коэффициент этой прямой

k			4	. Тогда получим:
k	CD			. Тогда получим:
	CD	3
		3
		y 16			4	x 20 ;	3y 48 4x 80;	4x 3y 32 0	CD
		y 16			3	x 20 ;	3y 48 4x 80;	4x 3y 32 0	CD

Для определения длины высоты CD, используем формулу (6.1), но сначала найдем координаты точки D. Поскольку точка D является

- 40 -

Линейная алгебра	Типовые расчеты

аналитическая геометрия	методические указания

пересечением прямых CD и AB, то для определения еѐ координат необходимо решить совместно уравнения этих прямых, т.е.

AB 3x 4 y 24 0, ( 4)			3x 4 y 24 0,	x 8,
CD		0. 3
CD	4x 3y 32	0. 3	25y 0.	y 0.

Значит, точка D имеет следующие координаты: D 8; 0 .

Теперь по формуле (8.1) получим:

	20 8 2 16 0 2			20 лин. ед. .
		12 2 162
CD			400

д) Найти уравнение медианы BK .

Так как BK является медианой, то точка K середина отрезка AC. Определим координаты середины отрезка AC по формуле:

			x A xC						20 4
x K				,			x K			,	x		12,
x K		2		,			x K	2		,	x	K	12,
		2						2				K		K 12; 9,5 .
			y A yC					16 3					9,5.	K 12; 9,5 .
y			y A yC			y K		16 3			y K		9,5.
					.					.


	K	2						2
		2						2

Далее, использую формулу (8.2), найдем уравнение медианы BK:

x 16

y 6

;

x 16

y 6

; 31 x 16 8

y 6 ;

12 16

9,5 6

31x 496 8y 48;

31x 8y 448 0

е) Найти уравнение прямой,

проходящей через точку D , парал-

лельно стороне AС.

Пусть l искомая прямая. Тогда, по условию она параллельна прямой AС. Используем условие параллельности двух прямых:

две прямые параллельны, если они имеют равные угловые коэффициенты, т. е.

l1 || l2 kl1 kl 2 .

- 41 -

Линейная алгебра	Типовые расчеты

аналитическая геометрия	методические указания

В нашем случае: k l k AB 1613 .

Также, по условию, известно, что прямая l , проходит через точку D. Тогда используя формулу (8.5), определим уравнение искомой прямой:

D 8; 0

8.5

x 8 ;

y 0

16 y 13x 104;

13x 16 y 104 0

ж) Найти координаты точки T , расположенной симметрично точке B относительно высоты CD .

По условию, точка T симметрична точке B, относительно высоты CD, значит, точка T лежит на прямой AB и длины отрезков BD и DT равны между собой. То есть, точка D является серединой отрезка BT:

	x	B	x	T
x D		B		T	,
x D			2		,
			2
	y B		yT
	y B		yT
y D						.
y D			2			.
			2

Отсюда, найдем искомые координаты точки T.

2 x

2 8 16,

T 0; 6

2 y D y B .

2 0 6.

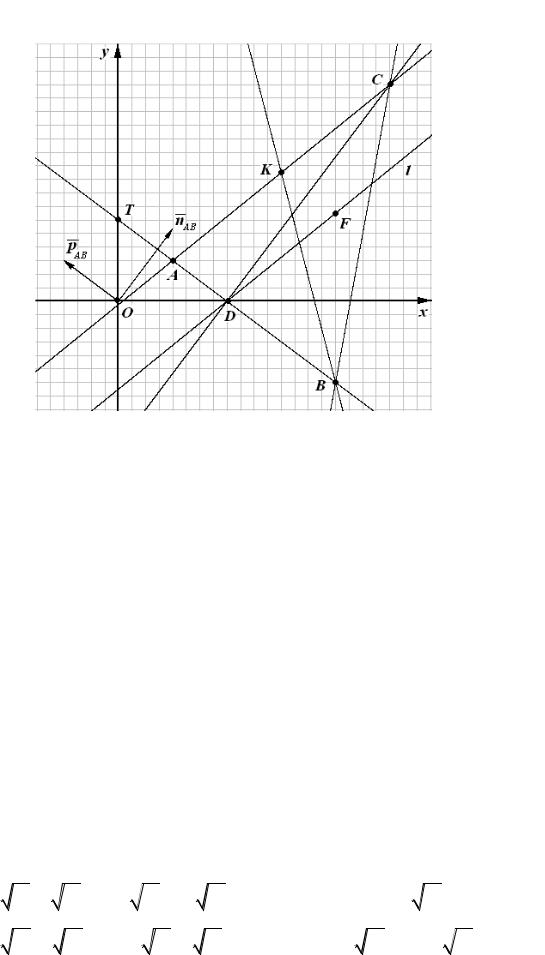
з) Чертеж (рис.1)

Замечание. Для построения прямой l (пункт е) необходимо выбрать дополнительную точку. Например, x 16 y 6,5 F 16; 6,5 .

- 42 -

Линейная алгебра	Типовые расчеты

аналитическая геометрия	методические указания

Рисунок — 1

Задание 9. Даны точки A x1; y1 и B x2 ; y 2 . Требуется:

№№ 1 – 15.

а) составить каноническое уравнение эллипса, проходящего через точки A и B , найти его полуоси, фокусы, эксцентриситет, уравнение директрис. Сделать чертеж.

б) составить уравнение гиперболы, фокусы и вершины которой находятся соответственно в вершинах и фокусах найденного в п. а) эллипса. Найти еѐ асимптоты, директрисы, эксцентриситет. Сделать чертеж.

в) составить уравнение параболы с вершиной в начале координат, симметричной относительно оси Ox и проходящей через точку A x1; y1 . Найти еѐ фокус, уравнение директрисы. Сделать чертеж.

	A 2						; B				; 2					.		A 8; 4 ; B 4				; 2 .
1.		3	; 2		6				6					7			2.				7
	A 4							; B 4							.			A 6; 2		; B 3				; 6 .
3.		2		; 2		6				5		; 2	3				4.		6				2
													- 43 -


	Линейная алгебра																																			Типовые расчеты

аналитическая геометрия																																		методические указания
	A											; B 4							; 4 .								A 2					;					; B 1; 2 .
5.	A	6	; 2						11			; B 4					6		; 4 .							6.	A 2		2			;			6		; B 1; 2 .
	A 4; 2							; B 4																.			A			;						; B 3;						.
7.	A 4; 2				7			; B 4						6		; 2					2			.		8.	A	3		;				6		; B 3;				2		.
	A 3;						;				B 3												.				A 4; 2 ; B 2;												.
9.	A 3;		42				;				B 3		6 ; 2								3		.			10.	A 4; 2 ; B 2;											7	.
	A 2;									;		B 2													.		A				; 2 ; B 3;												.
11.	A 2;					7				;		B 2			2 ;							6			.	12.	A	6			; 2 ; B 3;										2		.
	A			; 2 ; B																.							A 2						; 4 ; B 6; 2											.
13.	A	6		; 2 ; B									3 ;					6		.						14.	A 2		6				; 4 ; B 6; 2									2		.

15. A 2; 4 ; B 7 ; 2 .

№№ 16 – 30.

а) составить каноническое уравнение гиперболы, проходящей через точки A и B , если фокусы гиперболы расположены на оси абсцисс. Найти еѐ полуоси, фокусы, эксцентриситет, уравнения асимптот и директрис. Сделать чертеж.

б) составить уравнение эллипса фокусы и вершины большей оси которого находятся соответственно в вершинах и фокусах найденной в п. а) гиперболы. Найти его оси и уравнения директрис. Сделать чертеж.

в) составить уравнение параболы с вершиной в начале координат, симметричной относительно оси Oy и проходящей через точку

A x1; y1 , найти ее фокус, уравнение директрисы. Сделать чертеж.


	A				; 2 ; B 2														; 2						.								A 4; 6 ; B 6; 4						.
1.	A	6			; 2 ; B 2											2			; 2				3		.							2.	A 4; 6 ; B 6; 4				6		.
	A 2											; B 2																		.			A 8;12 ; B 6; 2									.
3.	A 2		7			; 6			2			; B 2						5 ; 4									3			.		4.	A 8;12 ; B 6; 2						15			.
5. A 8;12 ; B 4															; 2									.									A 3; 4 ; B 5; 4							.
5. A 8;12 ; B 4														3	; 2							6		.								6.	A 3; 4 ; B 5; 4					5		.
	A 6; 4									; B 2																			.				A 3; 4 ; B			; 2 .
7.	A 6; 4							6		; B 2							3 ; 2									6			.			8.	A 3; 4 ; B	6		; 2 .
	A 4												; B 4																		.		A 8; 6 ; B 8					; 2					.
9.	A 4			2			; 4				3		; B 4							3	; 2							6			.	10.	A 8; 6 ; B 8		2			; 2			15		.
																									- 44 -

Линейная алгебра

Типовые расчеты

аналитическая геометрия

методические указания

A 3

; 2

;

B 8; 9

A 4; 3 ; B 8; 9 .

11.

12.

A 8; 9 ;

B 3

A 8; 6 ; B 10; 3

13.

2 ; 2 3

14.

A 10; 3

; B 4

; 6

15.

Решение типового примера.

Пусть даны точки A 6; 2

;

B 2

; 2

. Требуется:

а) Составить каноническое уравнение эллипса, проходящего через точки A и B, найти его полуоси, фокусы, эксцентриситет, уравнение директрис. Сделать чертеж.

Каноническое уравнение эллипса имеет вид:

x 2	y 2	1,	9.1
a 2	b 2

где а и b большая и малая полуоси эллипса.

По условию, эллипс проходит точки A и B, значит, их координаты удовлетворяют уравнению эллипса.

С одной стороны координаты точки A, удовлетворяют уравнению эллипса, т. е.

		2		2
6	2				2		36	8
	2
						1;			1.
a 2			b 2			1;	a 2	b 2	1.
a 2			b 2				a 2	b 2

С другой стороны координаты точки B, удовлетворяют уравнению эллипса, т.е.

2		2	2		2
	3			6		1;	12	24	1.
a 2			b 2				a 2	b 2

Решим совместно полученные два уравнения, откуда определим значения a и b.

- 45 -

Линейная алгебра																																									Типовые расчеты

аналитическая геометрия																																							методические указания
		36					8																				64
													1,																				2,									b 2		32,
		a	2					b		2			1,																b		2		2,									b 2		32,
		a						b																					b
		12					24																				12							24						12					24	1.
													1.																									1.
																	( 3 )																									a	2		32

		a		2				b			2																	a		2					b		2
				2							2																			2							2

	b 2				32,												2								a		4
	b 2				32,												2															3 ,
																				32,												3 ,
														b						32,
	12						1		.							a	2			48.						b 4
	12						1
																																2 .
				2
		a		2			4


Тогда уравнение эллипса примет вид:
											x 2									y 2					1,			или									x 2		y 2		1.
						4						3			2			4				2		2	1,			или						48					32		1.
															2									2

	Фокусы эллипса имеют координаты: F1 c; 0 и F2 c; 0 , где

c	a 2 b 2 .

																			4				2		4						2
В нашем случае:													c						4		3		2		4				2		2							48 32				16			4 .
	Значит, фокусы имеют координаты: F1 4; 0																																							и F2 4; 0 .
	Эксцентриситет эллипса равен:																																	c		.
	Эксцентриситет эллипса равен:																																			.
																																		a

В нашем случае:	4	1	3	.
			3

4	3	3

Уравнения директрис эллипса имеют вид:

:x a ,

:x a .

В нашем случае: d		: x	4 3	12, и d		:	x 12.
	1				2
		1

Вершины эллипса имеют координаты:

- 46 -

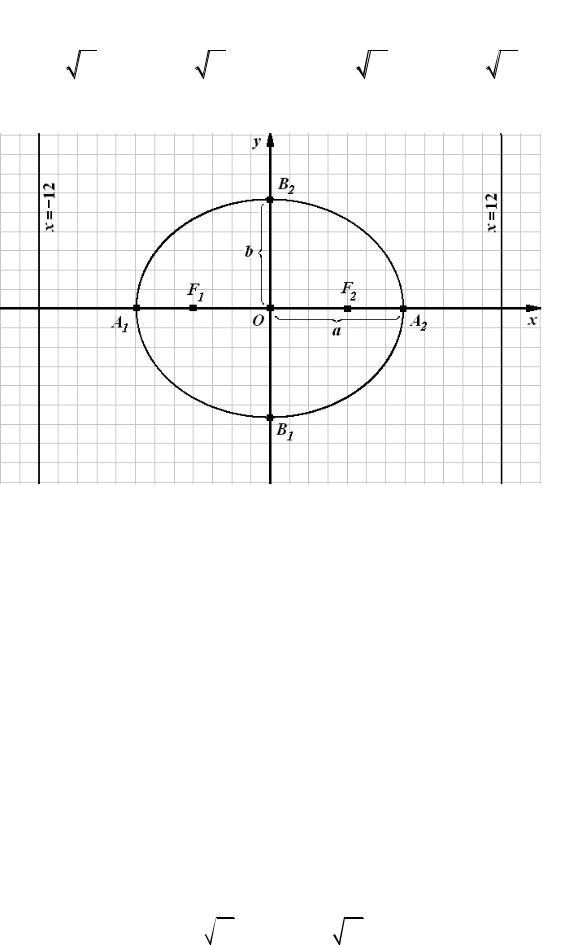
Линейная алгебра									Типовые расчеты

аналитическая геометрия									методические указания
A1 4		; 0 ;	A2 4		; 0 ;	B1 0; 4		;	B2 0; 4		.
	3			3			2			2

Чертеж (рис. 2).

Рисунок — 2

б) Составить уравнение гиперболы, фокусы и вершины которой находятся соответственно в вершинах и фокусах найденного в п. а) эллипса. Найти еѐ асимптоты, директрисы, эксцентриситет. Сделать чертеж.

По условию, вершины гиперболы совпадают с фокусами, найденного в пункте а) эллипса, т. е. точки

F1 4; 0 и F2 4; 0 ,

являются вершинами гиперболы. Значит, большая полуось гиперболы равна 4, a 4 .

Далее по условию, фокусы гиперболы совпадают с вершинами эллипса, лежащими на оси Ox , т.е. с точками

A1 4 3 ; 0 ; A2 4 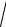3 ; 0 .

Соответственно координаты фокусов гиперболы будут:

- 47 -

Линейная алгебра	Типовые расчеты

аналитическая геометрия	методические указания

F1 4		; 0 ;			F2 4				; 0 ,
F1 4	3	; 0 ;			F2 4		3		; 0 ,
Отсюда получаем, что c 4
Отсюда получаем, что c 4				3 .
Т.к. c 2 a 2 b 2 имеем, что
								4			.
			4			2 4 2
b a 2 c 2
b a 2 c 2					3					2

Соответственно уравнение гиперболы примет вид:

	x 2			y 2			1, или	x 2			y 2	1.
	4	2	4		2	2	1, или					1.
	4		4		2			16	32


Эксцентриситет гиперболы также равен:										c	.
Эксцентриситет гиперболы также равен:											.
										a

В нашем случае:			4	3
			4	3			3 .
			4				3 .
			4

d1 :

Уравнения директрис гиперболы также имеют вид:

d 2 :

В нашем случае:

d		: x	4		4	3	, и d		: x	4 3	.
	1							2

			3	3					3

Уравнения асимптот гиперболы имеют вид:

l		: y	b	x	и	l		: y	b	x.
l	1	: y	a	x	и	l	2	: y	a	x.
	1						2

В нашем случае:

: y

x 2 x и

: y 2 x.

Чертеж (рис. 3).

x a , x a .

- 48 -

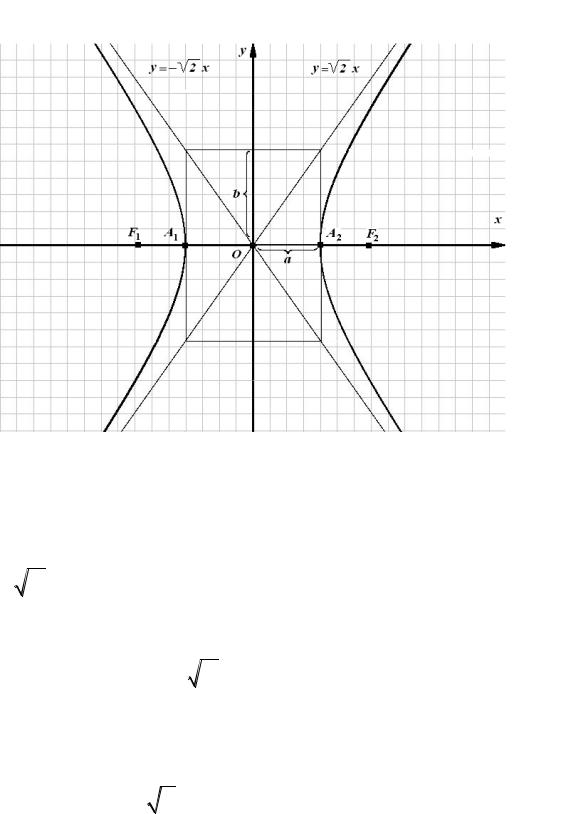
Линейная алгебра	Типовые расчеты

аналитическая геометрия	методические указания

				Рисунок — 3
в) Составить уравнение параболы с вершиной в начале координат,
симметричной относительно					оси Ox и проходящей через точку
A 6; 2		. Найти еѐ фокус, уравнение директрисы. Сделать чертеж.
	2
Поскольку ветви параболы симметричны оси Ox , и она про-
ходит через точку A 6; 2						, т. е. ветви направлены влево от на-
					2
чала координат, то еѐ уравнение имеет вид: y 2 2 px .									Та

Так как координаты точки A, удовлетворяют уравнению пара-
болы, то получим: 2				2	2 p 6; 8 12 p;		p	2
			2

							3

- 49 -

Линейная алгебра							Типовые расчеты

аналитическая геометрия					методические указания
						p
Фокус данной параболы имеет координаты:					F			; 0 . В нашем
Фокус данной параболы имеет координаты:					F			; 0 . В нашем
						2
1					x			p
случае: F	; 0 . Уравнение директрисы			d :					. Соответст-
случае: F	; 0 . Уравнение директрисы			d :					. Соответст-
3							2
венно, в нашем случае: x		1	.
венно, в нашем случае: x		3	.
		3

Чертеж (рис. 4)

Рисунок — 4

Задание 10. Даны координаты вершин пирамиды ABCD с вершиной в точке D . Найти:

а) площадь грани ABC ;

б) объем пирамиды ABCD ;

в) уравнения ребер AD и BD , указав координаты направляющих векторов;

г) уравнения граней ABC и ABD , указав координаты их нормалей; д) длину высоты DK ;

е) угол между плоскостью основания ABC и боковым ребром AD;

- 50 -

Линейная алгебра	Типовые расчеты

аналитическая геометрия	методические указания

ж) угол между плоскостью основания ABC и боковой гранью ABD ; з) уравнение плоскости, проходящей через вершину D параллельно

основанию ABC ;

и) уравнение прямой, проходящей через точку C параллельно ребру

AD;

к) уравнение прямой, проходящей через точку A перпендикулярно плоскости основания ABC ;

л) угол между боковыми ребрами AD и BD .

1. A 2; 1; 1 ; B 5; 1; 2 ; C 3; 0; 3 ; D 6; 0; 1 . 2. A 4;1; 3 ; B 0;1; 2 ; C 2; 3; 2 ; D 1; 3; 0 . 3. A 2; 2; 0 ; B 1; 2; 5 ; C 3; 3; 1 ; D 1; 4; 3 .

4. A 1; 2;1 ; B 0; 1; 5 ; C 4; 0;1 ; D 2;1; 3 .

5.	A 5; 1; 2 ; B 2; 1; 2 ; C 1; 0; 5 ; D 1; 1; 4 .
6. A 2;1; 2 ; B 3; 3; 3 ; C 1;1; 2 ; D 1; 2; 3 .
7.	A 5;1; 4 ; B 1; 2; 1 ; C 3; 3; 4 ; D 2; 2; 2 .
8.	A 3;1; 0 ; B 0; 7; 2 ; C 1; 0; 5 ; D 4;1; 5 .
9.	A 0; 0; 2 ; B 3; 0; 5 ; C 1; 1; 0 ; D 4; 1; 2 .
10.	A 7; 3; 2 ; B 0; 2;1 ; C 4; 1; 0 ;		D 1; 0; 3 .
11.	A 3; 1; 0 ;	B 0; 1; 2 ; C 1; 0; 5 ;	D 4; 5; 1 .
12.	A 0; 0; 1	; B 1; 3; 4 ; C 5; 0; 3 ;	D 4; 4; 1 .

14.

15.

13. A 1; 2; 5 ; B 0; 4; 5 ; C 3; 2;1 ; D 1; 2; 4 .

- 51 -

Линейная алгебра										Типовые расчеты

аналитическая геометрия									методические указания
16.	A 5; 1; 4 ;		B 9; 3; 6 ;		C 7;10; 14 ;				D 5;1; 3 .
17.	A 1; 4; 0 ;	B 5; 0; 2 ;		C 3; 7; 10 ;				D 1; 2;1 .
18.	A 3; 6; 2 ;		B 1; 2; 0 ;		C 1; 5; 8 ;			D 3; 4; 3 .
19.	A 1;1; 5 ; B 3; 5; 7 ;				C 1;12; 15 ;			D 1; 3; 4 .
20.	A 4; 2; 1 ;		B 0; 6; 3 ;		C 2;13; 11 ;				D 4; 4; 0 .
21.	A 0; 4; 3 ;	B 4; 8; 1 ; C 2; 15; 7 ;					D		0; 6; 4 .
22.	A 2; 0; 2 ;		B 2; 4; 4 ; C 0;11; 12 ;						D 2; 2; 1 .
23.	A 3; 3; 3 ;	B 7; 7; 5 ;		C 5;14; 13 ;				D 3; 5; 2 .
24.	A 4; 2; 5	;	B 8; 2; 3 ;	C 6; 9; 5 ;			D 4; 0; 6			.
25.	A 5; 0;1 ;	B 4; 2; 3 ;			C 6; 2;11 ; D 3; 4; 9					.
26.	A 3; 4; 3 ;		B 2; 2; 1 ;			C 8; 6; 7	;	D 5; 8; 5 .
27.	A 2; 3; 2 ;		B 1; 5; 4 ;			C 9; 1;12 ;			D 6;1;10 .
28.	A 4; 5; 5 ;		B 3; 3; 3 ;			C 7; 7; 5 ;		D 4; 9; 3 .
29.	A 2; 1; 4 ;		B 3; 3; 2		;	C 13;1; 6	;	D 10; 3; 4 .
30.	A 8; 3; 1 ;		B 7; 1; 1 ;		C 3; 5; 9 ;		D 0; 7; 7			.

Решение типового примера.

Пусть даны координаты вершин пирамиды ABCD :

A 5; 3; 9 ; B 5; 3; 3 ; C 1; 1; 5 ; D 1; 1; 9 .

а) Вычислить площадь грани ABC .

Для вычисления площади грани ABC , используем определяющую площадь треугольника, построенного на a и b :

S		1	a b	,
		1

	2
	2
	- 52 -

формулу

векторах

10.1

Линейная алгебра		Типовые расчеты

аналитическая геометрия		методические указания
где a b	векторное произведение векторов	a a x ; a y ; a x и

b bx ; by ; bz , которое может быть найдено следующим образом:

	i	j	k
a b	a x	a y	a x	.
	bx	b y	bz

В нашем случае, грань ABC , можно определить как треугольник, построенный на векторах AB и AC . Значит формула (10.1) примет вид:

S	ABC		1	AB AC	.


		2

Найдем координаты необходимых векторов AB , AC и их векторное произведение.

AB 5 5; 3 3; 3 9 0; 6; 6 ;

AC 1 5; 1 3; 5 9 4; 2; 4 .

Тогда:
	i	j	k		6	6		0 6			0 6


AB AC	0	6	6	i			j			k
	4	2	4		2	4		4	4		4 2
	4	2	4

i 24 12 j 0 24 k 0 24 12 i 24 j 24 k .

Далее, найдем длину вектора, равного векторному произведе-

нию AB AC :


				12 2 24 2 24 2 12
AB AC				12 2 24 2 24 2 12					12 2 2 2 2	12	9 36
Таким образом, площадь грани ABC , равна:
S	ABC		1		AB AC		1	36 18 кв. ед. .
			1				1

		2				2
		2				2
				- 53 -

Линейная алгебра	Типовые расчеты

аналитическая геометрия	методические указания

б) Вычислить объѐм пирамиды ABCD .
Объѐм пирамиды, построенной на векторах					a ; b ; c можно
вычислить по формуле:
V			1	a b c ,	10.2
	пир.
		6

где
a b c — смешанное произведение векторов					a a x ; a y ; a x ,
b bx ; by ; bz и c c x ; c y ; c z ,				которое можно вычислить сле-

дующим образом:
	a x	a y	a x
	a x	a y	a x
a b c	bx	b y	bz	.
	c x	c y	c z

В нашем случае, пирамида ABCD, можно рассматривать как

пирамиду, построенную на векторах AB , AC и AD .

Вычислим смешанное произведение этих векторов. Для этого

найдем координаты вектора AD :

AD 1 5; 1 3; 9 9 4; 2; 0 .

		6	6
	0	6	6
AB AC AD	4	2	4	0 96 48 48 0 0 96 .
	4	2	0

Таким образом, объем пирамиды ABCD :

V ABCD 16 96 16 куб. ед. .

в) Найти уравнения ребер AD и BD , указав координаты направляющих векторов.

- 54 -

Линейная алгебра																				Типовые расчеты

аналитическая геометрия																			методические указания
Уравнение ребра можно найти как уравнение прямой, прохо-
дящей через две заданные точки M 1 x1;															y1; z1			и M 2 x2 ; y 2 ; z 2 по
формуле:
						x x1						y y1			z z1		,				10.3
																	,				10.3
					x2 x1						y 2 y1			z 2 z1
где s x2 x1;			y2 y1; z 2					z1 направляющий вектор прямой.
В нашем случае:
AD :		x 5		y 3				z 9		;			x 5			y 3				z 9	; z 9 0.
AD :		1 5	1 3					9 9		;			4		2				0		; z 9 0.
		1 5	1 3					9 9					4		2				0
Направляющий вектор соответственно:														s AD 4; 2; 0 .
BD :		x 5		y 3				z 3	;				x 5			y 3				z 3	;
BD :		1 5	1 3				9 3		;				4			4			6		;
		1 5	1 3				9 3						4			4			6
		x 5		y 3				3 z			.
											.
	2		2					3

Направляющий вектор: s BD 2; 2; 3 .

г) Найти уравнения граней ABC и ABD , указав координаты их нормалей.

Уравнение грани можно определить как уравнение плоскости,

проходящей через три заданные точки M 1 x1; y1; z1 ,					M 2 x2 ; y2 ; z2
и M 3 x3 ; y3 ; z3 по следующей формуле:
	x x1	y y1	z z1		10.4
	x x1	y y1	z z1
	x2 x1	y 2 y1	z 2 z1	0
	x3 x1	y3 y1	z 3 z1

Внашем случае, по формуле (10.4) получим:

-55 -

Линейная алгебра						Типовые расчеты

аналитическая геометрия						методические указания
ABC :	x 5	y 3	z 9		x 5	y 3	z 9
	x 5	y 3	z 9		x 5	y 3	z 9
	5 5	3 3	3 9	0 ;	0	6	6	0 ;
	1 5	1 3	5 9		4	2	4

x 5 24 12 y 3 0 24 z 9 0 24 0;

12 x 5 24 y 3 24 z 9 0;

x 5 2 y 3 2 z 9 0;

x 5 2y 6 2z 18 0;					x 2 y 2z 7 0			ABC


Аналогично, найдем уравнение грани ABD .
ABD :	x 5	y 3	z 9			x 5	y 3	z 9
	x 5	y 3	z 9			x 5	y 3	z 9
	5 5	3 3	3 9	0 ;		0	6	6	0 ;
	1 5	1 3	9 9			4	2	0

x 5 0 12 y 3 0 24 z 9 0 24 0;

12 x 5 24 y 3 24 z 9 0;

1 x 5 2 y 3 2 z 9 0;

x 5 2y 6 2z 18 0; x 2 y 2z 17 0 ABD

д) Найти длину высоты DK .

Длину высоты пирамиды определим из формулы для нахождения объѐма пирамиды, а именно:

Vпир. 13 S основ. h,

где h длина высоты, опущенной на основание пирамиды.

В нашем случае: V ABCD 13 S ABC DK .

Выразим отсюда искомую длину высоты:

- 56 -

Линейная алгебра										Типовые расчеты

аналитическая геометрия										методические указания
						DK			3 V ABCD	.
									3 V ABCD

									S ABC
									S ABC
В пункте а) и б) были вычислены соответствующие значения
площади грани ABC S ABC 18 и объѐм пирамиды											VABCD 16 .
Тогда, длина высоты DK, составит:
	DK		3 16	48			8	лин. ед. .
			3 16	48			8

		18		18	3
		18		18	3

Замечание. Длину высоты DK, можно также определить как расстояние от точки D до плоскости ABC по формуле:

A x0

B y 0 C z 0 D

A 2 B 2 C 2

где

Ax By Cz D – уравнение плоскости, x0 ; y 0 ; z 0 – координаты точки.

В нашем случае:

1 1 2 1 2 9 7

лин. ед. .

12 2 2 2 2

е)

Вычислить значение угла между плоскостью основания ABC и

боковым ребром AD.

За угол между прямой и плоскостью принимают угол между

этой прямой и еѐ проекцией на данной плоскость. Он может быть вычислен по формуле:

sin

n s

где n A; B; C

s m; n; p

нормальный вектор плоскости,

направляющий вектор прямой.

Эту формулу можно записать в координатном виде:

sin			A m B n C p		.
			A m B n C p


	A 2	B 2 C 2		m 2 n 2 p 2
	A 2	B 2 C 2		m 2 n 2 p 2
		- 57 -

Линейная алгебра	Типовые расчеты

аналитическая геометрия	методические указания
В нашем случае, плоскость	ABC имеет следующее уравне-

ние: x 2y 2z 7 0 , значит, еѐ нормальный вектор имеет коор-

динаты n 1; 2; 2 . А ребро AD имеет направляющий вектор

s AD 4; 2; 0 (см. пункты в) и г)). Тогда получим:
sin		1 4 2 2 2 0					4 4		8	,
		1 4 2 2 2 0					4 4		8


	12 2 2		2 2		4 2 2 2 0 2		9
	12 2 2		2 2		4 2 2 2 0 2		9	20 3 20
или
	sin		8	0,6 arcsin 0,6		37 o .



	3		20

ж) Вычислить значение угла между плоскостью основания ABC и боковой гранью ABD .

За угол между двумя плоскостями можно принять угол между их нормальными векторами, который может быть вычислен по

формуле:
	cos n 1; n 2					n 1 n 2			.
						n 1	n 2


В нашем случае нормальные вектора плоскостей ABC и ABD
имеют координаты: n ABC 1; 2; 2 и n ABD 1; 2; 2 , тогда:
cos n ABC ; n ADD				1 1	2 2 2 2							7		,


		12 2 2 2 2										9	9
								12 2 2 2 2
								12 2 2 2 2
или
			7							7
cos n ABC ; n ADD				n ABC ; n ADD			arccos				2, 462 .
cos n ABC ; n ADD			9	n ABC ; n ADD			arccos			9	2, 462 .
			9							9

з) Найти уравнение плоскости, проходящей через вершину D параллельно основанию ABC .

- 58 -

Линейная алгебра	Типовые расчеты

аналитическая геометрия	методические указания
Пусть Ax By Cz D 0	уравнение искомой плоскости P .

По условию плоскость P параллельна плоскости ABC . Используем условие параллельности плоскостей: две плоскости параллельны,

если координаты их нормальных векторов пропорциональны, т. е.

P \|\| P n			\|\| n		A1	B1	C1	.
		1		2
1	2				A2	B2	C2

В нашем случае, нормальный вектор плоскости ABC имеет координаты n ABC 1; 2; 2 . Поскольку искомая плоскость па-

раллельна плоскости ABC , то 1, а значит, координаты нор-

мального вектора искомой плоскости также: n P 1; 2; 2 . То

есть уравнение плоскости P имеет вид:

x 2 y 2 z D 0.

Также по условию известно, что плоскость P, проходит через точку D, а значит, координаты этой точки должны удовлетворять уравнению плоскости, т. е.

1 2 1 2 9 D 0; D 15.

Окончательно, уравнение плоскости P, параллельной грани ABC , имеет вид: x 2 y 2z 15 0 .

и) Найти уравнение прямой, проходящей через точку C параллельно ребру AD.

Используем формулу, определяющую канонические уравне-

ния прямой в пространстве:
		x x1		y y1	z z1	,	10.5
		m		n	p	,	10.5
		m		n	p
где x1; y1; z1	координаты		произвольной точки прямой,				m; n; p

координаты любого еѐ направляющего вектора.

-59 -

Линейная алгебра	Типовые расчеты

аналитическая геометрия	методические указания

Поскольку искомая прямая l , по условию, параллельна прямой AD, то в качестве еѐ направляющего вектора, может быть взят направляющий вектор ребра AD: s l s AD 4; 2; 0 .

Также, по условию, прямая l , проходит через вершину C, то по формуле (10.5) имеем:

	x 1	y 1		z 5	;	z 5 0	l .

	4	2	0					A перпенди-

к) Найти уравнение прямой,			проходящей через точку
кулярно плоскости основания ABC .

Как и в предыдущем пункте, используем канонические уравнения прямой в пространстве (10.5). Точка A точка прямой, а в качестве направляющего вектора искомой прямой g возьмем нормальный вектор плоскости ABC : n ABC 1; 2; 2 . Получим:

	x 5		y 3					z 9		;		10 2x y 3 z 9								g .
1			2					2		;		10 2x y 3 z 9								g .



л) Вычислить значение угла между боковыми ребрами AD и BD .
Угол между двумя прямыми l1													и l 2 определим как угол между
их направляющими векторами s 1 m1; n1;															p1			и s 2	m2 ; n2 ; p2
по формуле:
	cos		s1 s			2					m1 m2 n1 n			2 p1 p 2							.


			s	1	s		2		m 2			n 2	p 2			m 2		n 2 p 2
				1			2			1		1	1	2				2	2
В нашем случае,						s 1 s AD 4; 2; 0 , s 2 s BD 2; 2; 3 , тогда:
cos				4 2 2 2 0 3														4		0,22 .



		4 2 2 2 0 2									2 2 2 2 33						20 17

Откуда, arccos 0, 22 1,39.

- 60 -

<<< < Предыдущая 1 2 34 / 54 5 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
21.05.2015628.74 Кб75методичка УФ.doc
#
21.05.2015925.94 Кб28Методичка ФВ для очников.docx
#
21.05.2015874.59 Кб39Методичка фин. выч. для очников.docx
#
21.05.2015675.84 Кб35методичка.doc
#
21.05.2015850.94 Кб52Методичка.doc
#
20.03.20162.03 Mб53Методичка_.pdf
#
21.05.2015570.88 Кб58методичка_организационное_проектирование.docx
#
21.05.2015784.38 Кб35Методуказания.doc
#
26.04.201910.85 Mб29Метрология.doc
#
21.05.20156.43 Mб351Механизация послеуборочной обработки зерна.pdf
#
21.05.201530.21 Mб2618Механизация часть вторая.doc