Как найти уравнение касательной и уравнение нормали, если функция задана неявно?
Формулы касательной и нормали остаются прежними, но меняется техника решения:
Пример 6
Найти уравнения касательной и нормали к кривой 
в точке 
.
Решение: судя по уравнению, это какая-то линия 3-го порядка, какая именно – нас сейчас совершенно не интересует.
В уравнении присутствует зловред 
, и поэтому перспектива выразить функция в явном виде 
выглядит весьма туманной.
Но этого и не требуется! Есть куда более остроумное решение. Уравнение касательной составим по той же формуле
.
Из условия известны значения 
, кстати, не помешает убедиться, что они действительно удовлетворяют предложенному уравнению:
Получено верное равенство, значит, с точкой 
всё в порядке.
Осталось вычислить 
. Сначала по стандартной схеме найдём производную от функции, заданной неявно:
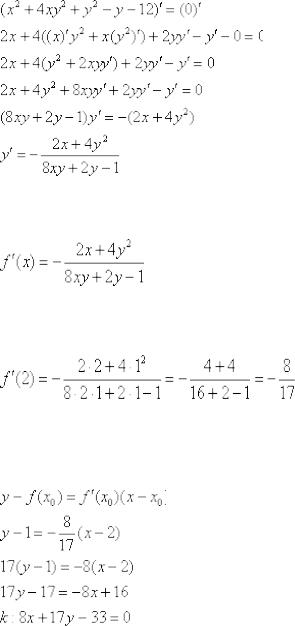
Перепишем результат с более подходящим для нашей задачи обозначением:
На 2-м шаге в найденное выражение производной подставим 
:
Вот так-то!
Осталось аккуратно разобраться с уравнением:
Составим уравнение нормали:
Ответ: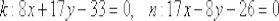 
Готово! А поначалу представлялось всё непросто. Хотя производная здесь, конечно, – место уязвимое. Миниатюра для самостоятельного решения:
Пример 7
Найти уравнение нормали к линии 
в точке
Хватит уже вымучивать касательную =)
В данном случае легко выяснить, что это окружность 
центром в точке 
радиуса 
и даже выразить нужную функцию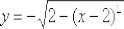 
. Но зачем?! Ведь найти производную от неявно
заданной функции на порядок легче! Она тут чуть ли не самая примитивная.
Краткое решение и ответ в конце урока.
Как найти уравнение касательной и уравнение нормали, если функция задана параметрически?
Ещё проще. Но для этого нужно потренироваться в нахождении
производной от параметрически заданной функции. А так – почти халява:
Пример 8
Составить уравнения касательной и нормали к циклоиде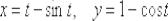 
, проведенные в точке, для которой 
.
Чертёж циклоиды можно найти на странице S и V, если линия задана параметрически (так получилось, что эта статья была создана раньше). Там даже изображена точка касания.
Решение: абсцисса и ордината точки касания рассчитываются непосредственно из параметрических уравнений кривой:
Найдём 1-ую производную от параметрически заданной функции:
И вычислим её значение при 
:
Уравнение касательной составим по обычной формуле с поправкой на несколько другие обозначения:
Уравнение нормали:
Ответ: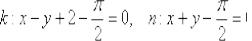 
В заключение предлагаю познакомиться с ещё одной интересной
линией: Пример 9
Составить уравнение нормали к полукубической параболе 
, проведенной в точке, для которой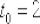 
.
Это пример для самостоятельного решения. Напоминаю, что графики параметрически заданных функций можно построить, например, с помощью моего расчётного геометрического макета.
Ну а наш урок подошёл к концу, и я надеюсь, что изложенный материал прошёл для вас не по касательной, а нормально =)
Спасибо за внимание и успехов!
Решения и ответы:
Пример 2: Решение: уравнение касательной составим по формуле:
В данном случае:
Таким образом:
Уравнение нормали составим по формуле 
:
Ответ:
Пример 4: Решение: уравнение касательной составим по формуле:
В данной задаче:
Таким образом:
В точке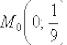 
касательная параллельна оси 
, поэтому соответствующее уравнение нормали:
Ответ: 
Пример 7: Решение: в данной задаче: 
. Найдём производную:
Или:
Подставим в выражение производной 
:
Искомое уравнение нормали:
Ответ: 
Пример 9: Решение: в данном случае:
Найдём производную и вычислим её значение при 
:
Уравнение нормали:
Ответ: 