
- •Как найти производную? Примеры решений
- •Производная сложной функции. Примеры решений
- •Сложные производные
- •Логарифмическая производная
- •Производная степенно-показательной функции
- •Производная функции, заданной неявно
- •Производная параметрически заданной функции
- •Простейшие типовые задачи с производной. Примеры решений
- •Производная функции в точке
- •Уравнение касательной к графику функции
- •Как составить уравнение касательной в точке с абсциссой ?
- •Дифференциал функции одной переменной
- •Вторая производная
- •Производные высших порядков
- •производным высших порядков от произведения функций
- •Формула Лейбница
- •Производные высших порядков от функций, заданных неявно
- •Что такое производная? Определение и смысл производной функции
- •Понятие возрастания, убывания, максимума, минимума функции
- •Скорость изменения функции
- •Производная функции в точке
- •Геометрический смысл производной
- •Существование производной в точке и непрерывность функции
- •Дифференциал функции в точке и его геометрический смысл
- •Понятие производной функции
- •Производная по определению (через предел). Примеры решений
- •Как найти производную по определению?
- •Как найти уравнение нормали к графику функции в заданной точке?
- •Как найти уравнение касательной и уравнение нормали, если функция задана неявно?
- •Как найти уравнение касательной и уравнение нормали, если функция задана параметрически?
- •Приближенные вычисления с помощью дифференциала
- •Приближенные вычисления с помощью дифференциала функции одной переменной
- •Абсолютная и относительная погрешность вычислений
- •Приближенные вычисления с помощью полного дифференциала функции двух переменных
- •Метод касательных
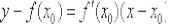
Как найти уравнение нормали к графику функции в заданной точке?
На данном уроке мы узнаем, как найти уравнение нормали к графику функции 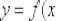 в точке
в точке  и разберём многочисленные
и разберём многочисленные
примеры, которые касаются этой задачи. Для качественного усвоения материала нужно понимать геометрический смысл производной и
уметь их находить хотя бы на уровне следующих статей:
Как найти производную? Производная сложной функции
и
Простейшие задачи с производными.
Перечисленные уроки позволят «чайникам» быстро сориентироваться в теме и поднять свои навыки дифференцирования практически с полного нуля. По существу, сейчас последует развёрнутое продолжение параграфа об уравнении касательной 3-й статьи из вышеприведенного списка. Почему продолжение? Уравнение нормали тесно связано с уравнением касательной. Помимо прочего я рассмотрю задачи о том, как построить уравнения этих линий в ситуациях, когда функция задана неявно либо параметрически.
Но сначала освежим воспоминания: если функция  дифференцируема в точке
дифференцируема в точке  (т.е. если существует конечная производная
(т.е. если существует конечная производная  ), то уравнение касательной к графику функции в точке
), то уравнение касательной к графику функции в точке  можно найти по следующей формуле:
можно найти по следующей формуле:

Это самый распространенный случай, с которым мы уже столкнулись на уроке Простейшие задачи с производными. Однако дело этим не
ограничивается: если в точке  существует бесконечная производная:
существует бесконечная производная:  , то касательная будет параллельна оси
, то касательная будет параллельна оси  и её уравнение примет вид
и её уравнение примет вид  . Дежурный пример: функция
. Дежурный пример: функция  с
с
производной  , которая обращается в бесконечность
, которая обращается в бесконечность
вблизи критической точки  . Соответствующая касательная выразится уравнением:
. Соответствующая касательная выразится уравнением:
(ось ординат).
Если же производной  не существует (например, производной от
не существует (например, производной от 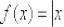 в точке
в точке  ), то, разумеется, не существует и общей касательной.
), то, разумеется, не существует и общей касательной.
Как различать последние два случая, я расскажу чуть позже, а пока что вернёмся в основное русло сегодняшнего урока:
Что такое нормаль? Нормалью к графику функции  в точке
в точке  называется прямая, проходящая через данную точку перпендикулярно касательной к графику функции в этой точке
называется прямая, проходящая через данную точку перпендикулярно касательной к графику функции в этой точке
(понятно, что касательная должна существовать). Если совсем коротко, нормаль – это перпендикулярная к касательной прямая, проходящая через точку касания.
Как найти уравнение нормали? Из курса аналитической геометрии напрашивается очень простой алгоритм: находим
уравнение касательной и представляем его в общем виде
 . Далее «снимаем» нормальный вектор
. Далее «снимаем» нормальный вектор  и составляем уравнение нормали по точке
и составляем уравнение нормали по точке  и направляющему вектору
и направляющему вектору  .
.
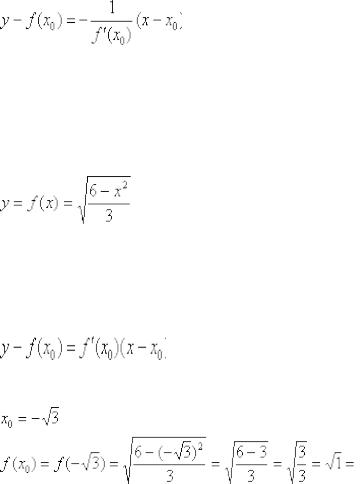
Этот способ применять можно, но в математическом анализе принято пользоваться готовой формулой, основанной на взаимосвязи угловых коэффициентов перпендикулярных прямых. Если
существует конечная и отличная от нуля производная 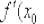 , то уравнение нормали к графику функции
, то уравнение нормали к графику функции  в точке
в точке  выражается следующим уравнением:
выражается следующим уравнением:
Особые случаи, когда  равна нулю либо бесконечности мы обязательно рассмотрим, но сначала «обычные» примеры:
равна нулю либо бесконечности мы обязательно рассмотрим, но сначала «обычные» примеры:
Пример 1 Составить уравнения касательной и нормали к графику кривой
в точке, абсцисса которой равна  .
.
В практических заданиях часто требуется найти и касательную тоже. Впрочем, это очень только нА руку – лучше будет «набита рука» =)
Решение: Первая часть задания хорошо знакома, уравнение касательной составим по формуле:
В данном случае:
Найдём производную:
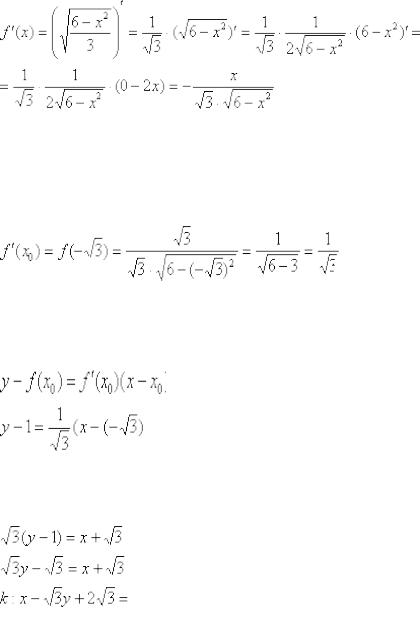
Здесь на первом шаге вынесли константу за знак производной, на втором – использовали правило дифференцирования сложной функции.
Теперь вычислим производную в точке  :
:
Получено конечное число и это радует. Подставим  и
и  в формулу
в формулу
:
Перебросим  наверх левой части, раскроем скобки и представим уравнение касательной в общем виде:
наверх левой части, раскроем скобки и представим уравнение касательной в общем виде:
Вторая часть задания ничуть не сложнее. Уравнение нормали составим по формуле:
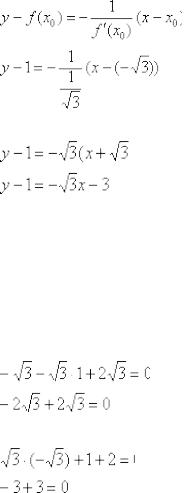
Избавляемся от трёхэтажности дроби и доводим уравнение до ума:
 – искомое уравнение.
– искомое уравнение.
Ответ: 
Здесь можно выполнить частичную проверку. Во-первых, координаты точки  должны удовлетворять каждому уравнению:
должны удовлетворять каждому уравнению:
 – верное равенство.
– верное равенство.
 – верное равенство.
– верное равенство.
И, во-вторых, векторы нормали 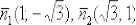 должны быть
должны быть
ортогональны. Это элементарно проверяется с помощью скалярного произведения:
 , что и требовалось проверить.
, что и требовалось проверить.
Как вариант, вместо нормальных векторов можно использовать
направляющие векторы прямых.

! Данная проверка оказывается бесполезной, если неверно найдена производная  и/или производная в точке
и/или производная в точке  . Это «слабое звено» задания – будьте предельно внимательны!
. Это «слабое звено» задания – будьте предельно внимательны!
Чертежа по условию не требовалось, но полноты картины ради:
Забавно, но фактически получилась и полная проверка, поскольку чертёж выполнен достаточно точно =) Кстати, функция
 задаёт верхнюю дугу эллипса. Следующая задача для самостоятельного решения:
задаёт верхнюю дугу эллипса. Следующая задача для самостоятельного решения:
Пример 2 Составить уравнения касательной и нормали к графику функции
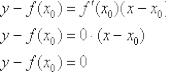
 в точке
в точке  .
.
Примерный образец чистового оформления задания в конце урока. Теперь разберём два особых случая:
1) Если производная в точке  равна нулю:
равна нулю:  , то уравнение касательной упростится:
, то уравнение касательной упростится:
То есть, касательная будет параллельна оси  . Соответственно, нормаль будет проходить через точку
. Соответственно, нормаль будет проходить через точку 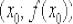
параллельно оси  , а значит её уравнение примет вид
, а значит её уравнение примет вид  .
.
2) Если производная в точке  существует, но бесконечна:
существует, но бесконечна:  , то, как отмечалось в самом начале статьи, касательная станет вертикальной:
, то, как отмечалось в самом начале статьи, касательная станет вертикальной:  . И поскольку нормаль проходит через точку
. И поскольку нормаль проходит через точку 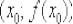 параллельно оси
параллельно оси  , то её уравнение выразится «зеркальным» образом:
, то её уравнение выразится «зеркальным» образом:  Всё просто:
Всё просто:
Пример 3
Составить уравнения касательной и нормали к параболе 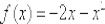 в точке
в точке  . Сделать чертёж.
. Сделать чертёж.
Требование выполнить чертёж я не добавлял – так было сформулировано задание в оригинале. Хотя это редкость.
Решение: составим уравнение касательной  .
.

В данном случае 
Казалось бы, расчёты пустяковые, а в знаках запутаться более чем реально:
Таким образом:
Поскольку касательная параллельна оси  (Случай №1), то нормаль, проходящая через ту же точку
(Случай №1), то нормаль, проходящая через ту же точку  , будет параллельна оси ординат:
, будет параллельна оси ординат:
Чертёж – это, конечно же, дополнительные хлопоты, но зато добротная проверка аналитического решения:
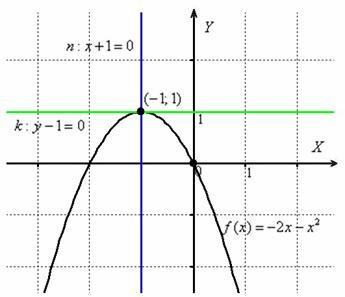
Ответ:  ,
, 
В школьном курсе математики распространено упрощённое определение касательной, которое формулируется примерно так:
«Касательная к графику функции – это прямая, имеющая с данным графиком единственную общую точку». Как видите, в общем случае это утверждение некорректно. Согласно геометрическому смыслу производной, касательной является именно зелёная, а не синяя прямая.
Следующий пример посвящён тому же Случаю №1, когда  : Пример 4
: Пример 4
Написать уравнение касательной и нормали к кривой  в точке
в точке  .
.
Краткое решение и ответ в конце урока

Случай №2, в котором  на практике встречается редко, поэтому начинающие могут особо не волноваться и с лёгким сердцем пропустить пятый пример. Информация, выделенная курсивом, предназначена для читателей с высоким уровнем подготовки, которые хорошо разобрались с определениями производной и касательной, а также имеют опыт нахождения производной по определению:
на практике встречается редко, поэтому начинающие могут особо не волноваться и с лёгким сердцем пропустить пятый пример. Информация, выделенная курсивом, предназначена для читателей с высоким уровнем подготовки, которые хорошо разобрались с определениями производной и касательной, а также имеют опыт нахождения производной по определению:
Пример 5 Найти уравнения касательной и нормали к графику функции
 в точке
в точке 
Решение: в критической точке  знаменатель производной
знаменатель производной  обращается в ноль, и поэтому здесь нужно
обращается в ноль, и поэтому здесь нужно
вычислить односторонние производные 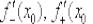 с помощью определения производной (см. конец статьи Производная по определению):
с помощью определения производной (см. конец статьи Производная по определению):
Обе производные бесконечны, следовательно, в точке 
существует общая вертикальная касательная:
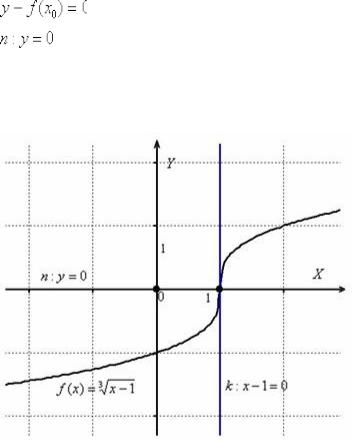
Ну, и очевидно, что нормалью является ось абсцисс. Формально по формуле:
Для лучшего понимания задачи приведу чертёж:
Ответ: 
Я рад, что вы не ушли бороздить просторы Интернета, потому что всё самое интересное только начинается! Чтобы осилить материал следующего параграфа, нужно уметь находить производную от неявно заданной функции:
