
- •Мультимедийные лекции
- •Содержание
- •Основные сведения о матрицах.
- •Виды матриц
- •Операции над матрицами и их свойства.
- •Правило Саррюса (правило треугольника).
- •Теорема Лапласа
- •Свойства определителей.
- •Вырожденные и невырожденные матрицы, обратная матрица.
- •Решение матричных уравнений.
- •Ранг матрицы, нахождение ранга матрицы.
- •Элементарные преобразования матрицы.
- •Системы линейных алгебраических уравнений слу (Основные понятия и определения).
- •Методы решения систем линейных уравнений.
- •1) Метод обратной матрицы (матричный метод) решения систем n линейных уравнений с n неизвестными.
- •2) Правило Крамера решения систем n – линейных уравнений с n – неизвестными.
- •Метод Гаусса решения систем линейных уравнений.
- •Исследование систем линейных уравнений. Теорема Кронекера - Капелли, базисные решения.
- •Системы линейных однородных уравнений. Исследование решений. Фундаментальная система решений.
- •Модель Леонтьева многоотраслевой экономики. Продуктивные модели Леонтьева.
- •Балансовые соотношения
- •Линейная модель многоотраслевой экономики
- •Векторы (основные понятия и определения).
- •Сложение векторов
- •Разность векторов
- •Линейные операции над векторами. Направляющие косинусы.
- •Прямоугольный базис.
- •Декартова прямоугольная система координат в пространстве.
- •Прямоугольные координаты вектора (точки).
- •Разложение вектора по базису.
- •Формулы для нахождения длины вектора, расстояния между точками и угла между векторами.
- •Векторное произведение векторов (геометрический смысл, свойства).
- •Свойства векторного произведения.
- •Выражение векторного произведения через координаты.
- •Смешанное произведение векторов (геометрический смысл, свойства).
- •Выражение векторного и смешанного произведения через координаты перемножаемых векторов.
- •Уравнение плоскости, проходящей через три данные точки.
- •Понятие векторного (линейного) пространства. Вектор вn‒ мерном пространстве.
- •Размерность и базис векторного пространства.
- •Линейная оболочка и ее свойства.
- •Свойства линейной оболочки
- •Евклидово пространство.
- •Ортогональный и ортонормированный базис.
- •Переход к новому базису.
- •Линейные операторы.
- •Собственные векторы и собственные значения линейного оператора (матрицы).
- •Квадратичные формы.
- •Линейная модель обмена (международной торговли).
- •Уравнения прямой (различные виды). Параметрические уравнения прямой.
- •Уравнение прямой проходящей через две данные точки.
- •Угловой коэффициент прямой. Уравнение прямой, проходящей через данную точку с данным угловым коэффициентом.
- •Уравнение прямой, проходящей через данную точку с данным нормальным вектором (нормалью).
- •Общее уравнение прямой.
- •Формула угла между прямыми.
- •Условия параллельности и перпендикулярности прямых.
- •Формула расстояния от точки до прямой.
- •Комплексные числа. Алгебраическая форма комплексного числа.
- •Действия над комплексными числами в алгебраической форме.
Векторы (основные понятия и определения).
Все величины делятся на скалярные и векторные.
Скалярные величины характеризуются числовым значением (вес товара, стоимость и т.д.)
Векторные величины характеризуются числовым значением и направлением.
Вектором называется направленный отрезок, на котором указаны начало, конец и направления.

Обозначается
 или
или ,
, ‒
длина вектора.
‒
длина вектора.
Векторы называются коллинеарными, если их направление совпадает или противоположно.
|
а) б) |
|
 ‒коллинеарные.
‒коллинеарные.
Теорема. Признак коллинеарности векторов.
Для
того чтобы
 былколлинеарен
ненулевому
былколлинеарен
ненулевому необходимо и достаточно, чтобы существовало
такое числоk,
для
которого выполнялось бы равенство:
необходимо и достаточно, чтобы существовало
такое числоk,
для
которого выполнялось бы равенство:
 =
k
=
k ,
,
где k– коэффициент пропорциональности.
Векторы
 называются компланарными,
если их можно поместить в одну плоскость
путем параллельного переноса.
называются компланарными,
если их можно поместить в одну плоскость
путем параллельного переноса.
Сложение векторов
Правило треугольника

![]()
Правило параллелограмма

Разность векторов
 =
=

Линейные операции над векторами. Направляющие косинусы.
Положение вектора в пространстве задают направляющие Cos углов (, , j) вектора с осями координат:
Cos
= ;
Cos
=
;
Cos
= ;
Cos
j
=
;
Cos
j
= ;
;
Пусть =
(
=
( );
); = (
= ( );
);
1. Сумма (разность) векторов:
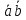 =
(
=
(
(
( = (
= ( )
) + (
+ ( + +(
+ +( =(
=( ;
;
 .
.
2. Умножение вектора на:
·
 = (
= ( ;
;
 ;
;
 ).
).
3. Скалярное произведение векторов и его свойства.
Скалярным произведением векторов называется число равное произведению длин этих векторов на косинус угла между ними.
 =
=
 ·Cos;
·Cos;
где
=( );
);
 ≤ ≤
≤ ≤
Свойства:
1.
 =
=
 =
=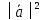 –скалярный
квадрат.
–скалярный
квадрат.
2.
Если
 ,
то
,
то
 = 0;
т.к. Cos
= 0;
т.к. Cos =
0;
=
0;
3.
 =
=
 ‒
коммутативность
‒
коммутативность
4.
( = (
= ( )
)
 =
= (·
(· –ассоциативность
–ассоциативность
5.
( )
) =
= +
+ ·
· –дистрибутивность
–дистрибутивность
Выведем формулу скалярного произведения через координаты:
 =
(
=
( · (
· ( =
= +
+ +
+
 +
+ +
+ +
+ +
+ +
+ +
+ =
=
=
 +
+
 +
+
 =
=
 +
+
 +
+
– формула для нахождения скалярного произведения.
Прямоугольный базис.
Декартова прямоугольная система координат в пространстве.
Прямоугольные координаты вектора (точки).
Разложение вектора по базису.
При
взаимных перпендикулярных единичных
вектора
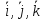 ,
выходящих из одной точки, образуют
прямоугольный базис в пространстве.
,
выходящих из одной точки, образуют
прямоугольный базис в пространстве.
Прямые проведенные в направлении базисных векторов образуют прямоугольную декартову систему координат:
ОХ
– в направлении ‒
 ‒ ось абсцисс;
‒ ось абсцисс;
ОУ
– в направлении ‒
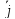 ‒ ось ординат;
‒ ось ординат;
ОZ
– в направлении ‒
 ‒ ось аппликат;
‒ ось аппликат;

 ‒орты
координаты осей, т.е.
‒орты
координаты осей, т.е.
 ‒
орт оси ОХ и т.д.
‒
орт оси ОХ и т.д.
 =
OM
– радиус ‒
вектор
точки М.
=
OM
– радиус ‒
вектор
точки М.
 ;
; =
1.
=
1.
Прямоугольными координатами вектора (точки) называются проекции этого вектора (точки) на оси ординат.
 =
(x,
y,
z).
=
(x,
y,
z).
 =
=
 =
= +
+
 =
= +
+ +
+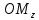 = х
= х + у
+ у +z
+z
 =
х
=
х + у
+ у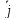 +z
+z
‒ разложение
вектора
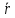 по базису
по базису
Формулы для нахождения длины вектора, расстояния между точками и угла между векторами.
По свойству длинны диагонали прямоугольного треугольника, получим:
 2
=
2
=
 2
=
2
=
 2
+
2
+
 2
+
2
+
 2,
2,
т. е.
 2
=
x2
+
y2
+
z,
2
=
x2
+
y2
+
z,
следовательно,
 =
= .
.
Так
как вектор
 можно свободно перемещать в пространстве,
то длина произвольного вектора
можно свободно перемещать в пространстве,
то длина произвольного вектора =
= .
.

По
правилу сложения вектора
 =
= ‒
‒ ,
,
 =
(x2
‒
x1;
y2
‒
y1;
z2
‒
z1)
=
(x2
‒
x1;
y2
‒
y1;
z2
‒
z1)
Подставив
координаты
 в формулу длины вектора, получим формулу
для нахождения расстояния между точками:
в формулу длины вектора, получим формулу
для нахождения расстояния между точками:

‒ формула расстояния между точками.
Из
формулы
 =
= cos
α найдем
cos
α найдем
Cos
α =

Или

если
 =
(
=
( = (
= ( ).
).

Векторное произведение векторов (геометрический смысл, свойства).
Векторы
 ,
,
 и
и
 ,
взятые в указанном порядке, образуют
правую тройку векторов (рис. 2), если
,
взятые в указанном порядке, образуют
правую тройку векторов (рис. 2), если находится по ту сторону плоскости,
содержащей векторы
находится по ту сторону плоскости,
содержащей векторы и
и
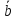 ,
откуда кратчайший поворот от вектора
,
откуда кратчайший поворот от вектора к
к можно совершить против часовой стрелки.
можно совершить против часовой стрелки.

В противном случае векторы образуют левую тройку векторов (рис. 1).
Векторным
произведением векторов
 и
и
 называется вектор
называется вектор =
=
 ×
× ,
удовлетворяющей следующим 3‒м свойствам:
,
удовлетворяющей следующим 3‒м свойствам:
│
 │=
│
│=
│ │·│
│·│ │·sin,
где
= (
│·sin,
где
= (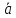 ;
; ).
). ⊥
⊥ ;
;
 ⊥
⊥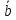 ;
;Векторы
 ,
,
 и
и ,
взятые в указанном порядке, образуют
правую тройку векторов.
,
взятые в указанном порядке, образуют
правую тройку векторов.
Геометрический смысл.

Sпароаллелограмма
= │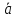 │·│
│·│ │·sin
=> │
│·sin
=> │ │
=│
│
=│ ×
× │,
│,
т.е.
│ ×
× │=Sпароаллелограмма
│=Sпароаллелограмма
Модуль
векторного произведения векторов
 и
и
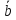 равенSпараллелограмма,
построенного на векторах ‒ множителях.
равенSпараллелограмма,
построенного на векторах ‒ множителях.


