Комплексные числа. Алгебраическая форма комплексного числа.
Задача
решения уравнений вида
,
послужила одним из поводов для расширения
понятия числа.
Рассмотрим уравнение:
,
Обозначим
– мнимая единица
,
тогда
Добавив ко всем действительным числам числа мнимые, получим множество комплексных чисел K.
Определение.
Числа
вида
(где
–действительная
часть;
–мнимая
часть;
– мнимая единица), называютсякомплексными.
Запись
называется алгебраической формой
комплексного числа.
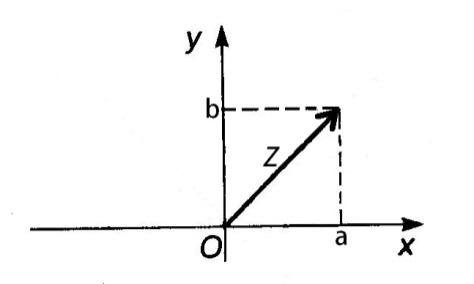
Геометрическое изображение
Ось OX – действительная ось
Ось OY – мнимая ось
Комплексная плоскость
RealZ = a– действительная часть
ImaginaryZ = b– мнимая часть
Действия над комплексными числами в алгебраической форме.
1) Сумма (разность) комплексных чисел
;
2) Произведение комплексных чисел
(учли,
что
)
3) Деление комплексных чисел
Для того чтобы выполнить деление комплексных чисел, надо числитель и знаменатель умножить на комплексное число, сопряженное знаменателю:
Следовательно,
Пример:
Тригонометрическая форма записи комплексных чисел.
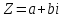
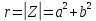–модуль
комплексного числа
,
следовательно
– тригонометрическая форма комплексного числа.
Пример:
;
a = 1;
b = – 1;
φϵIVчетверти.
Тогда
.
Действия над комплексными числами в тригонометрической форме.
Пусть даны два комплексных числа:
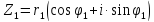
Тогда получим:
.
Примеры:
а) Пусть
z₁ = 3 ∙ (cos 20° + isin 20°);
z₂ = 2 ∙ (cos 35° + i sin 35°),
тогда
z₁· z₂ = 6 ∙ (cos 55° + i sin 55°).
б) Перемножить три комплексных числа:
2∙(cos 150° + i sin 150°), 3∙[cos (‒160°) + i sin (‒160°)] и 0,5∙(cos 10° + i sin 10°).
Решение: Модуль произведения 2 · 3 · 0,5 = 3.
Аргумент произведения 150° ‒ 160° + 10° = 0°.
Произведение равно 3 ∙ (cos 0° + i sin 0°).
Показательная форма записи комплексных чисел.
Воспользуемся тождеством Эйлера:
,
(
)
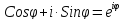Умножим
обе части этого равенства на
:
.
Следовательно,
– показательная форма комплексного числа.
Действия над комплексными числами в показательной форме.
Пусть даны два комплексных числа:
;
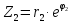
Тогда получим:
.
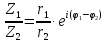
Пример:найти:
,
при k=
0; 1.
.
φϵIIчетверти.
Тогда
,
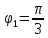При k= 0:
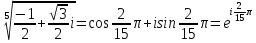
При k= 1:
