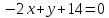Уравнения прямой (различные виды). Параметрические уравнения прямой.

Направляющим вектором прямой называется любой вектор параллельный данной прямой.

Пусть на прямой дана точка с координатами (,) и дан направляющий вектор прямой= (,).

Пусть точка М (x, y) – произвольная точка прямой, тогда вектор коллинеарен вектору.

По признаку коллинеарности эти векторы пропорциональны.

Обозначим коэффициент пропорциональности tи назовем параметром.

Тогда получим =t· .

Запишем это равенство в координатной форме:

() =t (,).

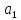Следовательно,

(1)

– параметрические уравнения прямой на плоскости.

По аналогии, в пространстве получим:

Уравнение прямой проходящей через две данные точки.

Из параметрических уравнений прямой выразим параметрt.

Получим:

– уравнение прямой проходящей через данную точку с данным направляющим вектором (каноническое уравнение).

В пространстве уравнение (2) примет вид:

Пусть на прямой даны две точки (,) и(,).

Тогда

= = (‒;‒).

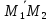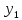Подставим его координаты в формулу (2).

Получим:

– уравнение прямой, проходящей через две данные точки.

В пространстве это уравнение примет вид:

Угловой коэффициент прямой. Уравнение прямой, проходящей через данную точку с данным угловым коэффициентом.

Угловым коэффициентом прямой называется тангенс угла наклона прямой, образованный ею с положительным направлением оси OX.

k= α, a≠ 90⁰

Пусть на прямой даны две точки М₁(х_1, y₁), M₂ (х_2, y₂).

Найдем угловой коэффициент этой прямой. Из ∆М₁M₂С получим

т.е.

– формула углового коэффициента прямой по координатам.

Заменим точку М₂(x, y) на произвольную точку M(x, y) и подставим ее координаты в формулу (1).

Получим:

Из формулы (2) следует

y ‒ y₁= k × (x ‒ x₁)

– уравнение прямой проходящей через данную точку с данным угловым коэффициентом.

Уравнение прямой, проходящей через данную точку с данным нормальным вектором (нормалью).

Нормальным вектором прямой(нормалью) называется любой вектор перпендикулярный данной прямой.

Обозначается = (a, b).

Пусть на прямой дана точка М₁ (x_1,y₁) и дан нормальный вектор прямой = (a, b).

Пусть М (x_, y) произвольная точка прямой.

Тогда вектор перпендикулярен вектору. Следовательно, их скалярное произведение×= 0.

Запишем это равенство в координатной форме.

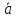Так как =(а; b) и = (x –x₁; y –y₁), то равенство ×= 0, согласно формуле, × = x₁× x₂+ y₁× y₂, в координатной форме примет вид:

a· ( x–x₁) + b· (y–y₁) = 0

– уравнение прямой, проходящей через данную точку с данным нормальным вектором.

Общее уравнение прямой.

Раскроем скобки в уравнении a·(x‒x₁)+ b·(y‒y₁)=0.

Следовательно, ax ‒ ax₁+ by ‒ by₁ = 0 или ax + by +(‒ ax₁‒ by₁) = 0.

Обозначим ‒ ax₁ - by₁=с,

тогда получим общее уравнение прямой:

ax + by + с = 0

– общее уравнение прямой.

Выразим из общего уравнения прямойyчерез x:

Следовательно,

‒ формула углового коэффициента по координатам нормального вектора.

Формула угла между прямыми.

Угол между прямыми: ; равен углу между их нормальными векторами, т. е.

() =().

Воспользовавшись формулой скалярного произведения векторов, получим:

Тогда

Если прямые заданные уравнениями:

; ,

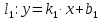тогда

Следовательно,

По формулам (1) или (2) находят угол между прямыми.

Условия параллельности и перпендикулярности прямых.

Если , то = 0. Следовательно,  = 0 и =0.

Получим:

‒ условие параллельности прямых.

Если , то  = и ‒ не существует, то есть 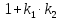= 0. Следовательно,

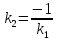
‒ условие перпендикулярности прямых.

Пример:

Даны уравнения сторон треугольника

,

,

.

Найти:

1) Длину │CD│ и уравнение высоты CD.

2) Систему неравенств определяющих треугольник.

3) B.

Решение:

Найдем координаты вершин треугольника.

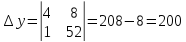
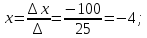
A (– 4; 8)

.

B (5; – 4)

C (10; 6)

1) Найдем уравнение высоты CD.

CD AB

;

.

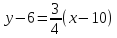│· 4

–уравнение высоты CD.

D (2; 0)

Найдем длину │CD│.

2) Найдем систему неравенств определяющих треугольник.

,

,

.

или – уравнениеAB.

–уравнение BC.

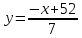или – уравнениеAC.

–система неравенств определяющих ∆ABC.

3) Найдем B.

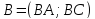
или