
- •V1: статистика
- •V2: общая теория статистики
- •V3: предмет, задачи. Основные категории и понятия теории статистики
- •V3: статистическое наблюдение
- •V3: сводка и группировка статистических данных
- •V3: абсолютные и относительные величины
- •V3: средние величины в статистике
- •V3:показатели вариации
- •V3:ряды распределения
- •V3: выборочное наблюдение
- •V3: статистическое изучение взаимосвязи социально-экономических явлений
- •V3: ряды динамики и их применение в анализе социально-экономических явлений
- •V3: индексный метод анализа
- •V2: социально-экономическая статистика
- •V3: статистика численности и состава населения. Статистика естественного движения и миграции населения
- •V3: статистика рынка труда, производительности и оплаты труда, затрат на рабочую силу
- •V3: статистика национального богатства
- •V3: макроэкономические показатели производства товаров и услуг в системе национальных счетов
- •V3: статистика рынка товаров и услуг
- •V3: статистика издержек производства и обращения, результатов финансовой деятельности предприятий
- •V3: статистика уровня жизни населения и отраслей социальной сферы
- •V3: статистика финансов предприятий и организаций
- •V3: статистика денежного обращения
V3: средние величины в статистике
I:
S: Средняя арифметическая используется, когда
+: расчет осуществляется по сгруппированным данным
+: расчет осуществляется по не сгруппированным данным
-: неизвестен знаменатель исходного соотношения
-: рассчитывают среднее квадратическое отклонение
-: рассчитывают средний темп роста
I:
S: Если все варианты признака уменьшить в А раз, то средняя арифметическая
+: уменьшится в А раз
-: уменьшится в А2раз
-: увеличится в А раз
-: увеличится в А2раз
-: не изменится
I:
S: Данная формула называется средней гармонической простой
+:
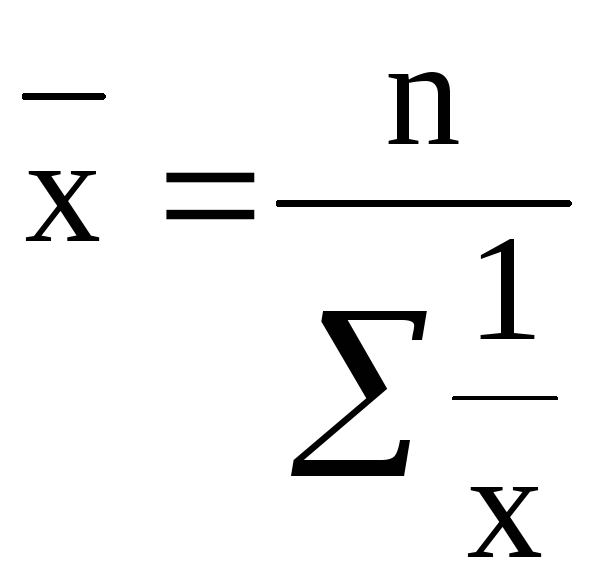
-:
![]()
-:

-:
![]()
-:
![]()
I:
S: Средней величиной называется
-: показатель, выражающий величину во времени
-: отношение одноименных показателей
+: уровень явления в расчете на единицу совокупности
-: численность единиц совокупности
I:
S: сумма отклонений индивидуальных значений признака от средней арифметической равна
+: 0
-: 1
-:-1
-: не имеет постоянного значения
I:
S: Формула средней квадратической используется для расчета
-: среднего темпа роста
-: среднего уровня в моментных рядах динамики
+: дисперсии
-: медианы интервального ряда
-: среднего линейного отклонения
I:
S: если все варианты признака уменьшить в 1,5 раза, а все веса в 1,5 раза увеличить, то средняя
+: уменьшится в 1,5 раза
-: уменьшится в 2,25 раза
-: увеличится в 2,25 раза
-: увеличится в 1,5 раза
-: не изменится
I:
S: Средняя арифметическая взвешенная совпадает со средней арифметической простой, если веса
-: подчиняются закону арифметической прогрессии
-: подчиняются закону геометрической прогрессии
+: равны между собой
-: выражены в промилях
-: выражены в процентах
I:
S: Соответствие между средними и их формулами
L1: средняя арифметическая взвешенная
L2: средняя геометрическая простая
L3: средняя квадратическая простая
L4: средняя гармоническая взвешенная
L5:
R1:
![]()
R2:
![]()
R3:
![]()
R4:

R5:

I:
S: Данная формула называется средней хронологической
+:

-:
![]()
-:

-:
![]()
-:
![]()
I:S: Для расчета среднего уровня в моментных рядах динамики применяется
-: средняя арифметическая
-: средняя гармоническая
-:средняя квадратическая
+: средняя хронологическая
-: средняя геометрическая
V3:показатели вариации
I:
S: Вариация зависимого признака, образовавшаяся под действием всех без исключения влияющих на него факторов, называется
-: систематической
-: случайной
-:особенной
+: общей
I:
S: Вариация – это изменение
-: явлений во времени
-: структуры статистической совокупности в пространстве
+: значений признака во времени и в пространстве
-: состава совокупности
I:
S: Коэффициент вариации характеризует
-: диапазон вариации признака
-: степень вариации признака
-: тесноту связи между признаками
+: пределы колеблемости признака
I:
S: Если все значения признака увеличить в А раз, то дисперсия
-: увеличится в А раз
+: увеличится в А2раз
-: уменьшится в А раз
-: не изменится
-: предсказать изменение нельзя
I:
S: Дисперсия постоянной величины равна
-: 1
+: 0
-: этой величине
-: предсказать величину невозможно
I:
S: Если все значения признака уменьшить на число С, то дисперсия
-: увеличится на С
-: уменьшится на С
+: не изменится
-: уменьшится на С2
-: увеличится на С2
I:
S: Разность между вариантой и средней показывает
-: коэффициент вариации
+: среднее линейное отклонение
-: дисперсия
-: размах вариации
-: среднее квадратическое отклонение
I:
S: Среднее квадратическое отклонение принято обозначать
-: L
-: σ2
+: σ
-: R
-: V
I:
S: Коэффициент вариации изменяется в границах
-: от 0 до 100 %
-: от 0 до 200 %
-: от 100 до 200 %
+: нижняя граница 0%, верхняя отсутствует
I:
S: Если изучаемая совокупность неоднородна по изучаемому признаку, значит коэффициент вариации
-: меньше 33,3 %
+: больше 33,3%
-: больше 0%
-: больше 100%
I:
S: Соответствие между показателями и их условными обозначениями
L1: коэффициент вариации
L2: размах вариации
L3: дисперсия
L4: среднее линейное отклонение
L5:
R1: V
R2: R
R3: σ2
R4: L
R5:X
