1. Шифрование письма в России.

25. Первый известный шифр в России “тарабарская грамота”. Это простая замена только согласных букв. Гласные не заменяются.

Б В Г Д Ж З К Л М Н

Щ Ш Ч Ц Х Ф Т С Р П

Такую таблицу замены называют парной, так как при шифровании буквы расположенные на одной вертикали переходят одна в другую. Сообщение ВЕЗУ ШАПКИ выглядит так: ШЕФУ ВАНТИ.

26. Петр Iупотреблял шифр простой замены ”цифирная азбука”, в которой буквы сообщения заменялись шифрообозначениями, являлись буквы, слоги, слова, а также и другие знаки – «пустышки», не соответствующие никаким знакам открытого текста.

27. Во второй половине 17 века придумали шифр простой замены “уголки”.

Рисунок 2.7

1. Шифры подполья России

28. “Тюремная азбука” для общения заключенных в соседние камеры перестукиванием – аналог квадрата Полибия 6х5. Буква передается парой номеров строки и столбца количеством стуков с короткой паузой между номерами с более длинной паузой между буквами К Т О и т.д.

	1	2	3	4	5
1	а	б	в	г	д
2	е	ж	з	и	к
3	л	м	н	о	п
4	р	с	т	у	ф
5	х	ц	ч	ш	щ
6	ь	ы	э	ю	я

А сначала лидером выстукивается азбука.

29. Парный шифр. Ключ – фраза, содержащая не менее 15 букв (половина алфавита без ё, й, ъ). Эти буквы ключевой фразы назовем информационными. Под ними подписываем оставшиеся буквы алфавита в порядке их следования в нем. Получаем таблицу простой замены, которую легко создаст/восстановит, помня ключевую фразу.

у

к

р

и

в

о

й

Н

а

т

а

л

ь

и в

с

е

л

ю

д

и канальи

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

б

г

ж

з

м

п

Ф

х

ц

ч

ш

щ

ы

э

я

Нумеруем по порядку 15 разных букв и подписываем оставшиеся буквы алфавита.

Получаем парную таблицу замены.

Для удобства пользования эту парную таблицу перепишем как полный алфавит.

А Б В Г Д Е Ж З И К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Э Ю Я

Х У М И Я Ы Р И З Г Ч В Ф П О Ж Щ Ц Б Н А Т Л Ь С Ш Е Ю Э Д

Явка провалена — сообщение

ДМГХОЖПМХЧЫФХ – шифровка ДМГХ ОЖПМ ХЧМФ Х

30. Аналог шифра “по книге” – шифр “по стихотворению”. Корреспонденты заучивают наизусть достаточно длинные стихотворения, такое, чтобы в нем встретились все буквы алфавита. Каждая буква сообщения шифруется парой чисел – номером строки, где встречается эта буква и номером буквы в ней. Для удобства работы стихотворение записывают на лист в клеточку в виде таблицы и нумеруют строки и столбцы записи. По окончании шифрования/расшифровывания запись таблицы уничтожают.

Шифровка имеет вид последовательности пар чисел.

3. Модулярная арифметика (mod-арифметика)

   1. Свойства целочисленных операций с modN

Любые целые числа сравниваются по модулю Nотображением их на множество модуляNравное {0, 1, 2,….N– 1} (1)

Для неотрицательных чисел а 0 отображение их на множество модуля получается циклическим вычитанием из ‘a’ величиныNдо тех пор пока не получится результатr, принадлежащий множеству модуля. Этот результат и есть число ‘a’ представленное (взятое) по модулюN

r=amodN(2)

Если a<N, тоr=a. Произошло отображение ‘a’ на самое себя.

Для отрицательных целых чисел a< 0 отображение на множество модуля распространяется путем циклического прибавленияNк а.

Операции сравнения по модулю Nнаглядно можно представить на оси целых чисел, см. рисунок ниже, как счет пачками поNединиц направленный от заданного числа в сторону множества модуляN.

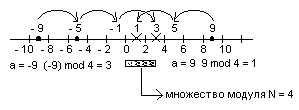
Рисунок 3.8

Легко видеть, что для неотрицательных чисел величина rесть остаток от целочисленного делителя ‘a’ наN.

В языке Pascalесть операцияmod– целый остаток от деления двух целых положи тельных чисел.

Понятия amod(-N) не существует, а взять отрицательное целое по модулюNможно так:

(-9)mod4 = - (9mod4) + 4 =-1 + 4 = 3 (3)

Можно и воспользоваться функцией Int(x) – целое число

Для а > 0 r = a mod N = a – N * Int(a/N) (4)

Для a < 0 r = a mod N = a + N * (Int(a/N)+1)

Например:

r = 9 mod 4 = 9 – 4 * Int(9/4) = 9 – 4*2 = 9 – 8 = 1

r = –9 mod 4 = –9 + 4 * (Int(+9/4) = - 9 + 4*(2+1) = 3

В теории чисел определено отношение() сравнимости целых чисел:

ab(modN) (5)

‘a’ сравнимо с ‘b‘ по модулюN, ‘a‘ и ‘b‘ – целые,N0, если только выполняется равенствоa=b+k*N

Еще говорят: Nделит (a–b):N| (a-b) и ‘b’ называютвычетомчисла ‘a' по модулюN.

Выражение (5) равносильно утверждению, что остатки от делений ‘a‘ и ‘b’ наNравны

17 5 (mod12)

означает, что

17 mod12 = 5

5 mod12 = 5

Для N= 12 полный набор вычетов есть {0, 1, 2, … 11}

Выражение a1 (modN) определяет все целые положительные ‘a’, остатки от деления которых наNравны 1.