2. Пример практической реализации простого цифрового скремблирования/дескремблирования сигнала речи

Н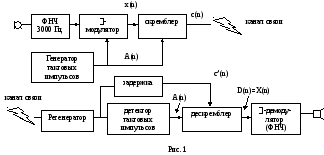а рис. 1 показана структурная схема такого устройства.

• М – микрофон

• ФНЧ – фильтр нижних частот с верхней граничной частотой 3000 Гц

• -модулятор – простейшее устройство оцифровывания аналогового сигнала речи (представление его -кодом)

• x(n) – -код (дельта-код). n – порядковый номер тактового импульса.

• c(n) – скремблированный -код (шифр поступающий на линию связи).

• регенератор – устройство восстановления П-образной формы сигнала из бит шифра, искаженных линией связи.

• задержка – синхронизирует одновременность поступления на дескремблер бит принятого шифра c’(n) с восстановленными тактовыми импульсами A(n).

• D(n)=x(n) – на выходе дескремблера получаем исходный -код.

• -демодулятор – преобразует -код в аналоговый сигнал речи. Реализуется простым активным ФНЧ 2-го порядка.

О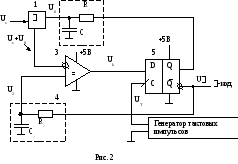дна из возможных простых принципиальных схем-модулятора приведена на рис. 2.

На рис. 3 показаны осциолограммы сигналов.

• 1 – аналоговый сумматор

• 2 – устройство усредняющее сигнал -кода (интегрирующая цепочка R₁C₁)

• 3 – компаратор

• 4 – -демодулятор (интегрирующая цепочка R₂C₂)

• 5 – D-триггер

• U_s – аналоговый сигнал речи

• U₀ – среднее значение амплитуды U_m импульсов -кода.

• U₂ – сигнал на выходе -демодулятора

• U_T – импульсы тактового генератора, записывающие положительные фронты состояние компаратора {‘0’,’1’}={0, 5 В} на выход Q D-триггера. ('0','1' – логические нуль и единица).

Когда U₂<(U_s+U₀), то U_k=’0’. На выход Q D-триггера записывается очередным положительным фронтом тактового импульса логический 0, а на ¯Q-логическая 1 (т. е. +5 В) и величина U₂увеличивается на один шаг U_2.

Так формируется сигнал -кодаU_, представляющий собой неструктурированный («сплошной») поток бит {0,1}, т. е. на разбитый на байты или слова.

3. Логическая операция xor как шифрование (дешифрование) потока бит.

Операция кодирования	Обратная операция декодирования
ci := xi XOR ci-1	yi := ci XOR ci-1

Пусть {x_i} – исходная последовательность потока бит.x{0,1}. {.} – символ множества.i– номер по порядку символаxв последовательности, {c_i} – кодированная (шифрованная, заксоренная) последовательность.

здесь x,c,y{0,1}

Реализация операций.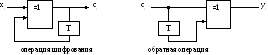

Здесь		– сумматор по модулю 2 c=aXORb.	a b c 0 0 0 0 1 1 1 0 1 1 1 0
		– задержка информации на один такт

Н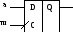апример, с помощью D-триггера. Значение «а» на входе D запоминается триггером на выходе Q в момент прихода на вход c положительного перепада тактовых импульсов. На рисунках схем реализации генератор тактовых импульсов не показан.

Покажем, что y_i = x_i

Обозначим суммирование по модулю 2 – 

Тогда c_i=x_ic_i-1(1)

y_i=c_ic_i-1(2)

Т. к.: y_i=c_ic_i-1=x_ic_i-1c_i-1, аc_i-1c_i-1= 0, тоy_i=x_i(3)

Или иначе (в общем случае):

т. к. c_i-1=x_i-1c_i-2, (4)

то, подставляя в (2) величины (1) и (4), получим:

y_i=x_i  c_i-1  x_i-1  c_i-2.

Но из (2) имеем

c_i-1c_i-2=y_i-1

Следовательно: y_i=x_ix_i-1y_i-1

Прямой подстановкой очередных значений xиyнетрудно убедиться, что выражения (5) и (3) эквивалентны.

Преобразование x_iy_iможно рассматривать как частный случай теории цифровых фильтров дляxиy– двоичных чисел и сумм по модулю два. Согласно теории цифровых фильтров возмем для выражений (1) и (2)Z-преобразование.

с(z)=x(z)c(z)z-1y(z)=c(z)z-1y(z)=c(z)(1z-1)

x(z)=c(z)c(z)z-1x(z)=c(z)(1z-1)

Т.к. операции сложения и вычитания по модулю 2 тождественны

и по правилу сдвига Z-преобразования получаем

y_i=x_i

Совместную пару операций XORкодирования/декодирования получим и при взятии дополнительной операции отрицания¯c_i

ci := xi XOR ci-1

xi := ci XOR ci-1

ci ¯ci 0 1 1 0

ci ¯ci

=1 T ci xi

=1 T ci xi

Т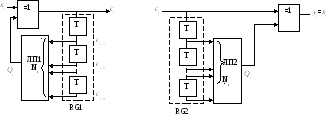еперь возьмем вместо одного элемента задержки несколько последовательно соединенных, т.е. регистр сдвига, а вместо одновходовой операции отрицания – логический преобразователь (ЛП), имеющий несколько входов и один выход

Снова получим совместную пару устройств кодирования/декодирования.

Такие устройства называют скремблерами/дескремблерами. ЛП удобно реализовать на микросхемах памяти (ПЗУ), содержащих 2ⁿячеек. ТогдаN_i– адресi-той ячейки.Q_i– информация (0, 1) записанная в ней.

Формула работы скремблера.

c_i=x_iQ_i

Q_i = φ(N)

N = c_i-1 + 2  c_i-2 + 2²  c_i-3 + … + 2^n-1c_i-n

N– десятичный эквивалент двоичного числаc_i-1c_i-2…c_i-n(c_i-1 – младший разряд) состояния регистра сдвигаRG1, являющегося адресом ячейки ПЗУ.

Итак, c_i=x_iφ(RG1)φ(N) =φ(RG1) (6)

Для дескремблера

y_i=c_iφ(RG1) (7)

Если функции для ЛП1 и ЛП2 одинаковы: φ(RG1) =φ(RG2), то выражения (6) и (7) аналогичны (1) и (2). Соответственно будем иметь и утверждение

y_i=x_i

Особенности свойств системы скремблер/дескремблер в общем случае с произвольной таблицей памяти ЛП не исследованы.

Получили широкое распространение и исследованы свойства системы скремблер/дескремблер с ЛП из линейки сумматоров по модулю два. Например:

T T T

T T T

З a b c = a XOR b десь для наглядности сумматор по модулю два обозначен