25.Сформулируйте теорему о достаточном условии оптимальности опорного решения.

Теорема (достаточное условие оптимальности опорного решения)

Если для опорного решения α⁰ канонической задачи линейного программирования на минимум (1) – (3) найдется базис, для которого все оценки неположительные, то есть δ_j≤0 для всех j = 1, 2, …, n, то вектор α⁰ является оптимальным решением данной задачи.

Доказательство

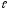Пусть δ₁, δ₂, …, δ_n – оценки системы векторов условий, приведенных к некоторому базису опорного решения α⁰. Если вектор β=(₁, …, _j, …, _n ) является произвольным допустимым решением канонической задачи линейного программирования (1) – (3), то по доказанной лемме имеем: f(β)=f(α) – δ_{j j}.

Так как, для любых j=1, 2, …, n по условию δ_j≤0 , а вектор β=(₁, …, _j, …, _n ) произвольное допустимое решение данной задачи, т.е. _j≥0 для всех j=1, 2, …, n , то f(β)≥f(α⁰). Следовательно, по определению вектор α⁰ является оптимальным решением задачи (1) – (3) на минимум

26.Сформулируйте теорему о неограниченности целевой функции кзлп.

Теорема ( о неограниченности целевой функции).

Пусть симплекс таблица приведена к некоторому базису опорного решения α канонической задачи линейного программирования (1) – (3) на минимум. Если при этом существует столбец А_s с положительной оценкой, т.е. δ_s > 0, где s=1, 2, …, n , а все остальные элементы этого столбца неположительные, т.е, α_is ≤ 0, i=1, 2, …, r , то целевая функция данной задачи неограниченна на множестве допустимых решений, и, следовательно, задача не имеет оптимального решения.

Доказательство

Пусть симплекс таблица приведена к базису А₁, А₂, …, А_r опорного решения α=(α₁, α₂, …, α_r, 0, 0, …, 0) и имеет вид:

A’1	A’2	…	A’r	A’r+1	…	A’s	…	A’n	B’
1	0	…	0	a/1,r+1	…	a'1s	…	a'1n	α1
0	1	…	0	a'2,r+1	…	a'2s	…	a'2n	α2
…	…	…	…	…	…			…	…
0	0	…	1	a'r,r+1	…	a'rs	…	a'rn	αr
0	0		0	δr+1	…	δs	…	δn	δ0

Следовательно, вектор ограничений В^’, а также вектор условий А’_s можно представить в виде линейной комбинации базисных векторов, а именно,

(12)А^’₁ α₁+ А^’₂ α₂ + …+ А^’_r α_r = В^’ и А^’₁ a^’_1s + А^’₂ a’_2s + … + А^’_r a’_rs = A^’_s

(13)А^’₁ a^’_1s + А^’₂ a’_2s + … + А^’_r a’_rs – A^’_s =Ө .

Помножив соотношение (13) на переменную t > 0 и вычтя его из соотношения (12), получим:

А^’₁ ( α₁ – t a^’_1s ) + А^’₂ ( α₂ – t a’_2s ) + … + А^’_r (α_r – t a’_rs) + A^’_s t = B’.

Из последнего соотношения и с учетом того, что a’_is ≤ 0, следует, что вектор

Α_t = (α₁ – t a^’_1s , α₂ – t a’_2s , …, α_r – t a’_rs , 0, …, 0, t, 0, …, 0 )

является допустимым решением задачи (1) – (3). По лемме о целевой функции для допустимого решения α_е имеем

f(α_t) = f(α) – δ₁ ( α₁ – t a^’_1s ) – δ₂ ( α₂ – t a’_2s ) – …– δ_r ( α_r – t a’_rs ) – δ_s t .

С учетом того, что оценки базисных векторов равны нулю, т.е., δ₁= δ₂= …= δ_r=0, значение целевой функции можно записать в виде: f(α_t) = f(α) – δ_s t. Так, как δ_s > 0 , то при t→ +целевая функция неограниченно уменьшается, т.е.,f(α_t) → –, и, следовательно, задача не имеет оптимального решения