Цель работы: знакомство с методами измерения частоты исследуе­мого сигнала; градуировка шкалы генератора стандартных сигналов (ГСС).

Основные понятия

В зависимости от диапазона измерений и требуемой точности ис­пользуют различные средства и методы измерений.

Для измерения частоты в узком диапазоне (45-55; 450-550 Гц и т.д.) при наибольшей частоте 2500 Гц применяют электродинамические и элек­тромагнитные частотомеры. Классы точности электродинамических часто­томеров 1; 1,5; электромагнитных частотомеров 1,5; 2,5.

Для измерения низкой частоты в узком диапазоне (48-52; 45-55 Гц и т.д.) могут применяться резонансные частотомеры. Класс точности таких частотомеров 1-2,5.

В диапазоне высоких и сверхвысоких частот частота может изме­ряться высокочастотными резонансными частотомерами, в которых ис­пользуется колебательный контур из катушки индуктивности и конденса­тора. Погрешность измерения частоты в этом случае составляет ±(0,05-0,1)%.

Для измерения частоты в широком диапазоне (от 10 Гц до несколь­ких мегагерц) могут применяться электронные частотомеры. Класс точно­сти 0,5-2,5.

Для измерения частоты электрических сигналов также применяется метод сравнения. Этот метод достаточно прост, обладает сравнительно вы­сокой точностью и пригодностью для использования в широком диапазоне частот. Измеряемая частота определяется по равенству или кратности из­вестной частоты. Индикатором равенства или кратности частот может служить электронный осциллограф. Измерения частоты можно произво­дить при линейной, синусоидальной и круговой развертках.

При линейной развертке период сигнала измеряемой частоты f_x сравнивается с периодом развертки либо с периодом меток времени калиб­ратора длительности Т_м. В первом случае учитывается коэффициент раз­вертки т, а результат измерения част оты f_x определяется по формуле

, где а - период сигнала частоты f_x, отсчитанный в делениях шкалы на экране осциллографа. При измерении частоты с помощью меток времени калибратора длительности устанавливают на экране несколько периодов измеряемой частоты, регулируют период меток Т_м так, чтобы их изображение попадало в одну и ту же точку каждого периода. В этом слу­чае измеряемая частота

где п - число меток, находящихся в пре­делах одного периода исследуемого напряжения. Преимуществом этих способов является возможность исследования колебания любой формы, недостатком - низкая точность; погрешность может достигать + (5-10)%.

Более точные результаты могут быть получены при сравнении двух колебаний синусоидальной формы методом фигур Лиссажу. На одну из пар отклоняющих пластин осциллографа подается синусоидальное напря­жение. Измеряя известную частоту, добиваются получения кривой на эк­ране в виде неподвижной или медленно перемещающейся фигуры Лисса­жу. По виду фигур Лиссажу судят о частоте и фазовом сдвиге исследуемо­го напряжения. Простейшей фигурой Лиссажу является эллипс, частными случаями которого является окружность и прямая. Условием появления эллипса является совпадение частот напряжений, подаваемых на верти­кально отклоняющие у и горизонтально отклоняющие х пластины.

Пусть

Соответственно отклонение луча по горизонтали и вертикали, при воз­действии на него напряжения U_x и U_y, будет определяться выражениями:

Из (1) получим

Из (2) имеем

Подставляя в (4) формулы (3) и (5), получим:

Формула (6) определяет траекторию движения луча для произволь­ных значений φ

При φ =0, у -уравнение прямой, проходящей через 1-й и 3-й квадранты.

При φ =π 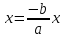уравнение прямой, проходящей через 2-й и 4-й квадранты.

При φ = выражение (6) принимает вид:

Возводя в квадрат, получим:

Или

- уравнение эллипса;

при а = b получается уравнение окружности:

у²+х²=а².

При неравных частотах и выполнении условия кратности где

n- целое число, фигуры Лиссажу будут иметь более сложную форму. Кратность частот при любой форме кривых легко определяется по числу касаний n_г и п_в осциллограммы горизонтальным и вертикальным прямым. Отношение частот определяется условием:

Примеры:

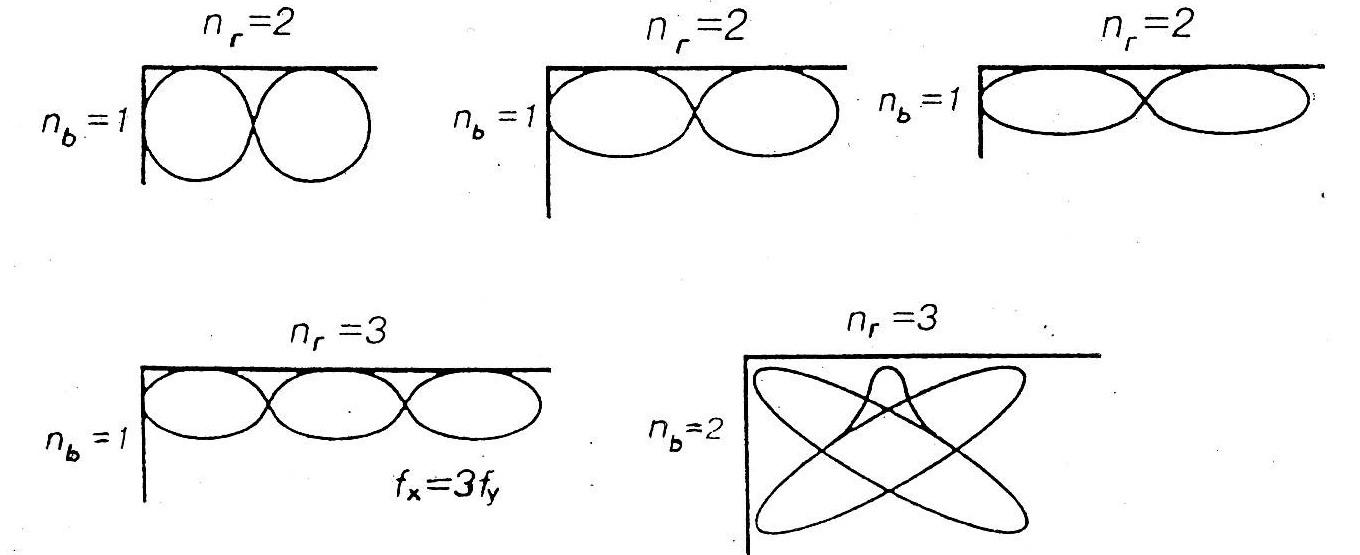
Определение частоты по фигурам Лиссажу достаточно трудоемко, поскольку неподвижность фигур достигается лишь при целочисленной кратности и достаточно высокой стабильности обеих частот. Чем выше не­стабильность, тем быстрее изменяются фигуры Лиссажу и тем труднее считать число касаний.

Значительно более точным является метод круговой развертки, когда напряжение образцовой частоты f_obpподается на R-C цепь, после чего, в виде двух напряжений со сдвигом фаз на 90°, поступает на Y и X входы и электронно-лучевой трубки осциллографа (рис.2).

Линия развертки в виде эллипса или окружности вращается со ско­ростью один оборот за период сигнала образцовой частоты. Напряжение неизвестной частоты подается на канал Z для модуляции электронного луча по яркости. Иссле дуемое напряжение неизвестной частоты формиру­ет короткие прямоугольные импульсы для подачи их в цепь модулятор -катод трубки. При совпадении образцовой частоты с частотой исследуемо­го напряжения такой импульс наблюдается в виде светящейся метки на эл­липтической развертке. При кратности частот f = nf_обр на эллиптической

диаграмме наблюдается п меток. При этом, если равенство выполняется точно, то светящиеся метки будут неподвижны, если

метки вра­щаются по развертке тем быстрее, чем больше

Важно добить­ся неподвижности меток. Измерения частоты данным методом осуществ­ляется с помощью приемника- компаратора ПК-50.