методические указания для лабораторных работ / Атомная физика и оптика / Кольца Ньютона

Цель работы: наблюдение интерференционной картины « Кольца Ньютона » в .отраженном свете; изучение явления интерференции в тонких слоях; определение радиуса кривизны линзы и длины волны интерферирую­щих лучей; определении разности хода интерферирующих волн и сравнение ее с длиной когерентности.

ОСНОВНЫЕ ПОНЯТИЯ

Физическим явлением, используемым для выполнения этой лабора­торной работы, является явление интерференции в тонких пленках. Явление интерференции заключается в наложении (суперпозиции) двух или более волн друг на друга, в результате которого получается устойчивая картина максимумов и минимумов интенсивности. Рассмотрим более подробно ин­терференцию в параллельных лучах, падающих под произвольным углом на плоскопараллельную прозрачную пластинку.

При падении волны на тонкую прозрачную пластинку или пленку происходит отраже­ние от обеих поверхностей. В результате возникают две световые волны, которые при определенном соотношении между толщи­ной пластинки Ь, показателем преломления среды π и длиной волны света λ -могут ин­терферировать, образуя светлые и темные полосы. Пусть на прозрачную плоскопарал­лельную пластинку с показателем преломления, равным п, падает плоская световая волна,

которую можно рассматривать как параллельный пучок лучей. Пластинка отбрасывает вверх два параллельных пучка света, из которых один образо­вался за счет отражения от верхней поверхности пластинки, второй - вслед­ствие преломления на верхней поверхности, прохождения внутрь пластинки и отражения от нижней поверхности. Кроме этих двух пучков, пластинка от­бросит вверх пучки, возникающие в результате трех-, пяти- и т.д. кратного отражения от поверхности пластинки. Однако ввиду их малой интенсивности мы эти пучки принимать во внимание не будем. Не будем также интересо­ваться пучками, прошедшими через пластинку.

Разность хода, приобретаемая лучами 1 и 2 до того, как они сойдут­ся в точке В, равна

(1)

где s₁ длина отрезка ВС, a s₂- суммарная длина отрезков АО и OB, n - пока­затель преломления пластинки. Показатель преломления среды, окружающей пластинку, полагаем равным единице. Из рисунка видно, что

При вычислении разности фаз А между колебаниями в лучах 1 и 2 нужно, кроме оптической разности хода , учесть возможность изменения фа­зы волны при отражении. В точке В отражение происходит от границы раз­дела среды, оптически менее плотной, со средой, оптически более плотной. Поэтому фаза волны претерпевает изменение на п. В точке О отражение про­исходит от границы раздела среды, оптически более плотной, со средой, опти­чески менее плотной, так что скачка фазы не происходит. В итоге между лу­чами 1 и 2 возникает дополнительная разность фаз, равная я. Ее можно учесть, добавив к 5 ( или вычтя из нее) половину длины волны в вакууме В результате получим

У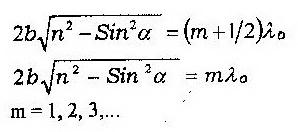казанное соотношение представляет условия максимума (2.1) и минимума (2.2) интенсивности, которые имеют вид:

Из соотношения (2.1) и (2.2) следует, что если освещать пластинку рассеянным светом, в котором представлены лучи всевозможных направле­ний, то интерференционная картина наблюдается только для тех из них, ко­торые падают под определенными углами а. Полученную интерференцион­ную картину называют полосами равного наклона, которые локализованы в бесконечности (рис.1).

Для того, чтобы интерференционная картина была устойчивой, не­обходимо, чтобы интерферирующие волны или лучи были когерентными. Когерентными называются волны одной и той же частоты, разность фаз ко­лебаний в которых остается постоянной во времени.

Когерентные световые волны можно получить, разделив (с помо­щью отражений или преломления) волну, излучаемую одним источником, на две части. Если заставить эти две волны пройти разные оптические пути, а потом наложить их друг на друга, наблюдается интерференция. Разность оп­тических длин путей, проходимых интерферирующими волнами, не должна быть очень большой, так как складывающиеся колебания должны принадле­жать одному и тому же результирующему цугу волн. Если эта разность будет порядка 1м, належатся колебания, соответствующие разным цугам, и раз­ность фаз между ними будет непрерывно меняться хаотическим образом. Это приведет к неустойчивости интерференционной картины, а следовательно, к невозможности ее наблюдения.

Различают временную и пространственную когерентность. Мы начнем с рассмотрения временной когерентности. Время t_mr, за которое слу­чайное изменение фаты волны cp(t) достигает значения порядка л, называется временем когерентности. За это время колебание как бы забывает свою пер­воначальную фазу и становится некогерентным по отношению к самому се­бе. Пространственная когерентность зависит также от величины долгшеров-ского уширения спектральной линии ???, которое возникает за счет хаотиче­ского движения излучающих молекул.

Расстояние /'„„= с t ий-, на которое перемещается волна за время W, называется длиной когерентности ( или длиной цуга). Длина когерентности есть то расстояние, на котором случайное изменение фазы достигает значе­ния ~??. Для получения интерференционной картины' путем деления естест­венной волны на две части необходимо, чтобы оптическая разность хода Д была меньше, чем длина когерентности-Это требование ограничивает число видимых интерференционных полос.' С увеличением номера полосы m раз­ность хода растет, вследствие чего четкость полос делается все хуже и хуже. Если толишна пленки изменяется («клин») и освещается параллельным пуч­ком света ( а = const), то интерференционная картина наблюдается при от­ражении от тех поверхностей, для которых b = const - это полосы равной тол­щины. В обоих случаях интерференция наблюдается только для той части отраженных волн, для которых толщина пластинки удовлетворяет условию Ъ <.Х² / (2ДД,), то есть сравнима с длиной когерентности , где &1* интервал длин волн в пределах падающего пучка света, - величина -10^-5 нм.

Классическим примером полос равной толщины являются кольца Ньютона. Они наблюдаются при отражении света от соприкасающихся друг с другом плоскопараллельной толстой стеклянной пластинки и ллосковы-пуклой линзы с большим радиусом кривизны. Роль тонкой пленки играет воздушный зазор между пластинкой и линзой; При отражении от других по­верхностей интерференционная картина не наблюдается, так как для них не выполняется условие когерентности. При нормальном падении света полосы равной толщины в этом случае, имеют вид концентрических окружностей, поскольку одинаковую оптическую разность хода имеют лучи, прошедшие одну и ту же толщину зазора по окружности радиуса г (см. далее рис.5). Ра­диусы темных колец определяются да формулы (2.2) при n = 1, а=0 . Так как из (2.2)

При малой величине b

Следовательно

Таким образом, интерференционная кар­тина представляет концентрические че­редующиеся темные и светлые кольца, в центре ее наблюдается темное пятно. Минимум интенсивности в этой точке обусловлен изменением фазы волн на П при отражении от пластинки. На рис.2 показана интерференционная картина колец Ньютона, наблюдающаяся при правильно отрегулированном изображе­нии в микроскопе в монохроматическом свете. Визирная линия при этом уста­новлена на второе светлое кольцо.

МЕТОДИКА ЭКСПЕРИМЕНТА Описание лабораторной установки

Лабораторная установка схематически изображена на рис.3. Она со­стоит из измерительного микроскопа 1 с устройством освещения 2, блока питания осветителя 3, устройства перемещения оптической системы «КольцаНьютона» 4 с микрометрическим винтом 5. Окуляр микроскопа 6 имеет ви­зирную линию, которую при измерениях устанавливают касательно к изо­бражению нужного кольца. Осветительное устройство допускает возмож­ность наблюдения колец в трех различных участках спектра, для чего служит передвигающаяся кассета 7 с тремя светофильтрами - красным, зеленым и синим. На столике микроскопа укреплена оптическая система, состоящая из плоскопараллельной стеклянной пластинки и соприкасающейся с ней плос­ковыпуклой линзой.

Кольца Ньютона наблюдаются в отраженном свете, для чего ис­пользуется оптическая система, изображенная на рис. 4.

Для измерения радиусов колец Ньютона линза Л и пластинка П помещены на столике изме­рительного микроскопа и пе­ремещаются относительно его оси микрометрическим вин­том. Свет от лампы S через фокусирующую линзу и смен­ные светофильтры С, поме­щенные в кассету, направля­ются на стеклянную плоскопараллельную поворотную пла­стинку 1ТП, установленную под утлом 45 к оси микроскопа и, отразившись от нее, попада­ет на линзу Л, которая касается пластинки П.

Интерференционная картина наблюдается в увеличенном виде через окуляр

микроскопа О.

Порядок выполнения работы

1.Включить лампу, выбрать один из цветных светофильтров - крас­ный, зеленый или синий - но заданию преподавателя, и с помощью измерительного винта настроить установку так, чтобы нить в поле зрения микроскопа пересекала кольца.

2.Определить положение центра ин­терференционной картины Хо (рис. 5 ), для чего совместить нить мик­роскопа с касательной к m темному кольцу в диаметрально противопо­ложных точках X' и X*. Измерение провести для нескольких колец. Что­бы люфт измерительного винта не сказывался на результатах измере­ний, их нужно проводить при враще­нии барабана микрометра в одну сторону.

3.Измерить несколько (3-5) раз расстояние от центра интерференци­онной карими до одного из темных колец с произвольным номером m=3÷5, для чего водаестить нить с касательной к кольцу справа и отсчитать величи­ну Х_m.

4.Измерить 3-5 раз расстояние от центра интерференционной картины до одного из темных колец с номером т', меньшим чем m, отсчитав величи­ну Х_m'.

5.Повторить измерения пунктов 3,4 для других светофильтров.

ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЯ

1. Рассчитать координату Х₀ центра интерференционной картины по формуле:

2. Вычислить средние радиусы темных колец Ньютона порядков m и m’

для различных светофильтров:

3. По известной длине волны максимума пропускания какого-либо све­тофильтра Хо определить радиус кривизны линзы, используя формулу

4. По найденному радиусу кривизны линзы определить длину волны максимума пропускания других светофильтров, используя данные ра­диусов темных колец для соответствующих светофильтров и формулу:

5. Вычислить толщину воздушного зазора в том месте, где наблюдается темное кольцо номера m, по формуле (5)

6. Проверить соотношение (4), используя измеренные значения R,b и т. п.

(13)

7. Оценить длину когерентности по формуле:

где ∆λ - доплеровское уширение спектральной линии, ∆λ ~10^-3 пм.

(14)

8. Вычислить оптическую разность хода лучей по формуле:

и сравнить ее с длиной когерентности.

Порядок расчета погрешностей

1. Погрешность определения положения центра интерференционной картины и радиуса колец рассчитать по методике оценки погреш­ностей прямых измерений. Наиболее вероятное значение измеряемой величины находится по формуле среднего арифметического значения нескольких последова­тельных измерений этой величины

где n -число измерений. После этою вычисляется среднеквадратическое отклонение измеряемой величины от среднего по формуле:

Вычислил величины х и S(x ), необходимо по таблице распределе­ния Стьюдента определить коэффициент Стьюдента I, зависящий от значения выбранной доверительной вероятности Р и количества из­мерений. Из таблицы распределения Стьюдента видно, что эти пара­метры взаимозависимы, поэтому не рекомендуется при малом числе измерений выбирать высокое значение доверительной вероятности. После этого можно определить значение абсолютной погрешности ре­зультата измерений по формуле:

при доверительной вероятности Р

2. Погрешности. R, Х₀ и Ь найти по методике расчета погрешностей косвенных измерений.

По упрошенной методике расчета для этого необходимо из ра­бочей формулы для соответствующей величины составить формулу

для расчета погрешности. Например, для расчета погрешности изме­рения величины λ₀формулу ( 11 ) записываем в виде функции тех переменных, которые имеют свои погрешности

После этого записываем формулу погрешности для λ'₀ в виде:

В этих формулах в подкоренных выражениях стоят квадраты частных дифференциалов функции (17) но всем ее переменным, а коэффици­ент k определяется согласно указаниям [4]. Преобразуя подкоренное выражение в (18) с учетом формулы (17) и считая, что первое и второе слагаемые подкоренного выражения можно принять равными друг другу, получим:

По этой формуле следует вычислять абсолютную погрешность измерения величины λ'₀,

Получите самостоятельно аналогичные формулы для вычисления погреш­ностей величин R и Ь, исходя из формул (10) и (12 ).

Вопросы для самопроверки

1.Что называется явлением интерференции? Какие условия должны быть соблюдены для наблюдения этого явления?

2 Каковы условия возникновения максимумов и минимумов при интерференции двух волн?

3 Что такое геометрическая и оптическая разности хода волн от двух источников?

4.Опишите оптическую систему, которая используется при наблюдении

интерференционной картины « Кольца Ньютона ».

5.Что такое длина когерентности? На какие виды подразделяется понятие когерентности?

6.Объясните, почему в отраженном свете в центре интерференционной картины « Кольца Ньютона » наблюдается темное пятно?

7.Почему в формулу (14) для оптической разности хода лучей в кольцах Ньютона не входит показатель преломления n?

8.В чем заключается физическая причина допплеровского уширения спек­тральных линий? Пояснить физический механизм уширения.

Литература

1. Савельев И.В. Курс физики.Т.2. М.'.Наука, 1982. 496 с.

2. Яворский Б.М.,Детлаф А.А. Справочник по физике. М.:Наука, 1985. 512 с.

3. Лабораторные занятия по физике/Под ред . Л.Л. Гольдана. М.'.Наука, 1983.704 с.

4. Терешин Ю.В. Обработка результатов измерений: Метод, указания. Сара­тов, 1983.

Время, отведенное на лабораторную работу