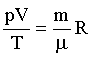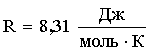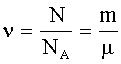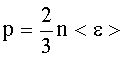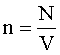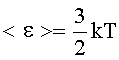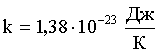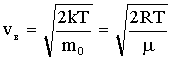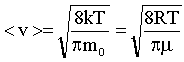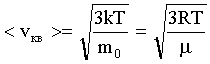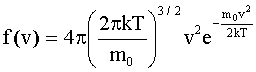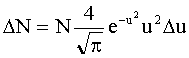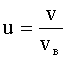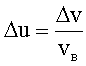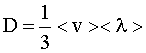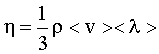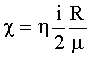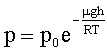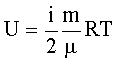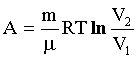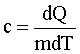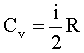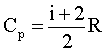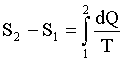1.5. Статистическая физика и термодинамика.

1.5.1. Пояснение к рабочей программе

При изучении основ статистической физики и термодинамики следует уяснить следующее. Существует два способа описания процессов, происходящих в макроскопических телах (т.е. телах, состоящих из очень большого числа частиц - атомов или молекул), - статистический и термодинамический.

Статистическая (молекулярная) физика пользуется вероятностными методами и истолковывает свойства тел, непосредственно наблюдаемых на опыте (такие, как давление и температура), как суммарный, усредненный результат действия отдельных молекул. Молекулярно-кинетическая теория позволяет раскрыть глубинный смысл экспериментальных закономерностей, например, таких как уравнение Менделеева-Клапейрона. При решении задач на эту тему основное внимание уделено таким вопросам программы, как уравнение Менделеева-Клапейрона, закон Дальтона для смеси газов (в контрольной работе это задачи 501-510), уравнение молекулярно- кинетической теории (в контрольной работе это задачи 511-520).

Следует обратить внимание на статистические законы. Распределение молекул идеального газа по скоростям описывает распределение Максвелла, а по потенциальным энергиям - распределение Больцмана. Зависимость давления от высоты для изотермической атмосферы описывается барометрической формулой. Этим вопросам посвящены задачи 521-530 контрольной работы.

При изучении явлений переноса, к которым относятся теплопроводность, диффузия и внутреннее трение, следует уяснить, что эти явления сходны между собой. В основе этого сходства лежит одинаковый молекулярный механизм перемешивания молекул в процессе их хаотического движения и столкновений друг с другом. Изучение явлений переноса посвящены задачи 531-540.

Важно усвоить, что термодинамика, в отличие от молекулярной физики, не изучает конкретные взаимодействия, происходящие с отдельными атомами или молекулами, а рассматривает взаимопревращения и связь различных видов энергии, теплоты и работы.

При изучении основ термодинамики нужно четко усвоить такие понятия как термодинамическая система, термодинамический процесс, внутренняя энергия, энтропия и т.д. Задачи контрольной работы охватывают такие важные соотношения и понятия как первое начало термодинамики, внутренняя энергия, работа при различных изопроцессах (задачи 541-550).

Задачи 551-560 посвящены изучению второго начала термодинамики, которые формулируются как закон возрастания энтропии. Этот закон определяет направление протекания термодинамических процессов.

1.5.2. Основные формулы

Уравнение состояния идеального газа (уравнение Менделеева-Клапейрона) : где р - давление газа; V - его объем; Т - термодинамическая температура (по шкале Кельвина); R - газовая постоянная m - масса вещества; μ - молярная масса.
Количество вещества: где N - число молекул; NA - число Авогадро (число молекул в 1 моле вещества).
Закон Дальтона для смеси газов: где р - давление смеси газов; - давление n-го компонента смеси (парциальное давление); n - число компонентов смеси.
Основное уравнение молекулярно-кинетической теории газов: где n - концентрация молекул:
Средняя кинетическая энергия поступательного движения молекулы: где k - постоянная Больцмана: Т - термодинамическая температура.
Зависимость давления газа от концентрации и температуры:
Скорость молекул наиболее вероятная: где - масса одной молекулы ; средняя арифметическая: средняя квадратичная:
Распределение молекул газа по скоростям (распределение Максвелла): где е = 2,71... - основание натуральных логарифмов.
Приближенная формула вычисления числа молекул, скорости которых лежат в интервале v÷v+Δv, где Δv<<v: где N - полное число молекул.
Средняя длина свободного пробега молекулы: где d - эффективный диаметр молекулы.
Среднее число столкновений молекулы в единицу времени: где <v> - средняя арифметическая скорость молекулы.
Коэффициент диффузии:
Коэффициент вязкости (внутреннего трения): где ρ - плотность.
Коэффициент теплопроводности:
Барометрическая формула: где р - давление газа на высоте h; p0 - давление газа на высоте h = 0.
Внутренняя энергия идеального газа: где i - число степеней свободы (i = 3 - для одноатомного газа, i = 5 - для двухатомного газа, i = 6 - для трехатомного газа).
Работа расширения газа при процессе: изобарном (изобарическом) (p = const): изотермическом (T=const):
Первое начало термодинамики: где Q - количество теплоты, подводимое к системе; ΔU - изменение внутренней энергии; А - работа, совершаемая системой против внешних сил.
Удельная теплоемкость:
Молярная теплоемкость: молярная теплоемкость изохорная молярная теплоемкость изобарная
Изменение энтропии при переходе из состояния 1 в состояние 2: где dQ - элементарное тепло, Т - термодинамическая температура.