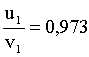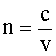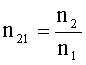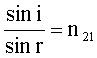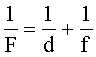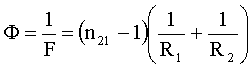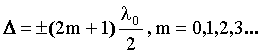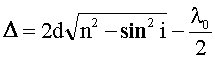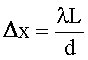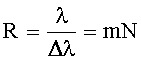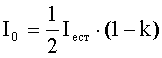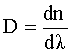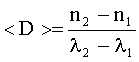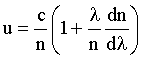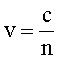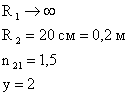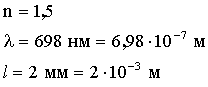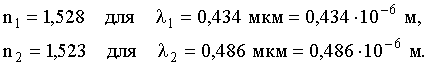1.4.2. Основные формулы
|
Абсолютный показатель преломления где с - скорость света в вакууме, с=3·108 м/с, v - скорость распространения света в среде. |
|
|
Относительный показатель преломления где n2 и n1 - абсолютные показатели преломления второй и первой среды. |
|
|
Закон преломления где i - угол падения, r - угол преломления. |
|
|
Формула тонкой линзы где F - фокусное расстояние линзы, d - расстояние от предмета до линзы, f - расстояние от линзы до изображения. |
|
|
Оптическая сила линзы где R1 и R2 - радиусы кривизны сферических поверхностей линзы. Для выпуклой поверхности R>0. Для вогнутой поверхности R<0. |
|
|
Оптическая длина пути: где n - показатель преломления среды; r - геометрическая длина пути световой волны. |
|
|
Оптическая
разность хода:
|
|
|
Условие интерференционного максимума: минимума: где λ0 - длина световой волны в вакууме; m - порядок интерференционного максимума или минимума. |
|
|
Оптическая разность хода в тонких пленках в отраженном свете: в проходящем свете: где d - толщина пленки; i - угол падения света; n - показатель преломления. |
|
|
Ширина интерференционных полос в опыте Юнга: где d - расстояние между когерентными источниками света; L - расстояние от источника до экрана. |
|
|
Условие главных максимумов дифракционной решетки: где d - постоянная дифракционной решетки; φ - угол дифракции. |
|
|
Разрешающая способность дифракционной решетки: где Δλ - минимальная разность длин волн двух спектральных линий, разрешаемых решеткой; m - порядок спектра; N - общее число щелей решетки. |
|
|
Закон Малюса: где I0 - интенсивность плоско-поляризованного света, падающего на анализатор; I - интенсивность света, прошедшего через анализатор; α - угол между плоскостью поляризации падающего света и главной плоскостью анализатора. |
|
|
Связь интенсивности естественного света Iест с интенсивностью света, прошедшего поляризатор (и падающего на анализатор): где k - относительная потеря интенсивности света в поляризаторе. |
|
|
Дисперсия вещества |
|
|
Средняя дисперсия |
|
|
Групповая скорость света |
|
|
Фазовая скорость света |
|
-
оптические пути двух световых волн.
1.4.3. Примеры решения задач по оптике
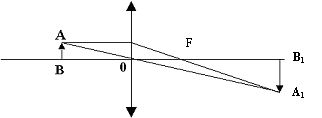
Задача 1. На каком расстоянии от предмета нужно поместить экран, чтобы плоско выпуклая линза с радиусом кривизны R = 20 см и показателем преломления n = 1,5 давала изображение предмета, увеличенное в 2 раза?
|
Дано: |
|
Рис.6 |
|
|
|
|
|
Найти: |
a |
|
Решение: Построим изображение предмета (рис. 6). Из чертежа следует, что ΔАОВ ˜ΔА1 ОВ1 . Из подобия следует:
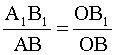
По
условию задачи увеличение
.
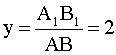Следовательно:
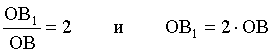(1)
Из принятых обозначений: ОВ = d, ОВ1 = f. Тогда: f = 2d. Определим оптическую силу линзы:
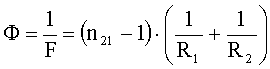(2)
Проведем вычисления:
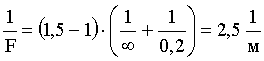
Воспользуемся формулой тонкой линзы:
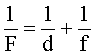(3)
Подставим (1) в (3):
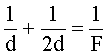
Тогда: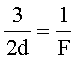 
Найдем
расстояние от предмета до линзы: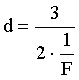 
Вычислим: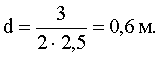 
Расстояние от предмета до экрана равно:
Ответ: а = 180 см.
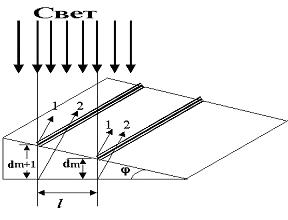
Задача 2. На стеклянный клин падает нормально монохроматический свет (λ = 698 нм). Определить угол между поверхностями клина, если расстояние между соседними интерференционными минимумами в отраженном свете равно 2 мм.
|
Дано: |
|
Рис.7 |
|
|
|
|
|
Найти: |
φ |
|
Решение: Параллельный пучок света, падая нормально к грани, отражается как от верхней (луч 1), так и от нижней (луч 2) грани клина (рис. 7). Лучи 1 и 2 когерентны между собой и интерферируют. Интерференционная картина представляет собой чередование темных и светлых полос. Темные полосы видны на тех участках клина, для которых оптическая разность хода кратна нечетному числу половины длины волны (условие минимума):
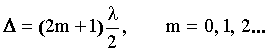
Оптическая разность хода в отраженном свете равна:
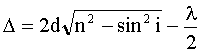
где i - угол падения луча. Так как по условию свет падает нормально, то i = 0 и sini = 0. Произвольной полосе с номером m соответствует толщина dm , а (m+1) полосе соответствует толщина клина dm+1 . Запишем условие минимума для двух соседних темных полос:
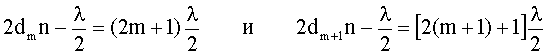
Отсюда:
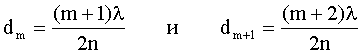
Тогда:
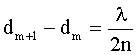
Из
рисунка: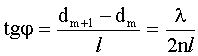 
Вычислим:
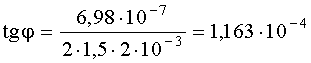
Тангенс
мал, поэтому: 
Ответ:
Задача 3. Измерение дисперсии показателя преломления оптического стекла дало n1 = 1,528 для λ1 = 0,434 мкм и n2 = 1,523 для λ2 = 0,486 мкм. Вычислить отношение групповой скорости к фазовой скорости для света с длиной волны 0,434 мкм.
|
Дано: |
|
|
|
|
|
Найти: |
|
Решение: Зависимость групповой скорости u от показателя преломления n и длины волны λ имеет вид:
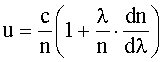(1)
где с - скорость света в вакууме.
Фазовая
скорость определяется как
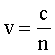(2)
Разделив выражение (1) на (2), получим:
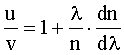
Средняя
дисперсия: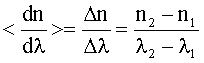 
Для длины волны λ1 и средней дисперсии имеем:
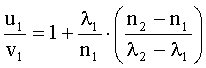
Вычисления:
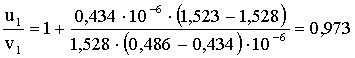
Ответ: 