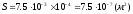Лабораторная работа №1.

Кафедра прикладной физики.

Изучение свойств ферромагнетиков

(Гистерезис).

Выполнил: ст. гр. ПВС-21

Проверил:

Саратов, 2001.

Изучение свойств ферромагнетиков.

Цель работы: Изучение свойств ферромагнетиков; исследование динамической петли гистерезиса и кривой намагничивания; определение характеристик ферромагнетика – остаточной индукции, коэрцитивной силы, магнитной проницаемости и потерь энергии на перемагничивание.

Основные понятия.

Если в магнитное поле, образованное токами в проводах, ввести то или иное вещество, поле изменится. Это объясняется тем, что всякое вещество является магнетиком, т.е. способно под действием магнитного поля намагничиваться – приобретать магнитный момент. Намагниченное вещество создает свое магнитное поле В, которое вместе с первичным полем В, обусловленным токами проводимости, образует результирующее поле:

= ₀

Опыты показывают, что магнетики могут как усиливать, так и ослаблять внешнее поле. Все магнетики делятся по своим магнитным свойствам на три класса: диамагнетики, парамагнетики и ферромагнетики. Диа- и парамагнетики при внесении во внешнее магнитное поле намагничиваются слабо. Степень намагничивания магнетика характеризуется магнитным моментом единицы объема. Эту величину называют намагниченностью и обозначают .

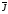По определению

_m ,

где - объем магнетика

_m – магнитный момент отдельной молекулы.

Суммирование проводится по всем молекулам в объеме .

Вектор индукции намагничивающего поля связан с вектором напряженности соотношением:

₀ =

где ₀ – магнитная постоянная

- магнитная проницаемость среды.

Векторы и пропорциональны друг другу:

,

где коэффициент пропорциональности, называемый магнитной восприимчивостью вещества. Это безразмерная величина, характерная для каждого данного магнетика.

По определению векторы и связаны соотношением:

Ферромагнетики. Ферромагнитными называют вещества, которые могут обладать спонтанной намагниченностью, т.е. намагничены уже при отсутствии внешнего магнитного поля.

Характерной особенностью ферромагнетиков является нелинейная зависимость и (рис 1).

J B

J_на

H H

Рис 1.1 Рис 1.2

На рис 1.1 приведена кривая намагничения ферромагнетика, ее называют кривой намагничения. На рис 1.2 привидена основная кривая намагничения на диаграмме , ввиду нелинейности зависимости для ферромагнетиков нельзя ввести магнитную проницаемость как определенную постоянную величину, характеризующую магнитные свойства каждого данного ферромагнетика. Магнитная проницаемость может достигать очень больших значений.

Величина В обращается в нуль лишь под действием поля Н_с , имеющего направление, противоположное полю, вызвавшему намагничивание. Величина Н_с называется коэрцитивной силой. При повышении температуры способность ферромагнетиков намагничиваться уменьшается, в частности, уменьшается намагниченность насыщения. При некоторой температуре, называемой температурой или точкой Кюри, ферромагнитные свойства исчезают.

При температурах, более высоких, чем температура Кюри, ферромагнетик превращается в парамагнетик. Физическую природу ферромагнетизма удалось понять только с помощью квантовой механики.

Это может быть пояснено с помощью следующей схемы:

Рис.

1.3

Железный кубик помещен в магнитное поле индукции , параллельное одной из его диагональных плоскостей (рис 1.3). Это поле образует с направлениями намагничивания в смежных областях углы и . Пусть угол будет меньше, чем угол . При этом области, которым соответствует угол , будут расти за счет областей с углом и при этом разделяющая стенка будет перемещаться вправо. На 3 рисунке имеется только две области, направление намагничивания которых расположены симметрично относительно оставшейся разделительной стенки. При дальнейшем увеличении индукции внешнего поля начинается новый процесс: направление вектора намагничивания изменяется и приближается к направлению внешнего поля. Этот “процесс поворота” заканчивается, когда весь кристалл равномерно намагнитится, т.е. наступает насыщение.

Порядок выполнения работы

1. Включили установку и осциллограф. С помощью ручек ЛАТРа на панели блока и «УСИЛЕНИЕ» на панели осциллографа добились, чтобы петля гистерезиса занимала значительную часть экрана, имела участок насыщения и была симметричной относительно начала координат.

2. Измерили в делениях масштабной сетки координаты вершины петли и координаты точек пересечения петли с осями X и Y.

3. Уменьшая ручкой ЛАТРа ток через катушку, зарегистрировали координаты вершин 5, 6 петель, каждый раз обращая внимание на их симметричное расположение относительно начала координат.

4. Произвели калибровку осей X и Y осциллографа. Измерили значение Х_m в делениях масштабной сетки, затем ко входу Y подключили напряжение и измерили высоту вертикальной линии Y_k.

Обработка результатов эксперимента.

Строим кривую намагничения в координитах (В,Н)

Измеряем площадь предельной петли гистерезиса S_m в делениях масштабной сетки осциллографа:

S_m = 24010^-6 (м²).

По средней линии вычислим длину окружности тороида (1):

L=

Рассчитываем площадь сечения:

Вычислим величины Н/X и В/Y по формулам:

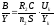
Используя известные(табличные) величины:

R₁ = 22 Ом , R₂ = 120 Ом , С = 2.2 мкФ , n₁ = 360 , n₂ = 150

и полученные величины:

X_m = 1.6 , Y_k = 2 , т.к. U_k = 0.1 В , то U_k/Y_k = 0.05 (В/дел)

Получаем:

22.04 ((А/м)/дел.)

(Тл/дел.)

Рассчитаем предельную магнитную проницаемость по формуле:

, где

- магнитная постоянная.

(Гн/м).

Так как X_c=0.6, то

Y_r=1, следовательно

Рассчитываем потери энергии за цикл перемагничивания по формуле:

W_n = S_m(B/Y)(H/X).

W_n = 240*10^-6 * 22.04*1.17 = 0.00619 (Дж).

Расчет погрешностей.

.

, .

=0,05 – погрешность определения амплитуды осциллографом в нормальных условиях эксплуатации.

ВЫВОД.

При выполнении данной работы изучил свойства ферромагнетиков; Исследовал динамическую петлю гистерезиса и кривой намагничивания; определил характеристики ферромагнетика – магнитную проницаемость, потери энергии на перемагничивание.

W = 0.00619 Дж

= 25424 Гн/м

В результате измерений возникла большая погрешность из-за не точности приборов.