7

Физический маятник

Цель работы: изучение гармонических колебаний; определение приведённой длины маятника и ускорения свободного падения.

Теоретические сведения

Простейшим типом колебаний является колебание, совершаемое по закону:

или

Основные характеристики колебаний — амплитуда, частота, период. Частота колебаний равна числу полных колебаний, совершаемых за единицу времени. Периодом колебаний называется промежуток времени, за который совершается одно полное колебание. Период связан с частотой соотношением .

Циклическая или круговая частота колебаний численно равна числу полных колебаний, за секунд: . Тело совершает гармонические колебания, когда на него действует другая сила, пропорциональная величине смещения от положения равновесия : , где k – коэффициент упругости. Знак “минус” указывает, что возвращающая сила направлена в другую сторону от направления смещения, то есть к положению равновесия.

Запишем для колеблющегося тела второй закон Ньютона: или . Уравнение можно переписать 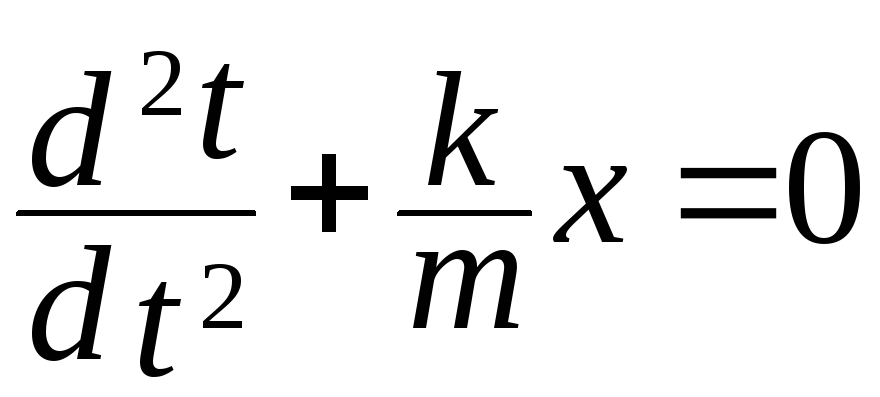и ввести обозначения 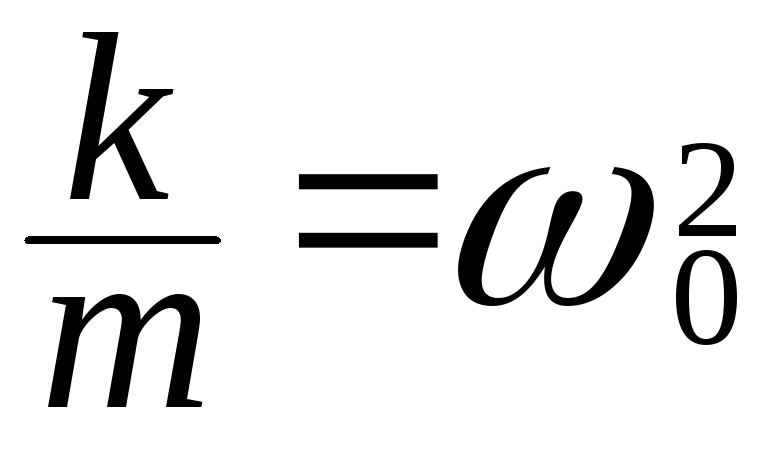. Тогда уравнение примет вид . Это и есть дифференциальное уравнение гармонических колебаний. Одним из решений такого уравнения является . Циклическая частота колебания называется циклической частотой собственных колебаний.

При гармонических колебательных движениях кинетическая энергия колеблющейся материальной точки непрерывно меняется. Меняется и потенциальная энергия взаимодействия между точкой и окружающей средой. Кинетическая энергия колеблющейся точки массой . Потенциальная энергия квазиупругих сил, отсчитываемая от положения равновесия данной материальной точки: , где - смещение колеблющейся точки от положения равновесия, - коэффициент квазиупругой системы. Полная энергия материальной точки, совершающей гармонические колебания с частотой и амплитудой A:

В процессе движения происходит непрерывный переход кинетической энергии в потенциальную и обратно, но полная энергия – величина постоянная, она пропорциональна квадрату колебаний. Собственные гармонические колебания – это идеальный случай колебаний, когда энергия системой не теряется, и амплитуда остается постоянной. В случае реальных колебаний энергия, переданная системе, постепенно расходуется на преодоления сил сопротивления, поэтому амплитуда колебаний уменьшается, колебания затухают, эти колебания называются затухающими. Их частота определяется свойствами колеблющейся системы – возвращающей силой, сопротивлением. Если сила сопротивления среды пропорциональна скорости колебания, т.е. , 2 закон Ньютона для колеблющейся точки запишем так: 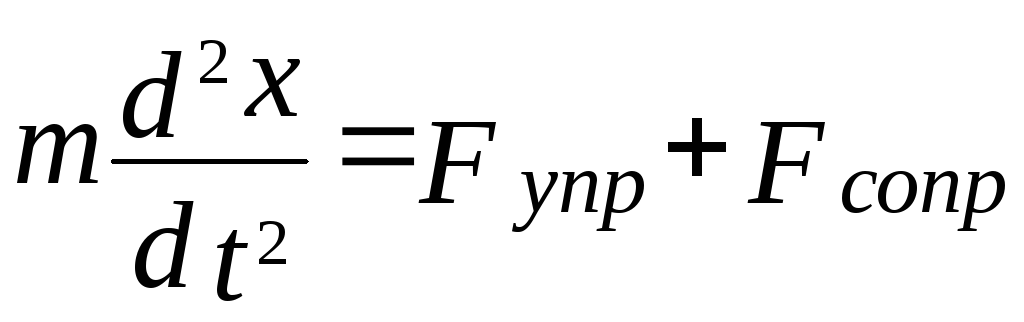или .

Введем обозначения: . Решение уравнения имеет вид . Амплитуда затухающих колебаний уменьшается по закону , частота затухающих колебаний .

Если , частота является минимальным числом и имеет место апериодический процесс.

В случае затухающих колебаний энергия убывает по закону .

Влечена отношения энергии и мощности потерь за время . Характеризует способность колебательной системы хранить энергию и называется добротностью: .

Добротность равна числу колебаний за время, за которое амплитуда уменьшается в раз.

Для изучения колебаний можно использовать физический или математический маятник.

Каждое тело подвешенное в точки, лежащей выше его центра тяжести, может колебаться и представляет собой физический маятник. На рисунке изображен физический маятник, отклоненный от положения равновесия. Через точку О перпендикулярную плоскости рисунка проходит неподвижная ось, вокруг которой совершаются колебания. С – центр тяжести маятника (точка в которой приложена сила тяжести mg). Момент силы mg относительно оси О равен: , где - расстояние от оси вращения до центра тяжести – точки С.

При малых углах отклонения, когда можно принять , основной закон динамики, вращательного движения, описывающий колебания такого маятника, можно записать в виде:

или 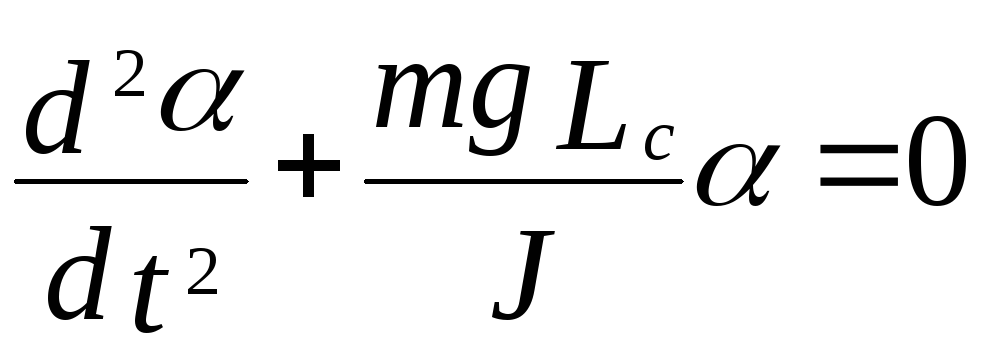, где J – момент энергии физического маятника относительно оси вращения.

Это уравнение аналогично уравнению , величина является квадратом круговой частоты гармонических колебаний:

Решением уравнения описывает гармонические колебания, совершаемые физическим маятником. Период колебаний: .

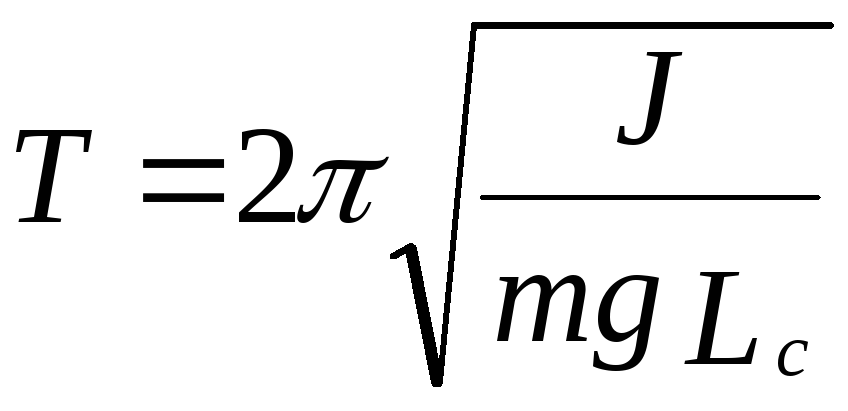Для математического маятника . Физический маятник колеблется так же (с тем же периодом), как и математический, описываемый , имеющий длину , где от 0 до с.

Приведенная длина физического маятника, который имеет тот же период колебаний, что и данный физический маятник.

Если к оси физического маятника подвесить грузик на нити такой длины, чтобы она была ровна приведенной длине такого физического маятника, то отклоненные на одинаковый угол физический маятник и грузик колеблются вмести так, что грузик находится в одной и той же точки физического маятника – его центр качания. Поэтому приведенная длина будет , т.е..

Методика проведения эксперимента

Обратный маятник состоит из стального стержня, на котором закрепляются опоры 1 и 2 в виде призм и грузы 3 и 4. Время N полных колебаний маятника измеряются секундомерами. В автоматическом режиме секундомер включается при срабатывании фотоэлемента датчика 6, выключается кнопкой СТОП.

Метод оборожного маятника основан на сопряженности двух его точек: подвеса и центра касания. Путем изменения расстояния между грузами (перемещением груза 3) добиваются такого расстояния, чтобы период колебания маятника при его переворачивании не менялся. При этом расстояние между опорами будет приведенной длиной маятника .

Теоретически рассчитать положение центра масс физического маятника можно для упрощении модели маятника, состоящей из невесомого стержня с закрепленным на нем материальными точками 3 и 4.

П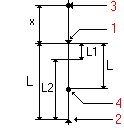орядок выполнения работы

Исходные данные:

Расстояние между спорами L=0.31м

Расстояние от опоры 1 до груза 4 l=0.15м

Масса маятника m=1.4м

Будем передвигать груз 3 и измерять время 10 полных колебаний, а результат записывать в таблицу, в которой:

x – расстояние от груза 3 до опоры 1

t1 – время 10 полных колебаний маятника, подвешенного за опору 1

t2 – время 10 полных колебаний маятника, подвешенного за опору 2.

№ эксперимента	х, м	t1, c	t2, c
1	0.04	10.42	10.71
2	0.05	10.60	10.85
3	0.06	11.02	11.07
4	0.07	11.58	11.29
5	0.08	12.22	11.90

Построим зависимость времени колебаний маятника на опорах 1 и 2 от положения груза 3.

По точки пересечения графиков находим хпр=0.062м.

Приведенная длина физического маятника определяется по формуле: .

Необходимо найти . Для этого установим груз 3 в положение хпр=0.062м и определим время 10 колебаний 10 маятника, повторим опыт несколько раз:

№ эксперимента	Хпр,м	10,с
1	0.062	11.20
2	0.062	10.94
3	0.062	11.10
4	0.062	11.16
5	0.062	10.94

Вычисляем среднее время отсюда =1.1068≈1.107с. Найдем

Рассчитаем положение центра масс маятника м м. Рассчитаем момент инерции при подвешивание на опоры 1 и 2:

Найдем ускорение свободного падения:

Расчет погрешности

Погрешность расчета приведенной длины физического маятника определяется по формуле: , где =0.05с – половина цены деления.

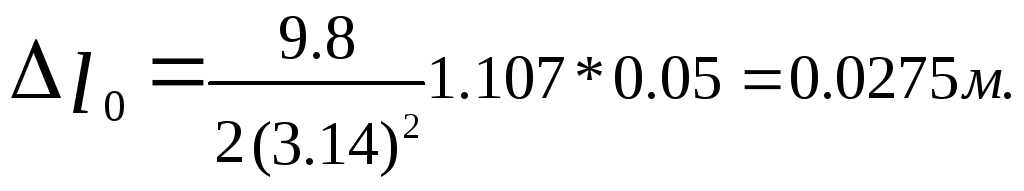
В формулах расчета положения центра масс погрешности и будут равны .

Расчет погрешности и относительно спор 1 и 2 =0.007, =0.0096

Погрешность определения ускорения свободного падения:

.

Вывод: определена поведенная длина физического маятника =0.30420ю0275м.

Определена ускорение свободного падения g=9.790.9.