Цель работы: изучение закона электромагнитной индукции, расчет индуктивности короткого соленоида; проверка закона Ома для цепи постоянного и переменного тока с индуктивностью и активным сопротивлением; экспериментальное определение индуктивности короткого соленоида и магнитной проницаемости сердечника.

Основные понятия

1. При любом изменении магнитного потока  через поверхность, ограниченную проводящим контуром, между точками 1 и 2 проводника возникает ЭДС индукции, численно равная скорости изменения магнитного потока (закон Фарадея):

(3.1)

Рис. 1.

Из уравнения (1) следует, что поток магнитной индукции может изменяться как при движении контура в стационарном магнитном поле, так и за счет изменения индукции магнитного поля во времени. Знак минус выражает правило Ленца: ток в контуре имеет всегда такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего этот ток.

В отсутствии внешнего магнитного поля электрический ток, текущий в контуре, создает вокруг себя магнитное поле, индукция которого по закону Био-Савара-Лапласа пропорциональна току в контуре. Если в контуре протекает переменный ток, то сцепленный с ним магнитный поток будет изменяться во времени и между точками 1 и 2 возникает ЭДС индукции. Данное явление называется самоиндукцией. Магнитный поток при самоиндукции пропорционален току в контуре

(3.2)

так что закон Фарадея можно записать в следующей форме:

(3.3)

Коэффициент пропорциональности L называется индуктивностью контура и зависит только от его геометрических размеров. Индуктивность определяется из закона Био-Савара-Лапласа в результате интегрирования по длине проводящего контура l с учетом выражения (2) для потока магнитной индукции:

, (3.4)

где =410^-7 Гн/м – магнитная проницаемость вакуума, - радиус-вектор, проведенный из элемента контура в элемент ds поверхности S, ограниченной данным контуром, индекс «n» означает проекцию векторного произведения на нормаль к поверхности.

2. Получим формулу для расчета индуктивности короткого соленоида, длина которого l соизмерима с его радиусом .

Индукция магнитного поля в точке 0 на оси соленоида, создаваемая участком намотки dx пропорциональна числу витков на данной длине:

, (3.5)

где b₀ – индукция, создаваемая одним витком, n – число витков на единице длины. В соответствии с законом Био-Савара-Лапласа ток, протекающий в элементе dl проводящего контура, создает в точке 0 индукцию

(3.6)

Интегрируя уравнение (6) по длине витка, получаем выражение для индукции магнитного поля, создаваемой одним витком:

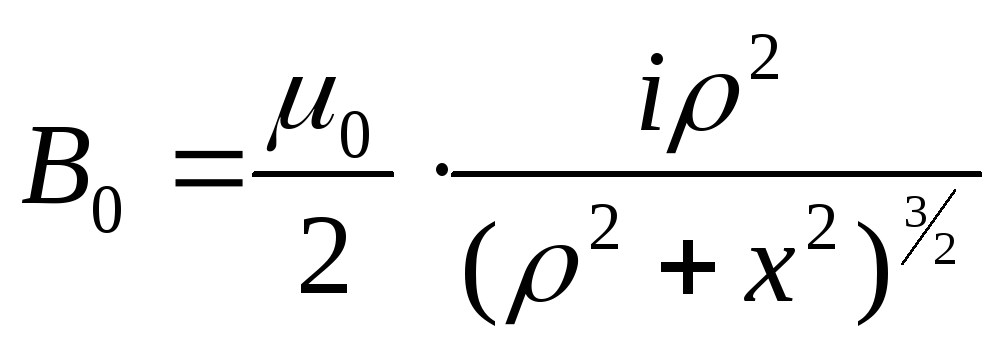(3.7)

В результате интегрирования (5) по всем значениям x в интервале от l₀ до l-l₀ и замены переменных x=ctg , получаем следующее выражение для индукции магнитного поля на оси соленоида:

(3.8)

При вычислении индукции магнитного поля реального соленоида необходимо учитывать не только зависимость B от l₀, но и неоднородность поля по сечению соленоида. Для расчета индуктивности короткого соленоида, магнитная индукция которого зависит от его сечения, можно использовать приближенную формулу:

(3.9)

Для длинного соленоида (l>>p) формула (9) существенно упрощается и имеет следующий вид:

(3.10)

Индуктивность катушки, заполненной магнетиком с магнитной проницаемостью, рассчитывается по формулам:

(3.11)

рис.2

(3.12)

3.Определим величину переменного тока в цепи, состоящей из катушки индуктивности с активным сопротивлением , подключённой к источнику переменного напряжения .

Этот ток изменяется по закону

(3.13)

Амплитуда тока и фаза определяются амплитудой, параметрами цепи , и частотой :

(3.14)

Из (3.14) следует, что ток в цепи отстаёт по фазе от приложенного напряжения на угол , который зависит от параметров цепи и частоты:

(3.15)

где - полное электрическое сопротивление цепи.

Зависимость амплитуды тока от выражает закон Ома для цепи переменного тока. Если , то по цепи течёт постоянный ток, для которого

(3.16)

МЕТОДИКА ЭКСПЕРИМЕНТА.

Экспериментальная установка состоит из двух истосчников постоянного и переменного токов: регулировка которых осуществляется потенциометром . Измерения токов и осуществляются амперметром .

Вольтметр измеряет напряжение на катушке индуктивности. В установке предусмотрены элементы, позволяющие измерять одним и тем же прибором характеристики переменного и постоянного тока.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ.

1. В положении переключателя «R» осуществить проверку закона Ома для цепи постоянного тока. При различных положениях ручки потенциометра зарегистрировать ток 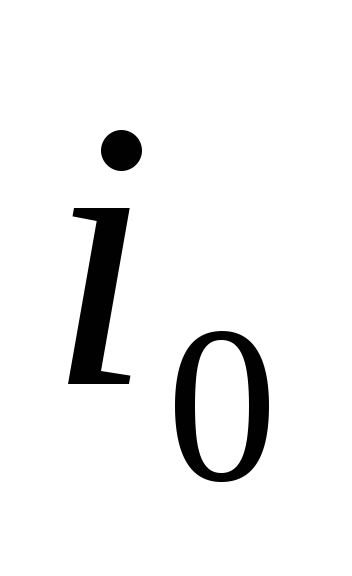и напряжение на активном сопротивлении катушки.

2. Снять зависимость тока в цепи переменного тока от напряжения на катушке в положении «Z» переключателя.

3. Аналогичные измерения в п.2 провести для катушки со стальным сердечником, который ввинчивается в катушку индуктивности на правой панели прибора.

ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА.

1. На основании результатов измерений определить величину активного сопротивления , используя метод наименьших квадратов для линеаризации функции :

(3.17)

где

(3.18)

где N- число измерений и .

2. Используя метод наименьших квадратов, аналогичным образом определить Z:

(3.19)

3. Вычислить индуктивность катушки без сердечника:

(3.20)

4. Вычисление п.п. 1-3 повторить для катушки с сердечником и найти .

5. Определить магнитную проницаемость сердечника, используя формулу:

(3.21)

6. Рассчитать индуктивность катушки по формуле (3.11), используя известные геометрические размеры соленоида. Сравнить теоретические и экспериментальные результаты.

РАСЧЁТ ПОГРЕШНОСТЕЙ.

1. Расчёт погрешности определения активного сопротивления катушки.

Вычисление активного сопротивления катушки и случайной состовляющей по имеющейся зависимости. Напряжения от тока осуществляется с помощью метода наименьших квадратов. При этом уравнение линейной регрессии имеет вид , где - угловой коэффициент наклона прямой, проходящей через начало координат. Этот коэффициент находится по формуле (11.8), где , , .

Погрешность определения углового коэффициента находится из соотношения (11.9).

Здесь необходимо также учесть приборные погрешности определения активного сопротивления по формуле:

,

где - класс точности амперметра, - класс точности вольтметра. Суммирование случайной с систематической погрешности осуществляется по формуле (11.10):

2. Расчёт погрешности определения полного сопротивления катушки.

Вычисление и по имеющейся зависимости амплитудного значения напряжения от амплитудного значения силы тока в цепи осуществляется аналогично тому, как это делалось в случае постоянного тока, с посмощью метода наименьших квадратов по формулам (11.8), (11.9), где , , . Учёт приборной погрешности

позволяет определить полную погрешность, что даёт:

3. Определение индуктивности и погрешности индуктивности катушки.

Формула для определения индуктивности:

Абсолютная погрешность определяется как погрешность косвенного измерения, что даёт:

.

Практическая часть

1. В положении переключателя «R» проверяем закон Ома для цепи постоянного тока. При различных положениях ручки потенциометра регистрируем ток i₀ и напряжение u₀ на активном сопротивлении катушки.

i0(mA)	32	56	76	108	132	160	188
u0(В)	1	2	3	4	5	6	7

*** r_L=0,037310³=37.3(Ом)

2. Снимаем зависимость тока в цепи переменного тока от напряжения на катушке u_m в положении «Z» переключателя.

im(mA)	21	39	54	66	81	96	108
um(В)	1	2	3	4	5	6	7

*** Z_L=0,061710³=61.7(Ом)

3. Аналогичные измерения в п.2 проводим для катушки со стальным сердечником, который ввинчивается в катушку индуктивности на правой панели прибора.

im(mA)	17	26	30	38	45	53	59
um(В)	1	2	3	4	5	6	7

*** Z=0,10910³=109(Ом)

Обработка результатов эксперимента

L₀=0.16(Гн)

L_=0,43(Гн)

=

по ф.(3.11) L=0,41(Гн)

Погрешности

(r_L)_n=41