лабораторная работа / закон динамики вращательного движения

Цель работы: изучить основной закон динамики вращательного движения, определить теоретические и экспериментальные значения момента инерции крестообразного маятника Обербека, изучить зависимость угловой скорости и момента силы от момента инерции

Ответы на вопросы для самопроверки:

1. Основной закон динамики вращения (II закон Ньютона для вращательного движения): Момент вращающей силы, приложенной к телу, равен произведению момента инерции тела на угловое ускорение.

2. Моментом силы F неподвижной точки О называется векторное произведение радиус-вектора r, проведенного из точки О в точку N приложения силы F, на саму эту силу..

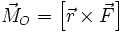
3. сумма произведений элементарных масс Δm_i , составляющих данное тело , на квадраты их растояний до оси вращения R, называют моментом инерции тела относительно данной оси вращения

угловое ускорение – это скорость изменения угловой скорости в единицу времени ε=

4. Физический смысл момента инерции: момент инерции играет при вращательном движении тела такую же роль, какую масса при поступательном движении, т.е. момент инерции является мерой инертности тела при вращательном движении.

5. Направление вектора ω совпадает по направлению с осью вращения и определяется по правилу правого винта. Вектор углового ускорения направлен по оси вращения в ту же сторону, что и вектор ω, при ускоренном движении, и в противоположную сторону при замедленном. Момент внешних сил M сонаправлен с моментом импульса L. dL=Mdt

6. Вращательное движение маятника Обербека описывается основным законом динамики вращательного движения, из которого момент инерции определяется как:

где М_Т – момент натяжения нити: где r – радиус шкива, заменим ε и a через величины h и t, для этого используем уравнение пройденного пути при равноускоренном движении:

. Используя полученные соотношения окончательно найдем: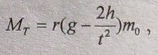

№	m0, кг	r, м	h, м	t, с	ε	M
1	0,312	0,035	0, 75	7,71	0,72	0,108
2	0,581			5,15	1,61	0,202
3	0,656			5,03	1,69	0,228
4	0,756			4,41	2,2	0,262
5	1,025			3,7	3,13	0,354

Вычисления:

1. ε==0,72 1/с² М==0,108 кг*м²/с²

2. ε=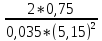=1,61 1/с² М==0,202 кг*м²/с²

3. ε==1,69 1/с² М==0,228 кг*м²/с²

4. ε==2,2 1/с² М==0,262 кг*м²/с²

5. ε==3,13 1/с² М==0,354 кг*м²/с²

№	r м	m кг	h м	R м	R2 м2	t с	I
1	3,5	0,756	0,75	0,05	0,0025	3,3	0,135
2				0,1	0,01	4,05	0,819
3				0.15	0,0225	4,2	1,98
4				0,2	0,04	5,54	6,15
5				0,25	0,0625	5,79	10,5

Вычисления:

1. I=*0,756=0,135 кг*м²/с²

2. I=*0,756=0,819 кг*м²/с²

3. I=*0,756=1,98 кг*м²/с²

4. I=*0,756=6,15 кг*м²/с²

5. I=*0,756=10,5 кг*м²/с²

Вывод: изучили основной закон динамики вращательного движения, определили теоретические и экспериментальные значения момента инерции крестообразного маятника Обербека, изучили зависимость угловой скорости и момента силы от момента инерции