4

Цель работы

В ходе эксперимента вычислить показатель адиабаты и погрешность при его нахождении.

Методика эксперимента

Экспериментальная установка состоит из большого стеклянного баллона 1 объёмом V (V = 10л.) с воздухом, соединённого с манометром - 2 и насосом - 3. С помощью клапана 5 в насадке 4 баллон может сообщаться с атмосферой и с помощью клапана 6 – с насосом. Разность уровней жидкости в коленах манометра показывает превышение давления P в баллоне над атмосферным.

Метод Клемана-Дезорма определения показателя адиабаты основан на исследовании некоторой массы воздуха, мысленно выделенной в баллоне, последовательно проходящей через три состояния, причём из 1-го во 2-ое состояние воздух переходит путём адиабатического расширения, и из 2-го в 3-е путём изохорического нагревания.

С помощью насоса в баллон накачивают некоторую массу воздуха. Вследствие произведённой работы (при накачивании) воздух в баллоне нагреется. До начала опыта необходимо подождать несколько минут, чтобы в результате теплообмена температура в баллоне сравнялась с температурой окружающей среды. При этом давление в баллоне несколько снизится, т.к. давление пропорционально температуре (P = nkT).

Рассмотрение процесса начнём с того момента, когда температура и давление в баллоне установились. Выделенная часть воздуха в баллоне в начале процесса будет характеризоваться P₁ (выше атмосферного), V₁, T₁ (температура окружающей среды), что соответствует точке I на диаграмме состояний.

П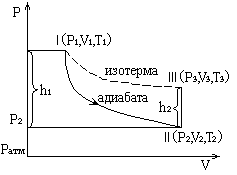 роизведём адиабатическое расширение воздуха в баллоне, соединив объём баллона с атмосферой. Часть воздуха выйдет из баллона, а выделенная масса воздуха расширится. Это расширение можно считать почти адиабатическим, если оно происходит быстро и теплообмен с окружающей средой произойти не успевает. Такой процесс приближённо можно считать равновесным и изобразить на диаграмме.

На рисунке процесс расширения изображён отрезком адиабаты I-II. Давление в баллоне сравнивается с атмосферным, а температура понижается. Параметры выделенной части воздуха принимают значения: P₂ (атмосферное давление), V₂, T₂ (ниже температуры окружающей среды). Параметры воздуха в начале и в конце опыта связаны уравнением адиабаты:

(1)

После адиабатического нагревания в течение 2-3-х минут произойдёт теплообмен между окружающей средой и воздухом в баллоне. Температура в баллоне поднимется до температуры окружающей среды, а давление повысится. Процесс изобразится отрезком изохоры II-III. Параметры газа примут значения P₃, V₂, T₁ (окружающей среды).

Сравнивая конечное состояние выделенной части воздуха III с исходным I, можно заметить, что они находятся при одной и той же температуре T₁, такие состояния связаны уравнением изотермы:

(2)

Для определения показателя адиабаты возведём уравнение (2) в степень  и разделим почленно на уравнение (1):

или (3)

Логарифмируя уравнение (3), получим:

(4)

Эту формулу упростим, исходя из условий эксперимента. Выразим давление воздуха в баллоне через разность уровней жидкости в коленах манометра h. Обозначим атмосферное давление H, добавочное давление в состоянии I буквой h1 и добавочное давление в состоянии III буквой h₂. Тогда P₁ = H + h₁, P₂ = H, P₃ = H + h₂, где h₁ и h₂ << H.

Подставим эти значения в уравнение (4):

(5)

Поскольку , при x << 1, получим , и

Подставляя эти формулы в (5), для показателя адиабаты имеем:

(6).

Порядок выполнения работы

1. Накачиваем с помощью насоса воздух в баллон до давления 0,8 – 0,9 от предельного по шкале манометра. Ждем около 5 минут, чтобы падение давления поэтапно прекратилось. Клапан 5 должен быть закрыт. Отсчитываем разность уровней h₁.

Для измерения величины h₂ можно использовать 2 способа:

2. 1-й способ. Производим адиабатическое расширение. Для этого на 1-2 секунды нажимаем клапан. Ждем 1-2 минуты, затем снимаем новую разность уровней h₂.

3. Измерение п.2 повторяем 9 раз и для каждого измерения вычисляем  по формуле (6).

4. 2-й способ. Нажимаем клапан и держим открытым время t_i (1-5 секунд). Отпускаем клапан и ждем 1-2 минуты, определяем полученную разность h_2i.

5. Измерения t_i и h_2i проводим 5 раз при разных значениях t_i и неизменном значении h₁.

	№ эксперимента
	1	2	3	4	5	6	7	8	9	10
h1	0.160	0.155	0.173	0.166	0.168	0.168	0.175	0.176	0.174	0.168
h2	0.045	0.043	0.048	0.046	0.045	0.047	0.050	0.046	0.047	0.047
	1.391	1.40186	1.384	1.383	1.365	1.388	1.400	1.353	1.370	1.385

	№ эксперимента
	1	2	3	4	5	6	7	8	9	10
h1k	6,40	-3,60	1,40	11,40	0,40	-9,60	-3,60	-8,60	-5,60	11,40
h2k	0,7	1,7	-0,3	2,7	-0,3	-2,3	0,7	-2,3	-0,3	-0,3

Обработка результатов эксперимента

1. Для значений находим среднее значение .

2. V₂ = V₀ = 10л. = 0,01м³ – объём баллона, T₁ = T₀ = 300K – температура воздуха и P₂ = P₀ = 10⁵ Па – давление в лаборатории.

Определяем количество молей газа в баллоне:

Определяем внутреннюю энергию газа:

где i – количество измерений, в которых могут перемещаться молекулы газа.

3. По данным исходного состояния и значению  вычисляем:

Расчёт погрешностей

П огрешность вычисления показателя адиабаты  рассчитывается по формуле расчёта погрешности косвенных измерений:

Где h₁ и h₂ определяются по методике расчёта погрешностей прямых измерений:

где N-число измерений, C_N-коэффициент Стьюдента для N (N = 10) измерений (C₁₀ = 2,3).

Вывод

Средний показатель адиабаты , что близко к реальному значению. Допущенная погрешность   0.43 .