Цель работы

Изучение законов динамики вращательного движения; теоретическое и экспериментальное определение момента инерции крестообразного маятника Обербека; изучение зависимостей угловой скорости и момента силы от момента инерции.

Основные понятия.

Моментом силы F относительно точки О называется векторное произведение радиус-вектора , проведенного из точки О в точку приложения силы, на вектор силы : .

М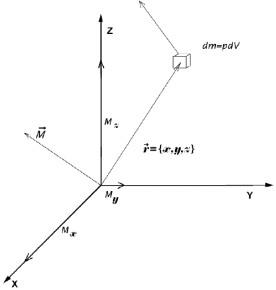оментом силы относительно оси называется скалярная величина, равная проекции на данную ось вектора момента силы относительно какой-либо точки той же оси.

Если рассмотреть отдельную материальную точку массой dm, вращающуюся вокруг оси на расстоянии r, то ее момент инерции равен J=dmr². Твердое тело можно мысленно представить как совокупность большого числа n материальных точек dm_i и просуммировать моменты инерции всех точек относительно данной оси:

(1)

Если тело однородно, то dm=dV, где  - плотность, dV – элементарный объем. Тогда момент инерции всего тела может быть рассчитан по формуле:

(2)

Если известен момент инерции тела относительно оси, проходящей через центр инерции (центр масс) тела J₀, то можно вычислить момент инерции тела относительно оси с помощью теоремы Штейнера: момент инерции J относительно произвольной оси вращения равен сумме моментов инерции J₀ относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния a между осями:

J=J₀+ma² (3)

Покажем, как, пользуясь теоремой Штейнера и выражением для момента инерции цилиндра, полученным из (2) после интегрирования по объему, можно рассчитать момент инерции крестообразного маятника Обербека.

Момент инерции всего маятника относительно оси вращения равен сумме моментов инерции четырех стержней с цилиндрическими грузами на них, момента инерции втулки, в которой крепятся стержни, и момента инерции барабана:

J=J_вт+J_б+4(J_ст+J_гр) (4)

У втулки и барабана ось вращения проходит через их центр масс, это цилиндрические тела, поэтому:

Момент инерции стержня длиной l_ст, относительно оси, проходящей через его конец и перпендикулярный ему

Момент инерции грузов найдем, считая грузы материальными точками массой m, так как их рамеры малы по сравнению с расстоянием до оси вращения: J_гр=m_грx², где x – расстояние от центра груза до оси вращения. Все части маятника – цилиндры, поэтому их массы запишутся , где =7.810³ кг/м³ – плотность стали, d – диаметр цилиндра, l – его высота или длина.

(5)

Момент силы , момент инерции J и угловое ускорение связаны основным законом динамики вращательного движения: .

Учитывая, что , этот закон можно записать в виде:

(6)

где - момент импульса (количества движения) тела.

Методика эксперимента

Маятник Обербека состоит из четырех стержней, расположенных под прямым углом друг к другу, втулки и барабана, на который наматывается нить. По стержням могут перемещаться грузы равной массы, которые могут быть укреплены в любых точках стержня.

Маятник приводится во вращение с помощью груза m, подвешенного на шнуре, который наматывается на барабан. Если груз поднять на некоторую высоту h, то он будет опускаться, вращая барабан, а с ним и весь маятник.

1. Момент инерции маятника можно определить из основного закона динамики вращательного движения , где - момент силы, приводящий маятник во вращение, - его угловое ускорение. Выразим момент силы и угловое ускорение через величины, легко измеряемые на опыте. Момент силы – это произведение силы на плечо ее приложения, то есть радиус барабана r_б. Силой, вращающей маятник, является сила натяжения шнура. Для определения силы натяжения шнура рассмотрим силы, действующие на груз.

Со стороны Земли действует сила тяжести mg, со стороны шнура – сила натяжения F_н. По второму закону Ньютона , где - линейное ускорение груза. Спроектируем на вертикальную ось:

(7)

Ускорение груза a найдем из формулы равноускоренного движения h=at²/2, где h – высота, с которой опускается груз, t – время движения. Получим a=2h/t². Окончательно момент силы:

(8)

Угловое ускорение  маятника и барабана найдем, связав его с линейным ускорением груза a. Так как шнур плотно намотан на барабан, он сообщает точкам его поверхности то же линейное ускорение, которое имеет груз. Поэтому a=r_б одновременно является линейным ускорением груза и точек поверхности барабана. Тогда:

(9)

Подставив (10) и (9) в (7), получим , откуда

(10)

2. С помощью маятника Обербека можно опытным путем получить связь между  и моментом инерции J.

Меняя расстояние от грузов на стержнях до оси вращения, мы тем самым меняем момент инерции маятника. Поэтому, в соответствии с основным законом динамики вращательного движения, если J₁>J₂, должно получиться ₁<₂. Угловое ускорение в каждом случае рассчитывается через время падения (9). При постоянном моменте силы M:

M=J₁₁=J₂₂. (11)

. Установка позволяет определить момент сил трения, возникающих в трущихся частях на оси вращения. Груз m, поднятый на высоту h относительно нижней точки, сначала опускается до этой точки, а затем из-за инертности вращательного движения маятника вновь поднимается до высоты h₁<h.

Запишем закон сохранения энергии с учетом сил трения для одного такого цикла:

mgh=mgh₁+M_Тр,

где  - угол поворота маятника за все время движения.

Так как , то получим: . Отсюда:

(12)

Порядок выполнения работы

Для определения момента инерции:

1. Закрепляем грузы на концах стержней маятника Обербека и 3 раза измеряем t – время падения груза с высоты h.

2. Уменьшаем на одинаковую величину расстояние от грузов до оси вращения и повторяем п.1.

x(c)	t1(c)	t2(c)	t3(c)	(c)
0.2	15.5	17	16.5	16.3
0.05	10	11	11	10.6

Для определения момента сил трения:

1. Измеряем высоту h падения груза относительно нижней точки.

2. Отпускаем груз и измеряем высоту h₁, на которую поднимется груз при остановке маятника.

3. Повторяем опыт 3 раза и находим среднее значение .

h=0.6 м

h1=0.23 м

h1=0.24 м

h1=0.24 м

=0.237 м

Обработка результатов эксперимента

_стали = 7,710³ кг/м³; H = 2,510^-2 м; a = 2,510^-2 м/c²; H₀ = 8,310^-2 м; R = 1,010^-2 м.

1. По формуле (10) определяем J для каждого опыта: J₁=0.057, J₂=0.068, J₃=0.064 – при x=0.2; J₁=0.024, J₂=0.028, J₃=0.028 – при x=0.05.

Определяем среднее значение при каждом положении x: =0.063 кгм²; =0.027 кгм².

Строим график зависимости момента инерции маятника от положения грузов на стержнях (x).

2. По формуле (5) при тех же значениях x теоретически рассчитываем и строим зависимость (x).

x	0,2	0,05
(x)	0,1879	0,0366

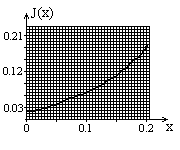
3. По формуле (9) определяем  и проверяем выполнение соотношения (11).

J₁₁=2,8510^-2, J₂₂=2,8810^-2 J₁₁J₂₂

4. По формуле (12) рассчитываем значение M_Тр. M_Тр=1.2510^-2.

Расчет погрешностей

Абсолютная погрешность J измерения момента инерции рассчитывается по формуле для косвенных измерений:

Величина t определяется как случайная погрешность прямого измерения.

,

x	t	J
0.2	0.054	0.001
0.05	0.183	0.0014

где С_N – коэффициент Стьюдента, t_i – время, полученное при i-ом измерении, - среднее время из N измерений, - среднее значение момента инерции.

Погрешность измерения момента сил трения рассчитывается по формуле для косвенного измерения:

где при заданном значении h величина h определяется как приборная погрешность (половина цены деления измерительной линейки), а h₁ для N измерений вычисляется по формуле Стьюдента:

где - среднее значение высоты подъема, h_1k – высота подъема при k-ом измерении.

h₁=0.006, M_Тр=0.002

Проделав все задания, относящиеся к данной лабораторной работе и сделав все необходимые вычисления, мы можем сделать ряд выводов:

• с увеличением расстояния между осью вращения и положением цилиндров, момент инерции маятника J увеличивается;

• угловая скорость вращения маятника обратно пропорционально зависит от величины t, то есть чем меньше время прохождения расстояния h^’ , тем угловая скорость больше, иначе – меньше;