20. II начало термодинамики

Обратимый процесс. Приведенное количество теплоты. Энтропия. Неравенство Клаузиуса. Статистический смысл II начала термодинамики. Закон Больцмана.

Обратимый процесс–это термодинамический процесс, если при протекании его, как в прямом, так и в обратном направлениях, в системе и окружающей среде, никаких изменений не происходит.

Приведённое количество теплоты величина , таким образом для цикла Карно имеем, что алгебраическая сумма приведённых количеств теплоты равна 0. Приведённое количество теплоты для бесконечно малого процесса. Строгий теоретический расчёт показывает, что для любого обратимого кругового процесса сумма приведённых количеств теплоты равна 0. Математически это записывается так:. Из высшей математики известно, что из равенства нулю интеграла, взятого по замкнутому контуру следует, что подынтегральное выражение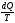есть полный дифференциал некоторой функции, которой определяется только состоянием системы, и не зависит от пути перехода в это состояние.

Энтропия

Свойства энтропии. Энергия свободная и связанная. Вычисление энтропии. Теорема Нернста (III начало термодинамики).Функция состояния, дифференциалом которой является Q/T, называется энтропией и обозначается S. _.При изотермическом процессе (t₁=t₂) _. При изохорном процессе(V₁=V₂)

Согласно Больцману (1872), энтропия системы в термодинамическая вероятность связаны между собой следующим образом: S = k lnW,

Свойства энтропии:

1.Энтропия обладает свойством аддитивности: энтропия системы равна сумме энтропий тел, входящих в систему.

2. энтропия замкнутой системы может либо возрастать (в случае необратимых процессов), либо оставаться постоянной (в случае обратимых процессов).

Неравенство Клаузиса.

Функция состояния, дифференциалом которой является Q/T, называется энтропией и обозначается S. Соотношения S=0 и S>0 можно представить в вида неравенства Клаузиуса S0, т. е. энтропия замкнутой системы может либо возрастать (в случае необратимых процессов), либо оставаться постоянной (в случае обратимых процессов).

Статистический смысл второго начала термодинамики

Классические статистики. Термодинамическая вероятность.

Формула Больцмана S = k lnW позволяет объяснить постулируемое вторым началом термодинамики возрастание энтропии в замкнутой системе при необратимых процессах: возрастание энтропии означает переход системы из менее вероятных в более вероятные состояния. Таким образом, формула Больцмана позволяет дать статистическое толкование второго начала термодинамики. Оно, являясь статистическим законом, описывает закономерности хаотического движения большого числа частиц, составляющих замкнутую систему.

Термодинамическая вероятность W состояния системы – это число способов, которыми может быть реализовано данное состояние макроскопической системы, или число микросостояний, осуществляющих данное макросостояние (по определению, W1, т. е. термодинамическая вероятность не есть вероятность в математическом смысле (последняя 1!)).

Согласно Больцману, энтропия системы в термодинамическая вероятность связаны между собой следующим образом: S = k lnW, где k – постоянная Больцмана. Таким образом, энтропия определяется логарифмом числа микросостояний, с помощью которых может быть реализовано данное макросостояние. Следовательно, энтропия может рассматриваться как мера вероятности состояния термодинамической системы.

Закон Больцмана о равномерном распределении энергии по степеням свободы молекул: для статистической системы, находящейся в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная kT/2, а на каждую колебательную степень свободы – в среднем энергия, равная kT. Колебательная степень «обладает» вдвое большей энергией потому, что на нее приходится кинетическая и потенциальная энергия, причем средние значения кинетической и потенциальной энергий одинаковы. Таким образом, средняя энергия молекулы гдеi – сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы: i=i_пост+i_вращ+2i_колеб.. В классической теории рассматривают молекулы с жесткой связью между атомами; для них i совпадает с числом степеней свободы молекулы