17.Теплоемкость

Теплоемкость газа. Молярная и удельная теплоемкость (определения и единицы измерения). Теплоемкость при постоянном объеме, температуре и давлении. Формула Майера.

Теплоемкостью какого – либо тела называется величина, равная количеству теплоты, которое нужно сообщить телу, чтобы повысить его температуру на 1К.

C=dIQ/dT

Где d^IQ –количество теплоты, сообщение которого повышает температуру тела на dT.

Молярная теплоемкость C_v, при постоянном V равна изменению внутренней энергии 1 моль газа при нагревании его на 1ºС.

Cv=dUм/dT

Удельная теплоемкость-это теплоемкость единицы массы вещества.

Cp=Cv+R

Формула Майера

Теплоемкость при постоянном объеме, температуре и давлении

При V=const, C=C_v

При p=const, C=C_p

При T=const, C=∞

18.Применение первого начала термодинамики к изопроцессам

Изотермический, изохорический и изобарический процесс. Количество теплоты, работа и внутренняя энергия при этих процессах. Графики процессов.

Изохорный процесс (V=const). Диаграмма этого процесса (изохора) в координатах р, V изображается прямой, параллельной оси ординат, где процесс 1–2 есть изохорное нагревание, а 1–3 – изохорное охлаждение.

При изохорном процессе газ не совершает работы над внешними телами, т. е. _. Следовательно, из первого начала термодинамики () для изохорного процесса следует, что вся теплота, сообщаемая газу, идет на увеличение его внутренней энергии:_. т.е. Тогда для произвольной массы газа получим

Изобарный процесс (p=const). Изобара в координатах р, V изображается прямой, параллельной оси V. При изобарном процессе работа газа при увеличении объема от V₁ до V₂  равна и определяется площадью заштрихованного прямоугольника

Если использовать уравнение Клапейрона–Менделеева для выбранных нами двух состояний, то _, откуда работа изобарного расширения _. В изобарном процессе при сообщении газу массой m количества теплоты его внутренняя энергия возрастает на величинуПри этом газ совершит работу, определяемую выражением_.

Изотермический процесс (T=const). Изотермический процесс описывается законом Бойля–Мариотта: pV = const. Поэтому изотерма в координатах р, V представляет собой гиперболу, расположенную на диаграмме тем выше, чем выше температура, при которой происходит процесс.

Исходя из выражений инайдем работу изотермического расширения газа: _. Taк как при T=const внутренняя энергия идеального газа не изменяется: _. то из первого начала термодинамикиследует, что для изотермического процесса_. т. е. все количество теплоты, сообщаемое газу, расходуется на совершение им работы против внешних сил: Следовательно, для того чтобы при расширении газа температура не понижалась, к газу в течение изотермического процесса необходимо подводить количество теплоты, эквивалентное внешней работе расширения.

19.Адиабатический процесс

Определение. Уравнение Пуассона. Показатель адиабаты. Количество теплоты, работа и внутренняя энергия при этом процессе. Графическое представление процесса.

Адиабатическим называется процесс, при котором отсутствует теплообмен (Q=0) между системой и окружающей средой. К адиабатическим процессам можно отнести все быстропротекающие процессы. Диаграмма адиабатического процесса (адиабата) в координатах р, V изображается гиперболой .

Вычислим работу, совершаемую газом в адиабатическом процессе. Запишем уравнение в виде_. Если газ адиабатически расширяется от объема V₁ до V₂, то его температура уменьшается от T₁ до T₂ и работа расширения идеального газа _. Применяя те же приемы, что и при выводе формулы TV ^-1=const, выражение для работы при адиабатическом расширении можно преобразовать к виду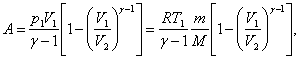где. Работа, совершаемая газом при адиабатическом расширении1–2 (определяется площадью, заштрихованной на рисунке.

Уравнение Пуассона (вывод):

Из первого начала термодинамики (Q = dU+A) для адиабатического процесса следует, что , т. е. внешняя работа совершается за счет изменения внутренней энергии системы. Используя выраженияA = pdV и , для произвольной массы газа перепишем уравнение в виде_. Продифференцировав уравнение состояния для идеального газа pV=m/MRT, получим _. Исключим из итемпературуT: _. Разделив переменные и учитывая, что С_P/С_V= , найдем _. Интегрируя это уравнение в пределах от p₁ до p₂ и соответственно от V₁ до V₂, а затем потенцируя, придем к выражению или . Так как состояния 1 и 2 выбраны произвольно, то можно записать pV^ = const. Полученное выражение есть уравнение адиабатического процесса, называемое также уравнением Пуассона.

Q=∆U+A

Количество теплоты

– 1-ый Закон термодинамики:

Теплота, сообщаемая системе идет на увеличение ее внутренней энергии на совершение системой А против внешних сил.

Работа

Найдем в общем виде внешнюю А, совершенную газом при изменении его объема. Рассмотрим газ, заключенный под поршнем. Газ расширяясь, передвигает поршень, на расстояние dl, при этом газ совершит работу:

A = pdV

Внутренняя энергия при этом процессе

Внутренняя энергия системы тел равна сумме внутренних энергий, образующих систему тел.

n U=∑ Ui i=1