
- •35. Самостоятельный газовый разряд, его типы и применение.
- •36. Плазма, ее свойства и применение.
- •37. Магнитное поле. Опыты Эрстеда. Магнитный момент витка с током.
- •38. Вектор магнитной индукции. Его связь с магнитной напряженностью.
- •39. Графическое изображение магнитного поля. Отличие линий магнитного поля от линий электростатического поля.
- •40. Закон Био-Савара-Лапласа. Магнитное поле прямого тока.
- •41. Закон Био-Савара-Лапласа. Магнитное поле в центре кругового проводника с током.
- •42. Взаимодействие проводников с током. Закон Ампера.
- •43. Магнитное поле движущегося заряда.
- •44. Действие магнитного поля на движущийся заряд. Сила Лоренца.
- •45. Движение заряженных частиц в магнитном поле. Ускорители элементарных частиц.
- •46. Эффект Холла.
- •47. Циркуляция вектора магнитной индукции. Ее сравнение с циркуляцией напряженности электростатического поля.
- •48. Магнитный поток. Теорема Гаусса для магнитного поля.
- •49. Работа по перемещению проводника и контура с током в магнитном поле.
- •50. Явление электромагнитной индукции. Закон Фарадея. Правило Ленца.
- •51. Вывод закона Фарадея из закона сохранения энергии.
- •52. Индуктивность контура. Самоиндукция. Э.Д.С. Самоиндукции.
- •53. Явление взаимной индукции. Принцип работы трансформатора.
- •54. Энергия магнитного поля. Плотность энергии магнитного поля.
- •55. Магнетики. Молекулярные токи. Магнитные моменты атомов.
- •56. Диа- и парамагнетики. Их намагниченность.
- •58. Напряженность магнитного поля. Магнитная проницаемость вещества.
- •57. Природа ферромагнетизма. Свойства ферромагнетиков.
- •60. Вихревое электрическое поле.
- •61. Ток смещения.
- •62. Уравнения Максвелла для электромагнитного поля.
- •66. Дифференциальное уравнение электромагнитной волны. Плоские электромагнитные волны.
- •67. Энергия и импульс электромагнитных волн. Вектор Умова-Пойнтинга.
- •68. Излучение диполя. Применение электромагнитных волн.
- •59. Типы жидких кристаллов. И т.Д.
- •64. Свободные затухающие колебания в колебательном контуре.
- •63. Свободные гармонические колебания в колебательном контуре.
- •64. Вынужденные колебания в электрических цепях.
- •1. Электрический заряд. Опыты Милликена. Закон сохранения заряда.
- •2. Закон Кулона.
- •3. Электростатическое поле. Напряженность электростатического поля. Принцип суперпозиции.
- •4. Графическое изображение электростатического поля. Поток вектора напряженности.
- •5. Электрический диполь. Поле диполя.
- •10. Потенциал электростатического поля.
- •11. Связь потенциала с напряженностью электростатического поля.
- •12. Типы диэлектриков. Поляризация диэлектриков. Виды поляризации.
- •14. Электрическое смещение. Теорема Гаусса для электростатического поля в диэлектрике.
- •16. Проводники в электростатическом поле. Граничные условия на границе «проводник-вакуум».
- •17. Электроемкость уединенного проводника. Единица электроемкости.
16. Проводники в электростатическом поле. Граничные условия на границе «проводник-вакуум».
Проводники - это вещества, в которых есть свободные носители зарядов, способные перемещаться под действием электрического поля. В случае металлических проводников свободными носителями заряда являются валентные электроны. Далее будем говорить о металлических проводниках, в которых носителями свободных зарядов являются электроны.
Электроны в
проводнике способны перемещаться под
действием сколь угодно малой силы
т.к.
![]() ,
то для равновесия (покоя) электронов в
проводнике необходимо, чтобы:
,
то для равновесия (покоя) электронов в
проводнике необходимо, чтобы:
1)
напряженность поля внутри проводника
равнялась нулю:
![]() .
(1) Поскольку
.
(1) Поскольку![]() =
-grad
=
-grad
![]() ,
[см.
(3.14)], то
равенство нулю
,
[см.
(3.14)], то
равенство нулю
![]() означает, что потенциал внутри
проводника должен быть постоянным, т.
е.
означает, что потенциал внутри
проводника должен быть постоянным, т.
е.
![]() = const .
(2) Из
(2) следует,
что поверхность проводника и весь
проводник являются эквипотенциальной
поверхностью;
= const .
(2) Из
(2) следует,
что поверхность проводника и весь
проводник являются эквипотенциальной
поверхностью;
2)
напряженность поля на поверхности
проводника должна быть в каждой точке
направлена по нормали к поверхности,
т. е.
![]() ,а касательная
составляющая
,а касательная
составляющая
![]() (3)
(3)
3)
Поскольку внутри заряженного проводника
электрическое поле отсутствует, то
согласно теореме Гаусса
–
Остроградского, это означает, что сумма
зарядов внутри него равна нулю.
Следовательно, все
(нескомпенсированные)
заряды располагаются на поверхности
проводника с поверхностной плотностью
![]() .
.
Используя теорему
Гаусса
-
Остроградского, легко показать, что
вблизи поверхности заряженного проводника
E =
![]() . (4)
. (4)
Проводник во внешнем электростатическом поле
 При
внесении незаряженного проводника
в электрическое поле, изображенное
штриховыми линиями на рис.
1, положительные
заряды будут перемещаться по направлению
При
внесении незаряженного проводника
в электрическое поле, изображенное
штриховыми линиями на рис.
1, положительные
заряды будут перемещаться по направлению
![]() ,
а отрицательные
- против
поля
,
а отрицательные
- против
поля
![]() .
В результате этого у концов проводника
возникают индукционные заряды
противоположных знаков. Они создают
поле, направленное против внешнего
так, что внутри проводника линии
напряженности будут разорваны поверхностью
проводника, заканчиваясь на индуцированных
отрицательных зарядах и начинаясь на
индуцированных положительных (см.рис.1.
сплошные линии).
.
В результате этого у концов проводника
возникают индукционные заряды
противоположных знаков. Они создают
поле, направленное против внешнего
так, что внутри проводника линии
напряженности будут разорваны поверхностью
проводника, заканчиваясь на индуцированных
отрицательных зарядах и начинаясь на
индуцированных положительных (см.рис.1.
сплошные линии).
Граничные условия
для векторов
![]() и
и![]()
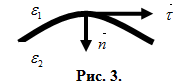
Из теоремы
Гаусса-Остроградского
(9) для поля
в диэлектрике, на границе раздела двух
диэлектриков, (см. рис.
3), имеем
![]() откуда
откуда![]() E
E![]() =
=![]() E
E![]() .
.
![]() =
=![]() ,
откудаЕ
,
откудаЕ![]() = Е
= Е![]() .
.
Таким образом, на границе раздела двух диэлектриков касательные составляющие напряженности электрического поля изменяются непрерывно, а нормальные составляющие - скачкообразно.
Заключение:
С учетом того, что напряженность поля
в диэлектрике E![]() = Е
/
= Е
/
![]() , т. е. в
, т. е. в
![]() раз меньше,
чем в вакууме, ряд формул, описывающих
взаимодействие зарядов в диэлектрике,
будут иметь другой вид:
раз меньше,
чем в вакууме, ряд формул, описывающих
взаимодействие зарядов в диэлектрике,
будут иметь другой вид:
a) закон КулонаF=![]()
![]() ,
b) напряженность поля точечного заряда
q,
окруженного диэлектриком E=
,
b) напряженность поля точечного заряда
q,
окруженного диэлектриком E=![]()
![]() ,c) потенциал
поля точечного заряда
q,
окруженного диэлектриком
,c) потенциал
поля точечного заряда
q,
окруженного диэлектриком
![]() =
=![]()
![]() ,
d) напряженность
поля заряженной плоскости, окруженной
диэлектриком E
=
,
d) напряженность
поля заряженной плоскости, окруженной
диэлектриком E
=
![]() ,
e) напряженность
поля между двумя разноименно заряженными
пластинами Е=
,
e) напряженность
поля между двумя разноименно заряженными
пластинами Е=![]() ,
f) для
заряженного цилиндра
, окруженного
диэлектриком Е
=
,
f) для
заряженного цилиндра
, окруженного
диэлектриком Е
=
![]() ,
при r
,
при r
![]() g)
для заряженного шара, окруженного
диэлектриком E
=
g)
для заряженного шара, окруженного
диэлектриком E
=
![]() , при r
, при r![]() и
т.д., всюду
вместо
и
т.д., всюду
вместо
![]() пишется
пишется
![]()
![]() .
.
