62. Уравнения Максвелла для электромагнитного поля.

В основе теории Максвелла лежат рас­смотренные четыре уравнения:

1. Электрическое поле мо­жет быть как потенциальным (e_q), так и вихревым (Е_B), поэтому напряженность суммарного поля Е=Е_Q+Е_B. Так как циркуляция вектора e_q равна нулю, а циркуляция вектора Е_B оп­ределяется выражением, то цир­куляция вектора напряженности суммар­ного поляЭто уравнение показывает, что источни­ками электрического поля могут быть не только электрические заряды, но и меняю­щиеся во времени магнитные поля.

2. Обобщенная теорема о циркуляции вектора Н: Это уравнение показывает, что магнит­ные поля могут возбуждаться либо дви­жущимися зарядами, либо переменными электрическими полями.

3. Теорема Гаусса для поля D: Если заряд распределен внутри замкнутой поверхности непрерывно с объемной плот­ностью, то формула запишется в виде

4. Теорема Гаусса для поля В: Итак,полная система уравнений Максвел­ла в интегральной форме: Величины, входящие в уравнения Мак­свелла, не являются независимыми и меж­ду ними существует следующая связь:D=₀E, В=₀Н, j=E, где ₀ и ₀ — соответственно электриче­ская и магнитная постоянные,  и  — соответственно диэлектрическая и магнит­ная проницаемости,  — удельная прово­димость вещества.

Для стационарных полей (Е=const и В=const) уравнения Максвелла при­мут вид т. е. источниками электрического поля в данном случае являются только электри­ческие заряды, источниками магнитно­го — только токи проводимости. В данном случае электрические и магнитные поля независимы друг от друга, что и позволяет изучать отдельно постоянные электриче­ское и магнитное поля.

В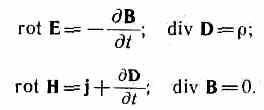оспользовавшись известными из векторного анализа теоремами Стокса и Гаусса можно представитьполную систему урав­нений Максвелла в дифференциальной форме:

Уравнения Максвелла — наиболее об­щие уравнения для электрических и маг­нитных полей в покоящихся средах. Они играют в учении об электромагнетизме такую же роль, как законы Ньютона в ме­ханике. Из уравнений Максвелла следует, что переменное магнитное поле всегда свя­зано с порождаемым им электрическим полем, а переменное электрическое поле всегда связано с порождаемым им магнит­ным, т. е. электрическое и магнитное поля неразрывно связаны друг с другом — они образуют единое электромагнитное поле.

66. Дифференциальное уравнение электромагнитной волны. Плоские электромагнитные волны.

Для однородной и изотропной среды вдали от зарядов и токов, создаю­щих электромагнитное поле, из уравнений Максвелла следует, что векторы напряженностей Е и Н переменного электро­магнитного поля удовлетворяют волново­му уравнению типа:

—оператор Лапласа.

Т.е. электро­магнитные поля могут су­ществовать в виде электромагнитных волн. Фазовая скорость электромагнитных волн определяется выражением (1) v — фазовая ско­рость, где с= 1/₀₀, ₀ и ₀ — соответственно электрическая и магнитная постоянные,  и  — соответственно электрическая и магнитная проницаемости среды.

В вакууме (при =1 и =1) скорость распространения электромагнитных волн совпадает со скоростью с. Так как > 1, то скорость распространения электро­магнитных волн в веществе всегда мень­ше, чем в вакууме.

При вычислении скорости распростра­нения электромагнитного поля по формуле (1) получается результат, достаточно хорошо совпадающий с эксперименталь­ными данными, если учитывать зависи­мость  и , от частоты. Совпадение же размерного коэффициента в со скоростью распространения света в вакуу­ме указывает на глубокую связь между электромагнитными и оптическими явле­ниями, позволившую Максвеллу создать электромагнитную теорию света, согласно которой свет представляет собой электро­магнитные волны.

Следствием теории Максвелла являет­ся поперечность электромагнитных волн: векторыЕ и Н напряженностей электриче­ского и магнитного полей волны взаимно перпендикулярны (рис. 227) и лежат в плос­кости, перпендикулярной вектору v скоро­сти распространения волны, причем векто­ры Е, Н и v образуют правовинтовую систему. Из уравнений Максвелла следует также, что в электромагнитной волне век­торы Е и Н всегда колеблются в одина­ковых фазах (см. рис. 227), причем мгно­венные значения £ и Я в любой точке связаны соотношением ₀=₀Н. (2)

Этим уравнениям удов­летворяют, в частности, плоскиемонохро­матические электромагнитные волны (электромагнитные волны одной строго определенной частоты), описываемые уравнениями Е_у=Е₀cos(t-kx+), (3) H_z=H₀cos(t-kx+), (4), где е₀ и Н₀ — соответственно амплитуды напряженностей электрического и магнит­ного полей волны,  — круговая частота волны, k=/v— волновое число, — начальные фазы колебаний в точках с ко­ординатой х=0. В уравнениях (3) и (4)  одинаково, так как колебания электрического и магнитного векторов в электромагнитной волне происходят с одинаковой фазой.