контрольная работа / Примеры решения задач - 1. Механика, молекулярная физика
.pdf
5. Найти скорость вылета снаряда массой 100 г из пружинного пистолета при выстреле вертикально вверх, если жесткость пружины 60 Н/м и сжатие равно
10 см.
Ответ: 2 м/с.
КОЛЕБАНИЯ И ВОЛНЫ
Задача 1.
Материальная точка совершает гармонические колебания с частотой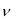 
0,5 c 1. Амплитуда колебаний
А = 80 см. Как зависит смещение x точки от времени, если колебательное движение начато из положения равновесия?
Решение.
Так как точка совершает гармонические колебания, то
x Asin( t 
0 ) Asin( 2 t 
0 ),
где 0 - начальная фаза колебаний при t = 0.
Так как по условию движение начато из положения равновесия, то
0 |
Asin( 0 |
0 ), отсюда sin 0 0, 0 0. |
Поэтому |
|
|
x |
Asin 2 |
t 0,8sin t м. |
|
|
Задача 2. |
Два математических маятника, длины которых отличаются на 22 см, совершают за некоторое время один N1 30 колебаний, второй - N2 36 колебаний.
Найти длины маятников.
Решение.
Период колебаний математического маятника определяется формулой:
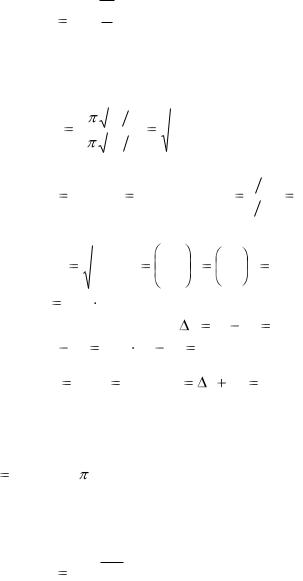
T 2
g ,
где - длина нити, g – ускорение свободного падения. Очевидно, что маятник большей длины совер-
шает за определенное время меньшее число колебаний:
|
T1 |
|
2 |
|
|
|
1 |
|
g |
|
|
|
1 |
|
. |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
T2 |
2 |
|
|
|
2 |
g |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
С другой стороны |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
T |
|
|
|
t |
, T |
|
|
|
|
|
t |
, |
|
|
тогда |
T1 |
|
|
t N1 |
|
N2 |
. |
||||||||||||||
1 |
|
|
N1 |
2 |
|
|
|
N2 |
|
|
|
|
|
|
|
T2 |
|
|
t N2 |
|
N1 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
N2 |
|
|
|
|
|
|
, |
|
|
|
N2 |
|
36 |
|
1,44, |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
N1 |
|
|
|
|
|
2 |
2 |
N1 |
30 |
|
|
|
|
|
|
||||||||||||||||||||
то есть 1 |
1,44 |
|
2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
По условию задачи |
1 |
|
2 |
0,22 м, |
||||||||||||||||||||||||||||||||
1 |
2 |
1,44 |
|
2 |
2 |
0,22. |
|
|
|
|
|
|
||||||||||||||||||||||||
2 |
0,22 |
|
|
|
|
0,5 м, 1 |
|
2 |
|
0,72 м. |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
0,44 |
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Задача 3.
Разность потенциалов на обкладках конденсатора в колебательном контуре изменяется по закону
U 50cos(104 t). Емкость конденсатора 9·10-7 Ф. Найти
индуктивность контура, а также длину волны, соответствующую этому контуру.
Решение. Из формулы Томсона
T 2
LC
найдем |
|
L |
|
|
T 2 |
|
|
, |
или, |
учитывая, что |
T |
2 |
, |
||||||
|
|
|
4 2C |
|
|||||||||||||||
L |
1 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
C |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Из U |
50 cos104 |
t видно, что |
104 |
рад с , следова- |
|||||||||||||||
тельно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
1 |
|
|
|
|
1,12 10 3 |
Гн. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
9 10 |
|
7 Ф (104 |
рад с)2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
Длина волны равна |
|
cT , |
где с – скорость |
||||||||||||||
света. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cT |
|
2 c |
|
2 3 108 |
м с |
|
6 104 м. |
|
|
||||||
|
|
|
|
|
|
|
104 |
рад с |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ 5. 1. Уравнение гармонических колебаний
x 0,04cos t . Найти амплитуду, период, частоту, на-
чальную фазу. Определить смещение точки через 0,5 с.
Ответ: 0,04 м; 2 с; 0,5 с-1; 0 рад; 0 м.
2. Через сколько времени после начала движения точка, совершающая колебательное движение по закону x 7 sin 0,5 t, проходит путь от положения рав-
новесия до максимального смещения?
Ответ: через 1 с. 3. Груз массой 200 г, подвешенный к пружине, совершает 30 колебаний за одну минуту. Определить
жесткость пружины.
Ответ: 2 Н/м. 4. Шарик подвешен на нити длиной 1 м к потолку вагона. При какой скорости вагона шарик будет
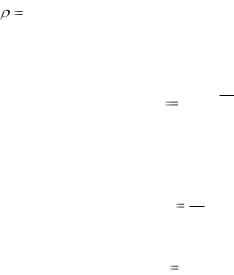
особенно сильно колебаться под действием ударов колес о стыки рельсов? Длина рельса 12, 5 м.
Ответ: 6,3 м/с. 5. Какую индуктивность надо включить в колебательный контур, чтобы при емкости 2 мкФ получить звуковую частоту 103 Гц? Сопротивлением контура пре-
небречь.
Ответ: 0,0397 Гн.
ОСНОВЫ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ.
УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА.
Задача 1.
Найти значение средней кинетической энергии поступательного движения одной молекулы гелия, имеющего при давлении Р = 100 кПа плотность
0,12кг / м3 .
Решение.
Воспользуемся основным уравнением молеку- лярно-кинетической теории газов:
Р |
2 nEк , |
||
|
3 |
||
где Р ─ давление газа, |
|
|
к ─ средняя кинетическая |
Е |
|||
энергия поступательного движения одной молекулы. Число молекул в единице объема:
nN V
N ─ число всех молекул газа определяется по формуле:
N |
m |
N A , |
|
M |
|||
|
|
где N A ─ число Авогадро ( N A |
|
6.02 10231/ моль ); |
|||||||||||||||||||||||
|
|
M – молярная масса газа ( M |
4 10 3 |
|
кг / моль ); |
||||||||||||||||||||
|
|
m |
─ |
масса |
|
газа |
, |
|
ее можно определить |
||||||||||||||||
m |
|
V .Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
n |
N |
|
|
m N A |
|
|
N A |
. |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
V |
|
|
M V |
|
|
|
M |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Следовательно, |
|
|
|
|
|
3 P |
3 |
|
P M |
. |
|
||||||||||||||
Ek |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 n |
2 N A |
|
|
|
|
|
|||||||
Подставляя числовые значения, получим: |
|
|
|||||||||||||||||||||||
|
|
|
3 |
|
|
100 103 Па 4 10 3 кг / моль |
|
8,3 10 21 Дж |
|||||||||||||||||
E |
|
|
|
|
|||||||||||||||||||||
K |
2 |
|
6,02 1023 1/ моль 0,12кг / м3 |
||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача 2. |
|
|
|
|
|
||||||||
|
|
|
|
В одном баллоне емкостью V1 = 2 л давление |
|||||||||||||||||||||
газа P |
|
33 кПа , в другом, |
емкостью V |
2 |
|
= 6 л, давление |
|||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
того же газа P2 |
|
66 кПа . Баллоны соединяют трубкой, |
|||||||||||||||||||||||
имеющий кран. Какое давление становится в баллонах при открывании крана? Процесс считать изотермическим.
Решение.
После того как откроем кран, каждый газ заполнит весь объем сосудов V = V1 + V2 . При этом в них установится давление на основании закона Дальтона
P P1' P2' ,
где P1 и Р2 ─ парциальные давления первого и второго газа соответственно после заполнения всего объема V.
По закону БойляМариотта уравнение состояния для первого газа запишется
|
|
PV |
P' (V |
V ) |
, откуда P |
' |
|
P1V1 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
1 |
1 |
|
1 |
1 |
|
2 |
|
|
1 |
|
V1 |
V2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
для второго газа |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
P V |
|
|
|
P' (V |
V ) |
, откуда P' |
|
|
P2V2 |
. |
|
||||||
|
|
2 |
|
|
|
|
|
||||||||||||
|
|
2 |
|
2 |
1 |
|
2 |
|
|
2 |
|
V1 |
V2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Следовательно, |
|
давление |
в |
|
|
сосудах |
будет |
||||||||||||
P |
P1V1 |
P2V2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
V1 |
V2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Подставим числовые значения и получим |
|
|
|
|
|||||||||||||||
|
|
P |
|
33кПа |
2л |
66кПа 6л |
57,75 кПА . |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
2л |
6л |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Задача 3.
Из баллона со сжатым водородом емкостью V = 10 л вследствие неисправности вентиля утекает газ. При
температуре |
t 70 C |
манометр |
оказывает |
|
1 |
|
|
P 5 106 Па .Через некоторое время при температуре t2 170 C манометр показывает такое же давление. Сколько газа утекло? Универсальная газовая постоянная
Дж
R = 8,31 моль 
К .
Решение.
Запишем уравнение Менделеева – Клапейрона для двух состояний газа при температурах Т1 и Т2
|
PV |
m1 |
RT |
PV |
m2 |
RT |
|
|
|
|
2 , |
||||
|
|
M |
1 И |
|
M |
||
|
|
|
|
|
|||
где m1 |
─ масса газа была в баллоне при температуре T1 , |
||||||
m2 |
─ масса газа стала в баллоне при температуре |
||||||
T2 . |
|
|
|
|
|
|
|
Утекло газа m |
m1 m2 . |
|
|
|
|
||
Выразим m1 и m2 из уравнений состояний и найдем m .
|
m |
|
|
PVM |
, |
m |
|
|
PVM |
. |
|
|
|
|
|
|
|
|
||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||
1 |
|
|
RT1 |
|
|
|
|
RT2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
m |
m |
m = |
PVM |
( |
1 |
|
1 |
) . |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
1 |
|
2 |
|
|
R |
|
|
T1 |
T2 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Подставим числовые значения, выразив все величины в |
|
|||||||||||||||||||||||||
системе единиц СИ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
T1 = t1 + 273 = 280 К, T2 = t2 + 273 = 290 К, |
|
|
|
|
|||||||||||||||||||||
|
|
V |
10 10 3 м3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
5 106 Па 10 10 3 |
м3 |
2 10 |
3 |
|
кг |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
m |
|
|
|
моль |
( |
1 |
1 |
) |
1 |
|
1,5 10 3 кг |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
Дж |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
8,31 |
|
|
|
|
|
|
|
|
|
|
280 |
290 |
|
К |
|
|||||||||||
моль К |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Задача 4.
Цилиндрическую стеклянную трубку, открытую с обеих сторон, погружают до половины в ртуть. Затем закрывают верхнее отверстие трубки и вынимают ее из ртути. При этом в трубке остается столбик ртути длиной1 = 24 см. Чему равно атмосферное давление, если
длина трубки = 90 см? Решение.
До закрывания отверстия воздух над ртутью занимает
объем V 2 
S ,
где S – площадь поперечного сечения трубки.
Воздух находится под давлением, равным атмосферному:
P1 PАТ
1
После того, как закрыли верхнее отверстие и трубку вынули из ртути, объем воздуха над ртутью стал
V2 |
( |
1 )S , |
а его давление |
P2 |
PАТ g 1 , |
где g 1 ─ давление, создаваемое столбиком ртути высотой 1 , 
─ плотность ртути.
При постоянной температуре по закону Бойля ─ Мариотта
PV |
P V |
, или |
P |
|
|
S (P |
g |
|
) ( |
|
|
)S . |
||||
|
|
|
|
|||||||||||||
1 1 |
|
2 2 |
|
|
|
AT |
2 |
AT |
|
1 |
|
|
1 |
|
||
Сократим на S и подставим числовые значения |
||||||||||||||||
P |
0,90 |
|
(Р |
|
|
0,24 13,6 103 |
10)(0,90 |
0,24) |
||||||||
|
|
|
АТ |
|
||||||||||||
|
|
|
|
|||||||||||||
AT |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,45Р |
АТ |
0,66Р |
АТ |
0,66 0,24 13,6 103 10 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
0,21Р |
АТ |
21,1 103 , |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
откуда P |
|
105 |
Па |
|
|
|
|
|
|
|||||
|
|
|
|
|
AT |
|
|
|
|
|
|
|
|
|
|
|
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ 1. Каково давление азота, если средняя квадра-
тичная скорость его молекул 
350м / с , а его плотность 
1,2 кг / м3 ?
Ответ: Р 49 103 Па . 2. При каком давлении находится газ в баллоне емкостью V 10 л , если полная кинетическая энергия
его молекул составляет Е = 3 кДж?
Ответ: Р = 200 кПа.
3.Определить плотность азота при температуре
Т= 280 К и давлении P 3,32 106 Па . Молярная масса
азота M 28 10 3 кг / моль .
Ответ: |
40 кг / м3 . |
4. В баллоне объемом V1=0,03 м3 находится газ
под давлением P 2,5 106 |
Па при температуре Т1 = 750 |
1 |
|
К. Какой объем V занимал бы газ при нормальных усло-
виях: Т0 = 273 К, Р0 = 105 Па?
Ответ:V = 0,273 м3.
5. На какой глубине Н в воде давление в 5 раз больше атмосферного Р= 750 мм рт. ст.? Плотность
воды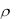 
103 кг / м3 .
Ответ: Н = 40,8 м.
6. На сколько изменилось давление воздуха в баллоне емкостью V = 50 л, если из него откачали
m 1 кг газа? Температура газа t = 27 0 C осталась по-
стоянной, его молярная масса M 29 10 3 |
кг / моль . |
Ответ: P |
1,7 105 Па . |
ТЕРМОДИНАМИКА. УРАВНЕНИЕ ТЕПЛОВОГО БАЛАНСА.
Задача 1.
Идеальный одноатомный газ совершает процесс при постоянном объеме так, что давление газа увеличи-
вается с |
P |
105 Па до |
P 5 105 |
Па. Изменение внут- |
|
1 |
|
2 |
|
ренней энергии газа при этом U |
5 103 Дж. Опреде- |
|||
лить объем газа.
Решение.
Внутренняя энергия одноатомного газа определяется по формуле
U3 m RT .
2 M
Используя уравнение Менделеева─Клапейрона
PV |
m |
RT , |
получим формулу для внутренней энер- |
||||||||||||||
|
|||||||||||||||||
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
гии: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
|
3 |
PV . |
|
|
|
|||
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
При постоянном объеме и при давлении Р1 |
||||||||||||||||
внутренняя энергия равна U |
|
|
3 2VP , а при давлении |
||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
Р2 ─ равна U |
2 |
|
3 2VP . |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
Изменение энергии равно: |
|
|
|
|
||||||||||||
|
|
|
|
U |
|
U |
|
U |
|
3 |
V (P |
P ), откуда |
|
|
|||
|
|
|
|
|
2 |
1 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
2 |
|
2 |
1 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
V |
|
2 U |
|
|
|
2 5 103 |
Дж |
8,3 10 |
3 |
м3. |
||||||
|
3 (P P ) 3 (5 105 105 ) Па |
|
|||||||||||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
Задача 2.
Какое количество теплоты выделяется при изобарном охлаждении m = 1 кг гелия от температуры t1 =
200 |
0 C до температуры t =27 0 C , молярная масса |
||
M |
4 10 3 кг / моль , универсальная газовая постоянная |
||
R |
8,31 |
Дж |
|
|
. |
||
моль К |
|||
Решение.
Согласно первому закону термодинамики количество теплоты, сообщенное системе, расходуется на изменение внутренней энергии системы и совершение работы против внешних сил.
Q 
U A .
При охлаждении газа на Т система отдает тепла столько, сколько необходимо ей при нагревании на Т. Гелий является одноатомным газом, поэтому его