контрольная работа / Примеры решения задач - 1. Механика, молекулярная физика
.pdf
На |
поверхности Земли |
|
g0 |
G |
M |
, откуда |
|||||||||||
R2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
GM g0 R2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g |
R2 |
|
g |
0 |
|
|
|
|
|
|
|
|
|
|||
g |
0 |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|||
(4R)2 |
16 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
Таким образом, сила тяжести |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
9,8 |
м |
|
|
|
|||
|
|
|
|
g0 |
|
|
|
|
|
|
|
||||||
F |
mg m |
10 кг |
с2 |
6,125 Н . |
|||||||||||||
16 |
|
|
16 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Человек массой 70 кг поднимается в лифте, движущемся вертикально вверх с постоянным ускорением 1 м/с2. Определить силу давления человека на пол кабины.
Ответ: 770 Н. 2. Два бруска массами 0,2 и 0,3 кг связаны легкой нитью и лежат на гладком столе. К более тяжелому
бруску приложена сила 1 Н, направленная параллельно плоскости стола. С каким ускорением будет двигаться
система? Определить натяжение нити.
Ответ: 2 м/с2; 0,4 Н. 3. Определить ускорение движущегося под действием силы тяжести по наклонной плоскости тела, если
коэффициент трения 0,3, а угол наклона плоскости составляет 30˚.
Ответ: 2,4 м/с2. 4. Брусок массой 1 кг движется по горизонтальной плоскости равномерно под действием силы 1 Н,
приложенной под углом 60º к плоскости. Определить коэффициент трения между бруском и плоскостью.
Ответ: 0,55. 5. Земля движется вокруг Солнца по орбите, которую можно считать круговой, радиусом 150 млн км.
Найти скорость Земли на орбите, если масса Солнца
21·1030 кг.
Ответ: 3·104 м/с.
ЗАКОНЫ СОХРАНЕНИЯ В МЕХАНИКЕ
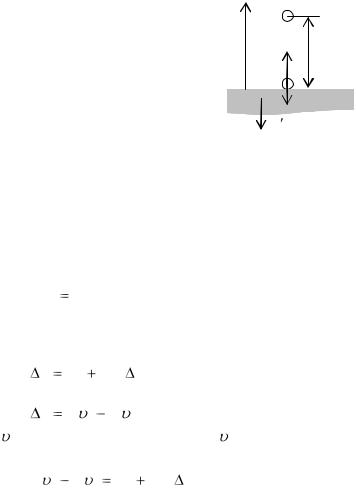
Задача 1. |
|
Y |
|
|
Стальной |
шарик |
массой |
|
|
0,05 кг падает с |
высоты |
5 м на |
h |
|
|
|
|
||
стальную плиту. После столкнове- |
F |
|||
|
|
|||
ния шарик отскакивает от плиты с |
|
|
||
такой же по модулю скоростью. |
|
mg |
||
|
||||
Найти силу, действующую на пли- |
|
|||
F |
|
|||
ту при ударе, считая ее постоян- |
|
|
||
ной. Время соударения 0,01 с. |
|
|
||
|
|
Решение. |
|
|
При ударе шар и плита действуют друг на друга с силами, равными по модулю, но противоположными по направлению по третьему закону Ньютона.
|
На шарик действуют две силы: сила тяжести |
|
|
mg |
и сила F , действующая со стороны плиты. С такой |
же силой F 
F шар действует на плиту. Согласно второму закону Ньютона, изменение импульса тела равно импульсу приложенной к нему силы и имеет такое же направление, как и сила:
|
|
|
|
|
t. |
|
p |
|
(F |
|
mg) |
|
|
Изменение импульса шарика |
||||||
|
|
|
|
, |
|
|
p |
|
m |
2 |
m 1 |
2 – скорость после |
|
где 1 – скорость шара до удара, |
||||||
удара. |
|
|
|
|
|
|
|
|
|
||||
m |
2 |
m |
1 |
(F |
mg) t. |
|
В проекции на ось Y это уравнение запишется так: m 2 ( m 1) (F mg) t.
Учитывая, что 1 2 , получим
2m F t mg t,
F mg 2mt .
Модуль скорости шарика при падении с высоты h определим из закона сохранения энергии. В верхней точке на высоте h тело обладает потенциальной энергией Ep mgh . В момент удара о плиту шарик обладает
кинетической энергией E |
m 2 |
2 . |
|
|
|
|||||||||
|
|
|
|
|
к |
|
|
|
|
|
|
|
||
mgh |
m |
2 |
, откуда |
|
|
|
|
|
|
|
||||
|
|
|
|
2gh. |
|
|||||||||
|
|
|
|
|
|
|||||||||
2 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найдем модуль силы F: |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F mg |
2m 2gh |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
t |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2 0,05 кг |
2 10 |
м |
5 м |
|
|||||||
|
|
|
|
|
|
|||||||||
0,5 Н |
с2 |
0,5 Н 100 Н 100,5 Н. |
||||||||||||
|
|
|
|
|
0,01 с |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По третьему закону Ньютона F |
F , следова- |
|||||||||||||
тельно, сила F 
, приложенная к плите, равна 100,5 Н и направлена вниз.
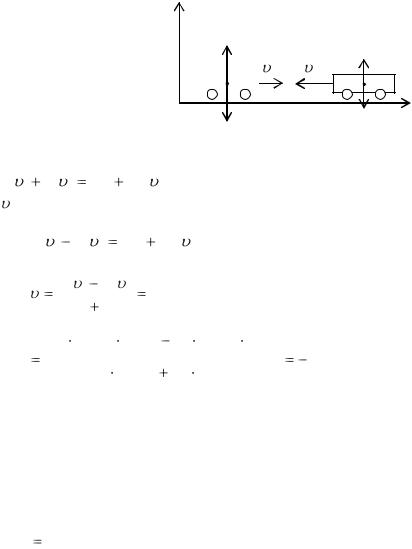
Задача 2.
Две железнодорожные платформы массами m1 = 2,4·104 кг и m2 = 1,6·104 кг двигались навстречу друг
другу со |
скоростями, модули которых равны |
|||
1 |
0,5 м с |
и |
2 |
1,0 м с. Найти скорость их совмест- |
|
|
|
||
ного движения после того, как сработала сцепка.
|
|
|
|
|
|
|
|
Решение. |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||||
|
|
Внешние силы |
N1 |
и m1g , |
N 2 и |
m2 g |
, |
||||||
вующие на тела системы, |
Y |
|
|
|
|
||||||||
взаимно |
уравновешивают- |
|
|
|
|
||||||||
|
|
|
|
|
|
||||||||
ся. |
Проекции указанных |
|
|
|
|
|
|||||||
сил на направление X рав- |
|
|
N1 |
|
|
||||||||
ны нулю, поэтому проек- |
|
|
|
|
|
||||||||
|
|
|
1 |
|
2 |
||||||||
цию импульсов системы на |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
||||||||
это |
|
направление |
можно |
|
|
|
|
|
|||||
считать постоянной. |
|
|
|
|
m1g |
|
|
||||||
|
|
По |
закону сохране- |
|
|
|
|
|
|
||||
ния импульса имеем: |
|
|
|
|
|
|
|
||||||
|
m |
|
m |
|
(m |
m ) |
, |
|
|
|
|
|
|
|
1 |
1 |
2 |
2 |
1 |
2 |
|
|
|
|
|
|
|
где |
|
— скорость платформ после сцепки. |
|
|
|||||||||
|
|
В проекции на ось X имеем: |
|
|
|
|
|||||||
|
|
m1 1 |
|
m2 2 |
(m1 |
m2 ) . |
|
|
|
|
|||
дейст-
N 2
m2 g X
Откуда
|
m1 1 |
m2 |
2 |
|
|
|
|
|
|
|
|
|
|
m1 |
m2 |
|
|
|
|
|
|
|
|
|
|
2,4 104 |
кг |
0,5 |
м |
1,6 104 |
кг 1,0 |
м |
|
|
|
|
||
с |
с |
|
|
м |
||||||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
0,1 |
|
. |
||
|
2,4 104 кг |
1,6 104 |
кг |
|
|
с |
||||||
Знак «минус» показывает, что скорость платформ после сцепки направлена противоположно оси X.
Задача 3.
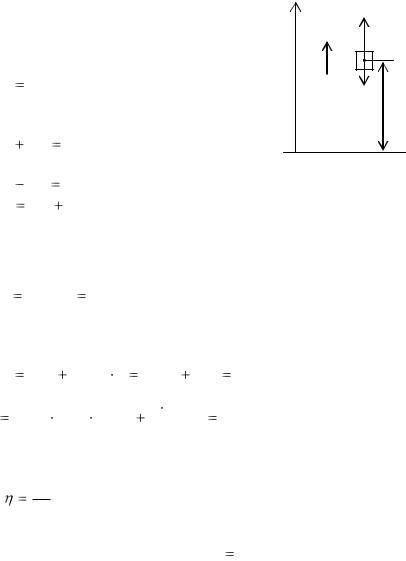
Какую работу нужно совершить, чтобы поднять равноускоренно груз массой 30 кг на высоту h = 10 м за 5 с? Какой мощности двигатель надо поставить для этого подъема, если коэффициент полезного действия установки 
80% ?
Решение.
На тело действуют сила тяжести mg и
сила F , необходимая для подъема груза. Величина работы определяется по
формуле:
A F 
h .
По второму закону Ньютона при равноускоренном движении
|
|
|
F |
mg |
ma. |
Y
F
a
mg
h
В проекции на ось Y уравнение примет вид: F mg ma, откуда
F mg ma.
Величину ускорения найдем из формулы пути при равноускоренной движении с нулевой начальной скоростью:
|
at 2 |
2h |
||
h |
|
; a |
|
. |
2 |
t 2 |
|||
После подстановки силы в формулу для работы получим:
A (mg m |
2h |
) h mh(g |
2h |
) |
||||
|
|
|
||||||
t 2 |
|
t 2 |
||||||
30 кг 10 м (10 |
м |
|
2 10 м |
) |
3240 Дж. |
|||
|
|
|
|
|||||
с2 |
|
25 с2 |
|
|||||
Коэффициент полезного действия двигателя равен отношению полезной работы Ап к затраченной Аз:
Aп .
Аз
Полезная работа расходуется на подъем груза на высоту h. Затраченная работа равна Aз N 
t, где N — мощность двигателя.
Aп , откуда
N t
N |
Aп |
|
3240 Дж |
810 Вт. |
t |
|
0,8 5 с |
||
|
|
|
Задача 4.
Пуля массой m = 10 г, летящая со скоростью 0 800 м
с , пробила доску толщиной S = 8 см. После
этого скорость пули уменьшилась до 
400 м
с. Найти
среднюю силу сопротивления, с которой доска действует на пулю.
Решение.
Работа силы сопротивления доски равна изменению кинетической энергии пули:
A E2 E1.
Кинетическая энергия в каждом случае
|
|
m |
2 |
|
|
|
|
m |
2 |
|
|
|
|
|
|
|
E |
|
|
0 |
, E |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||
1 |
2 |
|
|
|
2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Работа |
|
силы, |
|
по |
определению, |
равна |
||||||||||
A FS cos |
. Учтем, |
что сила сопротивления направле- |
||||||||||||||
на противоположно перемещению, |
|
|
180 , cos |
1 , |
||||||||||||
и работа A |
|
FS. Тогда |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
m 2 |
|
m |
2 |
|
|
m |
2 |
|
m 2 |
|
|||
FS |
|
|
|
|
|
0 |
или |
|
0 |
|
|
FS, |
|
|||
2 |
|
2 |
2 |
|
2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||
то есть уменьшение механической энергии пули равно работе по преодолению силы сопротивления доски.
|
|
m( |
2 |
2 ) |
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2S |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
0,01 кг |
(800 |
2 |
|
м2 |
|
400 |
2 м2 |
) |
|
|
|
||||
|
|
|
|
с2 |
|
|
с2 |
3 10 |
4 |
Н. |
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
2 |
|
|
0,08 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
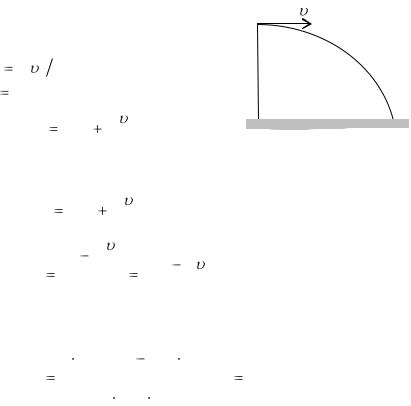
Задача 5.
С какой высоты брошено горизонтально со скоростью 10 м/с тело массой 2 кг, если его кинетическая энергия в момент удара о землю составила Ек = 300 Дж? Сопротивлением воздуха пренебречь.
Решение.
Решим задачу, используя закон сохранения энергии.
В момент удара о землю (в точке В) тело обладает только кинетической энергией Ек, так как на этом уровне потенциальная энергия те-
ла равна нулю. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
|||||
|
В точке А тело обладает |
|
||||||||||||||||||
|
|
|
||||||||||||||||||
как |
кинетической |
|
|
|
энергией |
|
|
|||||||||||||
Eк 0 |
m 2 |
2 , так и потенциальной h |
||||||||||||||||||
Ep |
mgh , т.е. полная энергия |
|
|
|
|
|
||||||||||||||
|
E |
|
mgh |
|
m 2 |
|
. |
|
|
|
|
|
|
|
В |
|||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||
|
Следовательно, по закону сохранения энергии |
|||||||||||||||||||
можем написать: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Eк |
|
mgh |
|
|
m |
2 |
, |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
2 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Eк |
m 2 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
2Eк |
m |
2 |
|
|
|
|||
|
h |
|
2 |
|
|
|
|
|
. |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
mg |
|
|
|
|
|
|
|
|
2mg |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
После подстановки числовых значений полу- |
|||||||||||||||||||
чим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 300 Дж |
|
|
|
2 кг 100 |
|
м2 |
|
|
|||||||||
|
h |
|
|
|
|
|
с2 |
|
10 м. |
|||||||||||
|
|
|
|
2 2 кг 10 |
м |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
с2 |
|
|
|
|
|
||||||||||
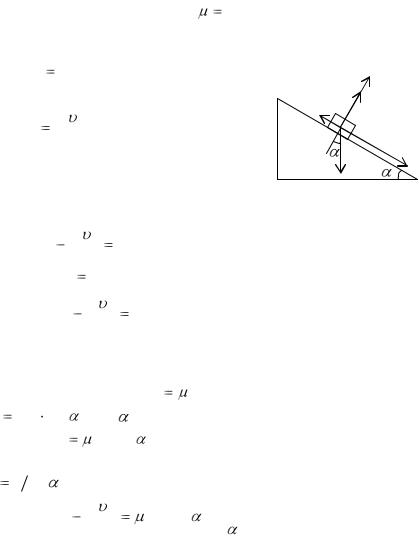
Задача 6.
С наклонной плоскости высотой 5 м скользит тело. Его начальная скорость равна нулю, а скорость у основания плоскости 6 м/с. Найти угол наклона плоско-
сти, если коэффициент трения |
0,27. |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Решение. |
|
|
|
|
|||
|
На высоте h тело обладает потенциальной энер- |
|||||||||||||||||
гией E р |
mgh ; у основания в точке |
|
|
|
Y |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
С тело обладает кинетической энер- |
|
А |
|
|||||||||||||||
|
Fтр |
|||||||||||||||||
|
|
m |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
N |
||
гией Eк |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2 |
|
|
|
|
|
механической |
|
h |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Уменьшение |
|
|
|
||||||||||||||
энергии тела равно работе по пре- |
|
|
|
mg |
||||||||||||||
|
|
|
|
|||||||||||||||
одолению силы трения на участке |
|
O |
|
|
||||||||||||||
пути АС: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mgh |
|
m 2 |
|
|
Aтр , |
|
|
|
|
|
|
|
|||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
где Aтр |
|
|
Fmp S, |
|
|
|
|
|
|
|
|
||||||
|
mgh |
|
|
m 2 |
|
Fmp S. |
|
|
|
|
|
|
|
|||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
На тело действуют следующие силы: сила тяже- |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сти mg , сила реакции опоры N , сила трения Fmp. |
|
|||||||||||||||||
|
Сила трения |
Fmp |
N. |
Из рисунка видно, что |
||||||||||||||
N |
mg cos |
, где |
- угол наклона плоскости. Тогда |
|||||||||||||||
|
Fmp |
|
|
mg cos . |
|
|
|
|
|
|
|
|||||||
|
Путь |
|
|
S |
|
|
выразим |
их треугольника |
АОС: |
|||||||||
S |
h sin |
, тогда |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
mgh |
|
|
m |
2 |
|
|
mg cos |
h |
. |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
2 |
|
|
|
sin |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
X
С
Сократим на массу m, тогда
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
gh |
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
ctg |
2 |
|
|
|
|
|
, |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
gh |
|
|
|
|
2 |
gh |
|||||||
|
|
36 |
м2 |
|
|
|
|
|
|
|
|
|
|||||||
|
1 |
с |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ctg |
|
|
|
|
|
|
|
|
|
|
|
|
|
2,4. |
23 . |
||||
0,27 |
2 0,27 10 |
|
м |
|
5 м |
||||||||||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
с2 |
|
|
|
|
|
|||||||||||
Задача 7.
На нити висит шарик массой 0,1 кг. Шарик отклонили от положения равновесия на угол 
90
и отпустили.
Какова сила натяжения нити при прохождении шариком положения равновесия?
Решение.
При прохождении шариком вертикального по-
ложения на него действуют сила тяжести mg и сила на-
тяжения нити T . Эти силы сообщают телу центростре-
мительное (нормальное) ускорение an , направленное
вертикально вверх. |
|
|
|
|
|
|
|
|
||
По второму закону Ньютона |
Y |
|
|
A |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
||||
T |
mg |
man , |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
или в проекции на ось Y: |
|
|
|
|
|
|||||
T |
mg |
ma , |
где a |
2 |
. |
|
|
an |
|
|
|
|
|
|
|
||||||
|
|
n |
|
n |
|
|
|
B E p |
0 |
|
Следовательно, |
|
|
|
|
|
|||||
|
|
|
|
mg |
|
|
|
|||
2
T mg m .
Применим закон сохранения энергии, считая что в точке А тело обладает только потенциальной энергией
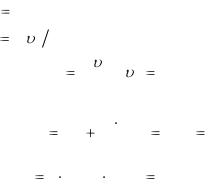
Ep |
mg , а |
в |
точке |
В — только кинетической |
||
E |
m 2 2. По закону сохранения энергии |
|||||
к |
|
|
|
|
|
|
|
mg |
m |
2 |
; |
2 |
2g . |
|
2 |
|
|
|||
Уравнение для Т приобретет тогда вид:
T |
mg |
|
m 2g |
3mg |
||
|
|
|||||
|
|
|
|
|||
3 |
0,1 |
кг 10 |
м |
3 Н. |
||
|
|
|||||
с2 |
||||||
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Конькобежец массой 60 кг бросает в горизонтальном направлении камень массой 2 кг со скоростью 15 м/с. На какое расстояние откатится при этом конькобежец, если известно, что коэффициент трения полозьев о лед 0,02?
Ответ: 0,64 м. 2. Ядро, летевшее горизонтально со скоростью 50 м/с, разорвалось на два осколка массами 2 и 3 кг.
Скорость большего осколка равна 30 м/с и направлена горизонтально в сторону движения ядра до разрыва. Определить значение скорости меньшего осколка.
Ответ: 80 м/с. 3. Тело массой 100 г, брошенное вертикально вверх с начальной скоростью 15 м/с, достигло макси-
мальной высоты 15 м. Определить работу сил сопротивления воздуха на этом участке.
Ответ: 6,35 Дж. 4. Тело брошено вертикально вверх. На высоте 6,4 м его кинетическая энергия равна потенциальной.
Определить начальную скорость тела.
Ответ: 16 м/с.