Контрольные вопросы:
Понятие множества и его элементов. Способы задания множеств.
Конечное и бесконечное множества.
Подмножество. Свойства подмножеств.
Операции над множествами.
Основные числовые множества.
Мощность множества. Счётное и несчётное множества.
Декартово произведение множеств.
Нечёткие множества. Пример.
Операции над нечёткими множествами.
Понятие лингвистической переменной.
Контрольные задания:
1.
Определить является ли одно из множеств
и
собственным подмножеством другого:
а)
{1,{1,2}},
{{1,2},2},
б)
{1},
{1,{1}}.
2.
Какие
из элементов множества
одновременно являются и его подмножествами:
{Ø,{Ø},{1}}?
3.
Для
двухэлементного множества
построить
- множество всех подмножеств
:
={1,2}.
4.
Найти
объединение, пересечение, разность и
декартово произведение множеств
и
:
а)
и
– множества всех букв слов «параллельность»
и «трапеция»,
б)
и
– множества всех цифр чисел 3464675678
и 3464758858.
5. Найти объединение, пересечение и разность следующих промежутков:
а) [3;7), (4;9],
б)
(-
;5],
(0;+
),
в) [1;10], (-7;4].
6. Доказать и с помощью диаграмм Эйлера-Венна проверить:
а)
\
=
\(
),
б)
\
= (
)\
,
в)
(
)\
= (
\
)
(
\
),
г)
(
\
)
(
\
)
= (
)\
.
7. Решить задачу:
Из 32 учеников класса 12 занимаются в волейбольной секции, 15 – в баскетбольной, 8 – и в той, и в другой. Сколько школьников не занимаются ни в волейбольной, ни в баскетбольной секциях.
Задания для домашней работы:
1.
Найти
объединение, пересечение, разность и
декартово произведение множеств
и
:
а)
и
– множества всех букв слов «алгебра»
и «планета»,
б)
и
– множества всех цифр чисел 5660399839
и 5382388992.
2. Доказать и с помощью диаграмм Эйлера-Венна проверить:
а)
(
\
)\
=
\(
),
б)
\(
\
)
= (
\
)
(
),
в)
(
\
)
(
\
)
= (
)\(
).
3. Найти объединение, пересечение и разность следующих промежутков:
а)
(-1;3),
[2;+
),
б) [1;4), [2;3],
в)
[1;3),
[5;
+
).
Тема №2 «Элементы математической логики»
Цель: научиться приводить дизъюнктивные и конъюнктивные нормальные формы к совершенным дизъюнктивным и конъюнктивным нормальным формам, используя логические равносильности; применять законы математической логики для решения логических задач; применять язык логики предикатов для записи математических предложений, определений, построения противоположных утверждений.
Краткие теоретические сведения:
Высказывание – любое повествовательное предложение, которому можно приписать истинностное значение.
Предложение, которое содержит хотя бы одну переменную и становится высказыванием при подстановке вместо всех переменных их значений, называется высказывательной формой.
Высказывание, представляющее собой одно утверждение, называется элементарным.
Высказывание, образованное из элементарных с помощью логических связок «и», «или», «если, то», «не», называется составным (сложным).
Образование составного высказывания из элементарных называется логической операцией.
Логическая
операция, соответствующая логической
связке «не» («неверно, что») называется
отрицанием:
.
Отрицание истинно, когда основное
высказывание ложно.
|
|
|
|
1 |
0 |
|
0 |
1 |
Логическая
операция, соответствующая логической
связке «и», называется конъюнкцией:
.
Конъюнкция истинна, когда истинны оба
высказывания.
|
|
|
|
|
0 |
0 |
0 |
|
1 |
0 |
0 |
|
0 |
1 |
0 |
|
1 |
1 |
1 |
Логическая
операция, соответствующая логической
связке «или», называется дизъюнкцией:
.
Дизъюнкция ложна, когда ложны оба
высказывания.
|
|
|
|
|
0 |
0 |
0 |
|
1 |
0 |
1 |
|
0 |
1 |
1 |
|
1 |
1 |
1 |
Логическая
операция, имеющая вид «если
,
то
»,
называется импликацией:
.
Высказывание
называется посылкой,
– заключением. Импликация ложна, когда
посылка истинна, а заключение ложно.
|
|
|
|
|
0 |
0 |
1 |
|
1 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
1 |
1 |
Логическая
операция, соответствующая сложному
союзу «тогда и только тогда, когда»,
называется эквиваленцией:
.
Эквиваленция истинна, когда оба
высказывания одновременно истинны или
одновременно ложны.
|
|
|
|
|
0 |
0 |
1 |
|
1 |
0 |
0 |
|
0 |
1 |
0 |
|
1 |
1 |
1 |
Приоритет логических операций: отрицание, конъюнкция, дизъюнкция, импликация, эквиваленция.
Под
формулой
логики высказываний понимается следующее:
всякое элементарное высказывание есть формула,
если
и
– формулы, то
,
,
,
,
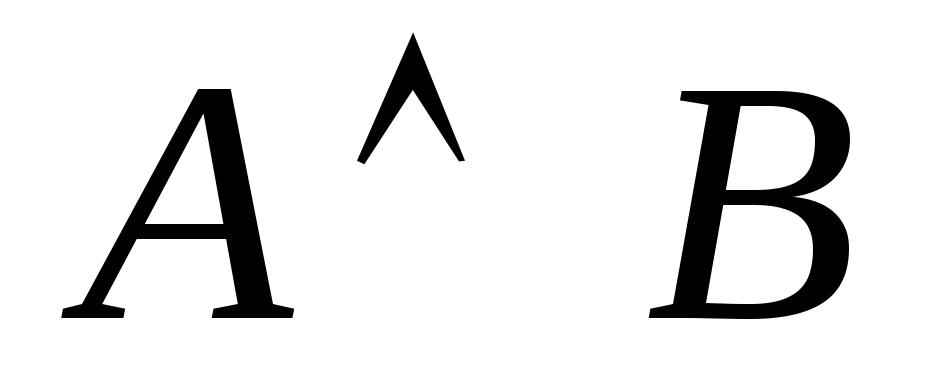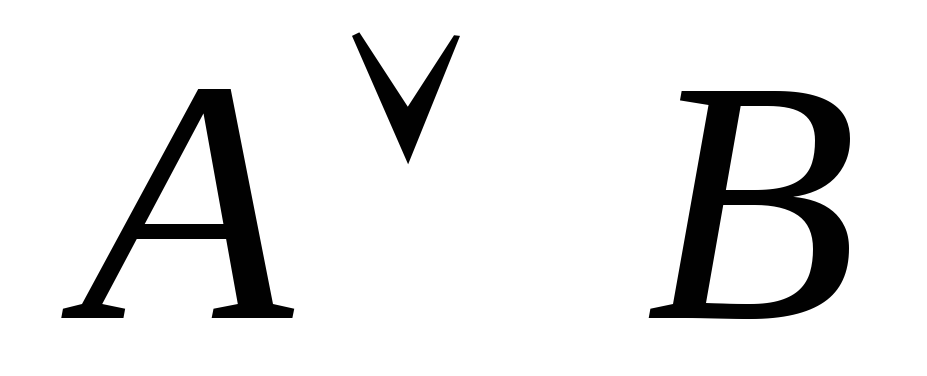,других формул, кроме перечисленных в 1) и 2), нет.
Две
формулы называются равносильными,
если их таблицы истинности совпадают:
.
Основные формулы математической логики:
1)
- закон тождества,
2)
- закон противоречия,
3)
- закон исключённого третьего,
4)
- снятие двойного отрицания,
5)
,
- идемпотентность,
6)
,
- коммутативность,
7)
,
- ассоциативность,
8)
,
- дистрибутивность,
9)
,
- законы Де Моргана,
10)
,
,
,
- сочленение переменной с константой,
11)
,
- законы поглощения,
12)
,
- законы склеивания,
13)
,
- замена импликации,
14)
- правило modus
ponens,
15)
- правило силлогизма,
16)
- закон контрапозиции,
17)
- соединение посылок,
18)
- разъединение посылок.
Примеры.
1) Доказать формулу
.
Решение.
-
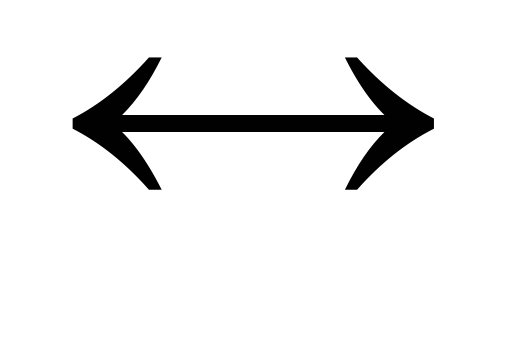
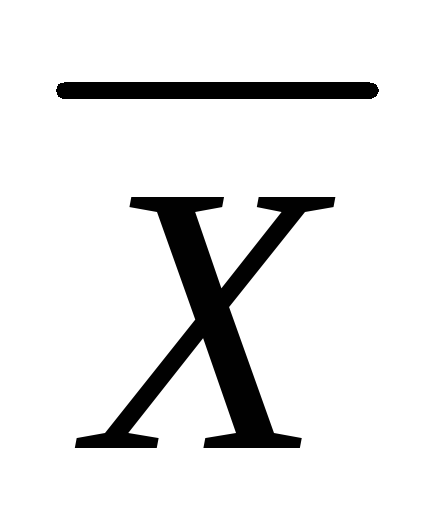
1
0
0
1
0
0
0
1
1
0
1
0
1
0
0
1
1
1
1
1
1
0
1
1
1
1
1
1
Видим, что средний столбик состоит из одних единиц, равносильность доказана.
2)
Упростить формулу
.
Решение.
.
Формула называется тождественно – истинной (тавтологией) (тождественно – ложной (противоречием)), если её истинностное значение «истина» («ложь») при любых возможных значениях переменных.
Предложение
называется прямым
утверждением,
- обратным,
- противоположным,
- обратнопротивоположным.
Если
предложение
- истинно, то оно называется теоремой.
- достаточное
условие
для
,
- необходимое
условие
для
или следствие
.
Если
- истинно и
- истинно, то
- необходимое и достаточное условие для
,
а
- необходимое и достаточное условие для
.
Дизъюнктивная нормальная форма (ДНФ) представляет собой дизъюнкцию конъюнкций переменных и их отрицаний, либо конъюнкцию самих переменных.
Конъюнктивная нормальная форма (КНФ) представляет собой конъюнкцию дизъюнкций переменных и их отрицаний, либо дизъюнкцию самих переменных.
Любую формулу можно привести к ДНФ или к КНФ.
Совершенная дизъюнктивная нормальная форма (СДНФ) – дизъюнкция конъюнкций, содержащих все исходные переменные (с отрицанием или без).
Совершенная конъюнктивная нормальная форма (СКНФ) – конъюнкция дизъюнкций, содержащих все исходные переменные (с отрицанием или без).
Пример.
Привести к ДНФ формулу
.
Решение.
.
Функция,
все значения которой принадлежат
множеству {0;
1}
называется предикатом:
,
.
Предикат
с
различными переменными называется
– местным предикатом.
Подмножество области определения предиката, состоящее из тех и только тех элементов, которым соответствует истинное значение предиката, называется областью истинности предиката.
Если область истинности предиката совпадает со всей областью определения, то предикат называется тождественно – истинным. Если же область истинности представляет собой пустое множество, то предикат называется тождественно – ложным.
Всякий
одноместный предикат
с переменной
,
принимающей значения из некоторого
непустого множества, выражает свойство,
присущее некоторым элементам этого
множества. Множество элементов, обладающих
свойством
,
называется объёмом
данного свойства. Многоместные предикаты
выражают отношения.
Кванторы:
1)
- квантор всеобщности,
2)
- квантор существования,
3)
- квантор существования единственности.