Задания для домашней работы:

1. Найти оценки генеральных средней, дисперсии и среднего квадратического отклонения, если совокупность задана таблицей распределения:

	6,76	6,78	6,80	6,82	6,84
	52	44	14	11	1

2. Вычислить несмещённые оценки параметров генеральной совокупности по выборочным данным. По желанию можно составить вариационный ряд по значениям:

71 71 69 74 75 70 78 66 69 74 81 73 74

3. Из генеральной совокупности извлечена выборка объема :

	-0,5	-0,4	-0,2	0	0,2	0,6	0,8	1	1,2	1,5
	1	2	1	1	1	1	1	1	2	1

Оценить с надежностью 0,95 математическое ожидание нормально распределённого признака генеральной совокупности с помощью доверительного интервала.

4. Найти доверительные интервалы для математического ожидания, дисперсии и среднего квадратического отклонения при доверительной вероятности 0,95, если из генеральной совокупности сделана выборка:

67 70 69 68 74 72 66 66 74 69 72 78 67

Тема №13 «Проверка статистических гипотез о равенстве дисперсий и математических ожиданий»

Цель: научиться проверять статистические гипотезы о равенстве дисперсий и математических ожиданий нормальных генеральных совокупностей.

Краткие теоретические сведения:

Статистической называют гипотезу о виде неизвестного распределения, или о параметрах известных распределений.

Нулевой (основной) называют выдвинутую гипотезу .

Конкурирующей (альтернативной) называют гипотезу , которая противоречит нулевой.

Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза.

Ошибка второго рода состоит в том, что будет принята неправильная гипотеза.

Вероятность совершить ошибку второго рода – уровень значимости .

Статистическим критерием называют случайную величину , которая служит для проверки нулевой гипотезы.

Наблюдаемым значением называют значение критерия, вычисленное по выборкам.

Критической областью называют совокупность значений критерия, при которой нулевую гипотезу отвергают.

Область принятия гипотезы – совокупность значений критерия, при котором гипотезу принимают.

Если принадлежит критической области – гипотезу отвергают, если принадлежит области принятия гипотезы – гипотезу принимают.

Критическими точками называют точки, отделяющие критическую область от области принятия гипотезы.

Критические точки ищут, исходя из требования, что при условии справедливости нулевой гипотезы, вероятность того, что критерий попадет в критическую область, была равна принятому уровню значимости.

Для каждого критерия имеются соответствующие таблицы, по которым находят критическую точку, удовлетворяющую этому требованию.

Когда найдена, вычисляют по данным выборок и, если > (правосторонняя критическая область), < (левосторонняя), <<, < (двусторонняя), то отвергается.

Сравнение двух дисперсий нормальных генеральных совокупностей:

Пусть и распространены нормально. По независимым выборкам с объемами, соответственно равными и , извлеченным из этих совокупностей, найдены исправленные выборочные дисперсии и . Требуется по исправленным дисперсиям при заданном уровне значимости проверить нулевую гипотезу .

1) выдвигаем конкурирующую гипотезу (),

2) находим ,

3) по таблице критических точек Фишера –Снедекора находим (), где , и - объём выборки, которой соответствует , - ,

4) если , то принимаем нулевую гипотезу, в противном случае – альтернативную.

Критерий Бартлетта. Сравнение нескольких дисперсий нормальных генеральных совокупностей по выборкам различного объема:

Пусть распределены нормально. Из этих совокупностей извлечены независимые выборки различных объемов . Найдены исправленные выборочные дисперсии. По уровню значимости и исправленным выборочным дисперсиям проверить гипотезу об однородности дисперсий : .

1) находим , где

,

,

2) находим по таблице критических точек ,

3) если , то принимаем нулевую гипотезу.

Критерий Кочрена. Сравнение нескольких дисперсий нормальных генеральных совокупностей по выборкам одинакового объема:

Пусть распределены нормально. Из этих совокупностей извлечены независимые выборки одинакового объёма . Найдены исправленные выборочные дисперсии, все с одинаковым числом степеней свободы . По уровню значимости и исправленным выборочным дисперсиям проверить гипотезу об однородности дисперсий : .

1) находим

2) находим по таблице критических точек Кочрена,

3) если , то принимаем нулевую гипотезу.

Сравнение двух математических ожиданий нормальных генеральных совокупностей, дисперсии которых известны:

Пусть и распределены нормально, их дисперсии известны. По выборкам объемов и найдены выборочные средние и . По средним и требуется проверить , то есть значимо или незначимо различаются средние.

1) выдвигаем конкурирующую гипотезу (), [],

2) находим ,

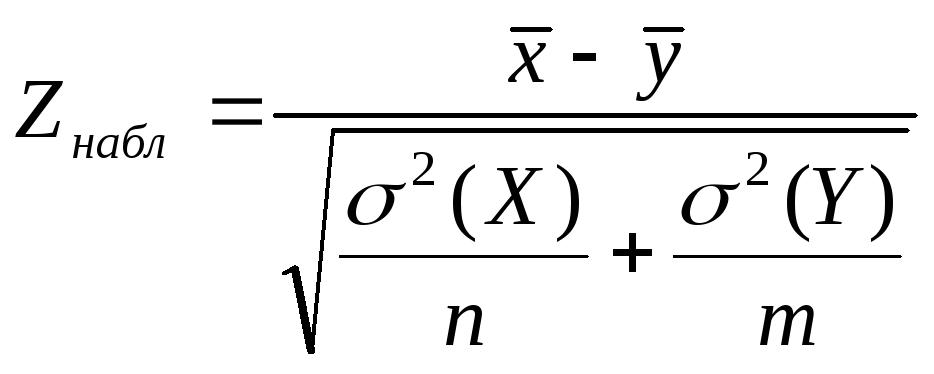3) находим из условия (), [] по таблице значений функции Лапласа и симметричную ей ,

4) если (), [], то принимаем нулевую гипотезу.

Сравнение двух математических ожиданий нормальных генеральных совокупностей, дисперсии которых неизвестны и одинаковы:

Пусть и распределены нормально, их дисперсии неизвестны. По выборкам объемов и найдены выборочные средние и и исправленные дисперсии и . По уровню значимости требуется проверить , то есть значимо или незначимо различаются средние. Предполагаем (если есть основание) дисперсии одинаковы или сравниваем их.

1) выдвигаем конкурирующую гипотезу (), [],

2) находим ,

3) находим по таблице критических точек Стьюдента и симметричную ей ,

4) если (), [], то принимаем нулевую гипотезу.