11.4. Шкалы разностей

Частным случаем интервальных шкал явля­ются шкалы разностей: циклические (периодиче­ские) шкалы, шкалы, инвариантные к сдвигу. В та­кой шкале значение не изменяется при любом числе сдвигов (рис. 11.4):

где

_{Рис.11.4. Шкала разностей}

Постоянная b называется периодом шкалы.

Примеры. В таких шкалах измеряется направление из одной точки (шка­ла компаса, роза ветров и т. д.), время суток (циферблат часов), фаза колебаний (в градусах или радианах).

Однако соглашение о хотя и произвольном, но едином для нас на­чале отсчета шкалы позволяет использовать показания в этой шкале как числа, применять к ним арифметические действия (до тех пор, пока кто-нибудь не забудет об условности нуля, например при пере­ходе на летнее время или обратно).

11.5. Шкалы отношений

Следующей по силе шкалой является шкала отношений (подо­бий). Измерения в такой шкале являются «полноправными» числа­ми, с ними можно выполнять любые арифметические действия, здесь присутствуют все атрибуты измерительных шкал: упорядоченность, интервальность, нулевая точка. Величины, измеряемые в шкале от­ношений, имеют естественный, абсолютный нуль, хотя остается сво­бода в выборе единиц (рис. 11.5):

,

где .

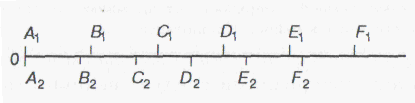
Рис.11.5. Шкала отношений

Примеры. Вес, длина, электрическое сопротивление, деньги - величины, природа которых соответствует шкале отношений.

Из значений шкалы отношений видно, во сколько раз свойство одного объекта превосходит такое же свойство другого объекта.

11.6. Абсолютная шкала

Абсолютная (метрическая) шкала имеет и абсолютный нуль (b = 0), и абсолютную единицу (а = 1). В качестве шкальных зна­чений при измерении количества объектов используются натураль­ные числа, когда объекты представлены целыми единицами, и дей­ствительные числа, если кроме целых единиц присутствуют и ча­сти объектов.

Именно такими качествами обладает числовая ось, которую есте­ственно назвать абсолютной шкалой.

Важной особенностью абсолютной шкалы по сравнению со все­ми остальными является отвлеченность (безразмерность) и абсолют­ность ее единицы. Указанная особенность позволяет производить над показаниями абсолютной шкалы такие операции, которые недо­пустимы для показаний других шкал, - употреблять эти показания в качестве показателя степени и аргумента логарифма.

Примеры.

1. Абсолютные шкалы применяются, например, для измерения количества объектов, предметов, событий, решений и т. п.

2. Примером абсолютной шкалы также является шкала температур по

Кельвину.

Числовая ось используется как измерительная шкала в явной форме при счете предметов, а как вспомогательное средство при­сутствует во всех остальных шкалах.

11.7. Шкалирование

Шкалирование представляет собой отображение какого-либо свойства объекта или явления в числовом множестве.

Можно сказать, что чем сильнее шкала, в которой производят­ся измерения, тем больше сведений об изучаемом объекте, явлении, процессе дают измерения. Поэтому так естественно стремление ка­ждого исследователя провести измерения в возможно более сильной шкале. Однако важно иметь в виду, что выбор шкалы измерения должен ориентироваться на объективные отношения, которым подчи­нена наблюдаемая величина, и лучше всего производить измерения в той шкале, которая максимально согласована с этими отношения­ми. Можно измерять и в шкале более слабой, чем согласованная (это приведет к потере части полезной информации), но применять более сильную шкалу опасно: полученные данные на самом деле не будут иметь той силы, на которую ориентируется их обработка.

Иногда же исследователи усиливают шкалы; типичный слу­чай - «оцифровка» качественных шкал: классам в номинальной или порядковой шкале присваиваются номера, с которыми дальше «работают» как с числами. Если в этой обработке не выходят за пределы допустимых преобразований, то «оцифровка» - это просто перекодировка в более удобную (например, для ЭВМ) форм; Однако применение других операций сопряжено с заблуждениями ошибками, так как свойства, навязываемые подобным образом, на самом деле не имеют места.

По мере развития соответствующей области знания тип шкалы может меняться.

Пример. Температура сначала измерялась по порядковой шкале (холод­нее - теплее), затем — по интервальным шкалам (Цельсия, Фаренгейта, Реомю­ра), а после открытия абсолютного нуля температур — по абсолютной шкале (Кельвина).

Резюме

1. В основе любого наблюдения и анализа лежат измерения, которые представляют собой алгоритмические операции: данному наблюдаемому состоянию объекта ставится в соответствие определенное обозначение: число, номер или символ. Множество таких обозначений, используемых для регистрации состояний наблюдаемого объекта, называется измерительной шкалой.

2. В зависимости от допустимых операций на измерительных шкалах их различают по их силе.

3. Самой слабой шкалой является номинальная шкала, представляющая собой конечный набор обозначений для никак не связанных между собой состояний (свойств) объекта.

4. Следующей по силе считается порядковая шкала, дающая возможность в каком-то отношении сравнивать разные классы наблю­даемых состояний объекта, выстраивая их в определенном порядке. Различают шкалы простого, слабого и частичного порядка. Числен­ные значения порядковых шкал не должны вводить в заблуждение относительно допустимости математических операций над ними.

5. Еще более сильная шкала - шкала интервалов, в которой, кроме упорядочивания обозначений, можно оценить интервал между ними и выполнять математические действия над этими интервала­ми. Разновидностью шкалы интервалов является шкала разностей, или циклическая.

6. Следующей по силе идет шкала отношений. Измерения в такой шкале являются «полноправными» числами, с ними можно выполнять любые арифметические действия (правда, при условии однотипности единиц измерения).

7. И, наконец, самая сильная шкала - абсолютная, с которой можно выполнять любые математические действия без каких-либо ограничений.

8. Отображение какого-либо свойства объекта или явления в чи­словом множестве называется шкалированием. Чем сильнее шкала, в которой производятся измерения, тем больше сведений об изучае­мом объекте, явлении, процессе дают измерения. Однако применять более сильную шкалу опасно: полученные данные на самом деле не будут иметь той силы, на которую ориентируется их обработка. Луч­ше всего производить измерения в той шкале, которая максимально согласована с объективными отношениями, которым подчинена на­блюдаемая величина. Можно измерять и в шкале, более слабой, чем согласованная, но это приведет к потере части полезной информации.