Вопрос №2 Эффективная площадь рассеяния точечных объектов.

I.3.2.1. Эпр элементарных объектов.

Элементарными считают объекты, ЭПР которых может быть достаточно просто вычислена аналитически. К ним относятся металлический лист, цилиндр, шар, уголковый отражатель, полуволновый вибратор, участок диффузно-рассеивающей поверхности, искусственные отражатели, а также некоторые групповые и распределенные цели.

Определение ЭПР таких объектов может представлять самостоятельный интерес, а также при вычислении ЭПР объектов сложной конфигурации, которые могут быть представлены совокупностью простейших объектов.

I.3.2.1.1. ЭПР участка диффузно-рассеивающей поверхности. Для нахождения ЭПР участка S хорошо проводящей выпуклой поверхности (рис. I.3.5) воспользуемся формулой (I.3.3), в которой отношение Е₂/Е₁ можно получить сумми­рованием элементарных полей, создаваемых в месте рас­положения РЛС отраженными сигналами от элементов поверхности dS.

Если расстояние от антенны РЛС до рассматриваемого элемента dS равно R и облучение происходит под углом  к нормали с напряженностью поля Е₁, то напряженность поля Е₂ в месте расположения РЛС

.

Для малоразмерных целей можно считать, что в пределах цели (поверхности S) значения R и Е_: меняются мало, поэтому

Рис. I.3.5

,

где R₀ — расстояние от РЛС до ближайшей точки поверх­ности.

Тогда

.

Поскольку .

Подставив значение в формулу (I.3.3), найдем выражение для ЭПР поверхности:

. (I.3.4)

Воспользуемся полученным выражением для вычисле­ния эффективной площади рассеяния некоторых простей­ших объектов.

I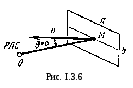.3.2.1.2. ЭПР плоской хорошо проводящей пластины. Предположим, что плоская электро­магнитная волна падает нормально на металлическую пластину с зер­кальной поверхностью, размеры которой а и b много больше _и. Мощность волны, падающей на поверхность, равна П₁S, где П₁ — плотность потока мощности падающей электромагнитной волны у пластины; S — площадь металлической пластины (рис. I.3.6).

Под действием падающей волны в пластине наводятся токи, совпадающие в любой точке пластины по фазе и амплитуде. Таким образом, поле вторичного излучения пластины будет эквивалентно полю синфазной антенны с коэффициентом направленного действия . Плотность потока мощности отраженной волны у ра­диолокационной станции.

Используя формулу (I.3.4) можно записать выражение для ЭПР металлической пластины, расположенной нормально к направлению на РЛС:

, (I.3.5)

Таким образом, при нормальном облучении идеально проводящий лист зеркально отражает всю падающую энергию в направлении РЛС, что и обеспечивает большую ЭПР по сравнению с площадью листа. При _и =10см лист площадью S= 1 м² имеет при облучении по нормали s₀= 1256 м², что в несколько раз превышает ЭПР большого самолета.

Однако даже при небольшом отклонении направления облучения от нормали ЭПР плоского листа резко падает. Предположим, что направление облучения отклонено от нормали в горизонтальной плоскости на угол  = . Рассматривая лист как плоскую синфазную антенну с диа­граммой направленности, описываемой функцией , выражение для ЭПР можно записать в виде

, (I.3.5)

где .

Зависимость ЭПР от угла облучения называют диа­граммой рассеяния цели.

Плоский лист имеет диаграмму рассеяния, описывае­мую функцией вида .

При больших отношениях размера листа к длине волны (в рассмотренном случае ) диаграмма рассеяния будет очень острой, т. е. при увеличении  значение ЭПР листа резко меняется в соответствии с функцией , снижаясь в некоторых направлениях до нуля.

Содержание

I.3.2.1.3. ЭПР уголкового отражателя (искусственный отражатель).Для ряда применений желательно сохранение большого значения ЭПР в широком диапазоне изменения углов облучения. Это необходимо, например, при использовании отражателей в качестве пассивных радиомаяков. Таким свойством обладает уголковый отражатель. Уголковый отражатель состоит из трех взаимно перпендикулярных металлических листов, он обладает свойством отражения радиоволн в сторону облучающей РЛС, что объясняется трехкратным отражением от стенок отражателя (рис. I.3.7), которое испытывает волна, если направление облучения находится вблизи оси симметрии (в пределах телесного угла 45°) уголкового отражателя.

Рис. I.3.7

Из рис. I.3.7 можно видеть, что трехкратное отражение происходит, если падающий луч проходит в пределах шестиугольника, вписанного во внешний контур отражателя. Следовательно, ЭПР уголко­вого отражателя примерно равна ЭПР плоского листа в виде такого шестиугольника, облучаемого по нормали. Подставив выражение для площади шестиугольникав (I.3.5), получим формулу для расчетаЭПР уголкового отражателя:

. (I.3.6)

При а = 1 м и _и= 10см ЭПР уголкового отражателя s_уо = 419 м². Таким образом, ЭПР уголкового отражателя несколько меньше ЭПР плоской пластины с размерами а = b = 1 м. Однако уголковый отражатель сохраняет боль­шое значение ЭПР в достаточно широком секторе, тогда как ЭПР пластины резко уменьшается при незначительных отклонениях направления облучения от нормали. Необхо­димо подчеркнуть, что достижение теоретического значения s_уо возможно лишь при высокой точности его изготовле­ния, особенно при работе на волнах короче 3 см. Для расширения действующего сектора применяют уголковые отражатели, состоящие из четырех уголков.

Вкачестве пассивных радиолокационных маяков на море используют также биконические отражатели (рис.I.3.8), составленные из двух одинаковых металлических конусов.

Если угол между образующими конусов равен 90°, то луч после двукратного отражения от поверхности конусов направляется в сторону РЛС, что и обеспечивает большое значение ЭПР. Достоинством биконического отражателя является равномерная диаграмма рассеяния в плоскости, перпендикулярной его оси.

Содержание

I.3.2.1.4. ЭПР шара.Для определения ЭПР большого (по сравнению с _и) шара с идеально проводящей гладкой поверхностью можно воспользоваться формулой (I.3.4). Однако в данном случае в этом нет необходимости, поскольку такой шар соответствует требованиям к гипоте­тической цели, площадь поперечного сечения которой и является ее ЭПР.

Таким образом, ЭПР шара (рис. I.3.9), имеющего и гладкую идеально проводящую поверхность, равна его площади поперечного сечения независимо от длины волны и направления облучения:

. (I.3.8)

Для малого шара с ЭПР определяется дифракци­онной формулой Рэлея и характеризуется сильной зависимостью от длины волны облучающих радиоволн.

Этот случай имеет место, например, при отражении радиоволн от капелек дождя и тумана. С учетом значения диэлектрической проницаемости воды ( = 80) ЭПР дожде­вых капель

, (I.3.9)

где d⁶_к – диаметр капель.

Полезно знать, что для любой гладкой выпуклой хорошо проводящей поверхности ЭПР

,

если радиусы кривизны в «блестящей точке» r₁ и r₂ много больше _и.

Под блестящей точкой понимают точку на отражающей поверхности, в которой нормаль совпадает с направлением на РЛС, т. е. происходит зеркальное отражение в ее сторону.

Содержание

I.3.2.1.5. ЭПР полуволнового линейного вибратора. Если линей­ный вибратор длиной l облучается вертикально поляризо­ванной волной с напряженностью электрического поля Е₁ по направлению, составляющему угол  с нормалью к вибратору (рис. I.3.10), то в нем возникает ток

,

где h_д — действующая высота вибратора; Z_ВХ— входное сопротивление вибратора.

При протекании тока возникает вторичное излучение, напряженность вертикально поляри­зованной компоненты которого в месте расположения РЛС

. (I.3.10)

Рис.I.3.10

Отсюда ЭПР вибратора:

. (I.3.11)

Для полуволнового вибратора, имеющего действую­щую высоту и выходное сопротивлениеОм, ЭПР. Значение s_в меняется от максимального при расположении виб­ратора параллельно вектору до s_в = 0 при его рас­положении перпендикулярно .

Так как поляризация излучаемого вибратором сигнала параллельна его оси, то при произвольной ориентации множество вибраторов создает неполяризованный сигнал, который принимается РЛС независимо от се собственной поляризации. Это позволяет использовать множество таких вибраторов в виде станиолевых лент для радиолокационной маскировки ЛА.