10

РОСТОВСКИЙ ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ СЕРВИСА И ТУРИЗМА

Южно-Российский государственный университет экономики и сервиса

____________________________________________________________________

Кафедра Радиоэлектроники

Лазаренко С.В.

ЛЕКЦИЯ № 17

ФИЛЬТР КАЛМАНА

по дисциплине “Радиотехнические цепи и сигналы”

Ростов-на-Дону

2010

ЛЕКЦИЯ 17

ФИЛЬТР КАЛМАНА

Время: 2 часа.

Изучаемые вопросы: 1 Формулировка задачи фильтрации

2 Уравнение фильтра Калмана

3 Пример построения фильтра Калмана

В данной лекции реализуются следующие элементы квалификационной характеристики:

1 Студент должен знать временные и спектральные характеристики детерминированных сигналов.

2 Студент должен уметь использовать методы спектрального и корреляционного анализа детерминированных и случайных сигналов.

3 Студент должен владеть приемами измерения основных параметров и характеристик радиотехнических цепей и сигналов.

1 ФОРМУЛИРОВКА ЗАДАЧИ ФИЛЬТРАЦИИ

При решении уравнения Винера-Хопфа возникают большие трудности, особенно при рассмотрении неустановившегося режима. Кроме того, создать идеальный фильтр Винера невозможно, так как переход от полосы пропускания к полосе задержания в нем происходит скачком. А это противоречит закону сохранения энергии. В реальных фильтрах такой переход является плавным. С другой стороны, задача реализации фильтра с найденной из уравнения Винера-Хопфа импульсной характеристикой решается более удобно с помощью вычислительных машин, если фильтр задан в виде алгоритма. Это требует перехода от импульсной характеристики к соответствующим дифференциальным уравнениям, что связано с громоздкими вычислениями.

Указанные трудности в значительной степени ограничили применение винеровских фильтров на практике и одновременно стимулировали поиски новых подходов к решению задачи оптимальной фильтрации случайных процессов.

Ниже будут рассмотрены основные понятия теории фильтров Калмана, которые оказались более приспособленными для решения практических задач фильтрации случайных процессов.

При синтезе фильтра Калмана предполагают, что полезный сигнал генерируется из белого шума с помощью так называемого формирующего фильтра в соответствии с алгоритмом

, (1)

где - белый шум, спектральная плотность которого равна (шум формирования);

и - заданные коэффициенты.

В общем случае уравнение (1) векторное, тогда величины , и являются матрицами.

Таким образом, предполагается, что закон формирования полезного сигнала из белого шума известен.

Уравнение (1) называют уравнением формирующего фильтра.

Например, дифференциальное уравнение, описывающее формирующий фильтр, имеет вид

. (2)

Введем обозначения

, .

Тогда вместо уравнения (2) можно записать систему

,

.

Перепишем эту систему в векторной форме

.

Обозначим

, , ,

, .

При этом уравнение (2) преобразовалось в выражение (1) в векторной форме

. (3)

В канале передатчика сигнал может быть каким-то образом преобразован (например, с использованием модуляции, кодирования и т. п.). В процессе распространения сигнала от передатчика к приемнику он подвергается воздействию шума, поэтому принимаемый сигнал описывается соотношением

, (4)

где - белый шум, спектральная плотность которого равна (шум измерения);

- заданный коэффициент.

Также как и для формирующего фильтра величины и могут быть вектором и матрицей соответственно. Уравнение (4) называют уравнением наблюдения.

На основании выражений (1) и (4) можно изобразить структурную схему процесса формирования принимаемого сигнала в векторной (рисунок 1).

Рисунок 1

2 УРАВНЕНИЕ ФИЛЬТРА КАЛМАНА

Получить уравнение фильтра Калмана можно из уравнения Винера-Хопфа в векторной форме. Опуская громоздкие выкладки, запишем это уравнение.

. (5)

Здесь - оптимальная оценка полезного сигнала, - коэффициент передачи (усиления) фильтра.

Так же как и в схеме формирования принимаемого сигнала все величины, в том числе , могут быть векторными (матричными).

Структурная схема алгоритма фильтра Калмана приведена на рисунке 2.

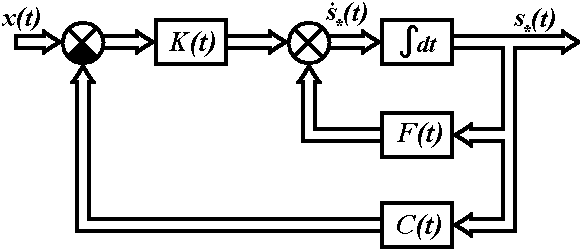
Рисунок 2

Следует обратить внимание на то, что практически все элементы фильтра Калмана такие же, как и в формирующем фильтре. Основная трудность состоит в определении коэффициента усиления фильтра. Он определяется из системы уравнений

. (6)

В этих уравнениях - матрица ошибок:

.

Второе уравнение системы (6) называется дисперсионным. Оно является нелинейным и не содержит принятого сигнала. Поэтому его можно решить до приема сигнала и использовать полученное решение для определения коэффициента усиления оптимального фильтра. В общем случае это уравнение не имеет аналитического решения. Поэтому необходимо использовать численные методы.

3 ПРИМЕР ПОСТРОЕНИЯ ФИЛЬТРА КАЛМАНА

Пусть формирующий фильтр представляет собой простейший фильтр нижних частот (рисунок 3).

Рисунок 3

На вход этого фильтра поступает напряжение в виде белого шума, спектральная плотность мощности которого постоянна и равна . С учетом этого, считая выходным сигналом напряжение на конденсаторе, имеем

, (7)

где - постоянная времени цепи.

Сравнивая выражения (7) и (1), делаем вывод, что

, .

Полагая в выражении (4) , запишем уравнение наблюдения

, (8)

где - белый шум, спектральная плотность мощности которого также постоянна и равна .

Уравнение фильтрации при этом будет выглядеть следующим образом:

,

где

.

Дисперсионное уравнение приведется к виду

.

Это нелинейное дифференциальное уравнение, которое может быть решено с использованием современных вычислительных средств.

На рисунках 4,5,6 приведены примеры (для различных начальных условий) работы одномерного фильтра Калмана, рассмотренного выше.

Рисунок 4

Рисунок 5

Рисунок 6

Лекцию подготовил старший преподаватель кафедры С. Лазаренко