Радиотехнические цепи и сигналы. Лазаренко С.В / Презентации РТЦиС / семестр зимний / часть2 / лек23

12

РОСТОВСКИЙ ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ СЕРВИСА И ТУРИЗМА

Южно-Российский государственный университет экономики и сервиса

__________________________________________________________________

Кафедра Радиоэлектроника

Лазаренко С.В.

ЛЕКЦИЯ № 23

ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ И Z-ПРЕОБРАЗОВАНИЕ

по дисциплине “Радиотехнические цепи и сигналы”

г. Ростов-на-Дону

2010 г.

ЛЕКЦИЯ 23

ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ И Z-ПРЕОБРАЗОВАНИЕ

Изучаемые вопросы: 1 Спектральная плотность дискретного сигнала

2 Дискретное преобразование Фурье и его основные свойства

3 Быстрое преобразование Фурье

4 Z-преобразование

1 СПЕКТРАЛЬНАЯ ПЛОТНОСТЬ ДИСКРЕТНОГО СИГНАЛА

Основное свойство дискретного сигнала заключается в том, что его значения определены не во все моменты времени, а лишь в счетном множестве точек. Если аналоговый сигнал имеет математическую модель вида непрерывной или кусочно-непрерывной функции, то отвечающий ему дискретный сигнал представляет собой последовательность отсчетных значений сигнала в точках соответственно.

На практике, как правило, отсчеты дискретных сигналов берут во времени через равный промежуток , называемый интервалом (шагом) дискретизации:

. (1)

Операцию дискретизации, т.е. перехода от аналогового сигнала к дискретному сигналу , можно описать, введя в рассмотрение т.н. дискретизирующую последовательность

, (2)

где - дельта – функция.

Структурная схема устройства для дискретизации аналогового сигнала приведена на рисунке 1.

Рисунок 1

Импульсный модулятор представляет собой устройство с двумя входами, на один из которых подается аналоговый сигнал . На второй вход поступают короткие синхронизирующие импульсы с интервалом повторения . Обозначим частоту повторения импульсов через .

Модулятор построен таким образом, что в момент подачи каждого синхроимпульса происходит измерение мгновенного значения сигнала . На выходе модулятора возникает последовательность импульсов, каждый из которых имеет площадь, пропорциональную соответствующему отсчетному значению аналогового сигнала. Сигнал в этом случае называется модулированной импульсной последовательностью. Если длительность импульсов постоянна, то соответствует амплитудно-импульсной модуляции.

Описанный принцип позволяет записать следующую математическую модель дискретного сигнала, полученного путем импульсной модуляции

. (3)

Фактически это есть произведение двух сигналов и . Найдем спектральную плотность этого дискретного сигнала в предположении, что известна спектральная плотность сигнала .

Для этого вначале вспомним, что спектральная плотность произведения двух сигналов есть свертка спектральных плотностей этих сигналов

, (4)

где - спектральная плотность сигнала (2).

Для нахождения представим рядом Фурье, учитывая, что - период следования - импульсов:

, (5)

где коэффициенты ряда определяются обычным образом

. (6)

При выводе выражения (6) учтено фильтрующее свойство - функции. С учетом полученного результата формула (5) приобретает вид:

. (7)

Учитывая, что преобразованию Фурье присуще свойство линейности, спектральную плотность сигнала (7) можно определить, суммируя спектральные плотности функций вида .

(8)

Проверить правильность выражения (8) можно, определив обратное преобразование Фурье.

Таким образом, имеем

. (9)

Подставив (9) в (4), получим окончательно

(10)

Таким образом, спектр дискретизированного сигнала представляет собой результат суммирования бесконечного числа "копий" спектра исходного сигнала. Эти копии располагаются на оси частот через промежутки , равные частоте дискретизации .

2 ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ И ЕГО ОСНОВНЫЕ СВОЙСТВА

При исследовании сигналов с помощью цифровых ЭВМ непрерывный сигнал на интервале времени наблюдения задается своими отсчетными значениями , , ... , , взятыми соответственно в моменты времени , , , ..., . Полное число отсчетов . Массив этих чисел является единственной информацией, по которой можно судить о спектральных свойствах сигнала .

Методика изучения таких дискретных сигналов состоит в том, что полученная выборка отсчетных значений как бы повторяется бесконечное число раз. В результате сигнал становится периодическим с периодом Т (рисунок 2).

Рисунок 2

Такому сигналу можно сопоставить некоторую математическую модель, раскладывая которую в ряд Фурье, можно найти соответствующие амплитудные коэффициенты. Совокупность этих коэффициентов образует спектр дискретного периодического сигнала.

Воспользуемся моделью сигнала в виде последовательности -импульсов

(11)

Эта модель отличается от (3) ограниченным количеством отсчетов (сигнал рассматривается в пределах "периода" Т). Представим сигнал (11) комплексным рядом Фурье

, (12)

где коэффициенты

. (13)

Подставим в выражение (13) значение (11), и учтем что .

.

Введем безразмерную переменную . Тогда , . При , при

При этом получим

(14)

Эта формула и определяет дискретное преобразование Фурье (ДПФ) дискретного сигнала .

Из (14) следуют основные свойства ДПФ.

2.1 Дискретное преобразование Фурье есть линейное преобразование, т.е. сумме сигналов отвечает сумма их ДПФ.

2.2 Количество различных коэффициентов, , , ... , вычисляемых по формуле (14), равно числу отсчетов за период: при коэффициент (показать).

2.3 Коэффициент (постоянная составляющая) является средним значением всех отсчетов

. (15)

2.4 Если N - четное, то

. (16)

2.5 Если - четное и - вещественные числа, то коэффициенты ДПФ, номера которых располагаются симметрично относительно , образуют комплексно-сопряженные пары. Действительно,

. (17)

Второй сомножитель в правой части выражения (17) всегда равен 1, Следовательно,

. (18)

Если на основании совокупности отсчетов , , ... , , некоторого сигнала найдены коэффициенты ДПФ , , , ... , то по ним всегда можно восстановить исходный сигнал с ограниченным спектром, который был подвергнут дискретизации. Ряд Фурье такого сигнала принимает вид конечной суммы:

где - фазовый угол коэффициента ДПФ.

Формула (13) позволяет ввести в рассмотрение обратное ДПФ. Если положить t и учесть, что суммируется конечное число членов ряда, то получим

.

3 БЫСТРОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ

Как видно из формул, полученных на предыдущей лекции, для нахождения ДПФ или ОДПФ последовательности из N элементов, требуется выполнить операций с комплексными числами. Если длины обрабатываемых массивов имеют порядок тысячи или более, то использовать эти алгоритмы дискретного спектрального анализа в реальном масштабе времени затруднительно из-за ограниченного быстродействия вычислительных устройств.

Выходом из положения явился алгоритм быстрого преобразования Фурье (БПФ), предложенный в 60-х годах. Существенно сократить число выполняемых операций здесь удается за счет того, что обработка входного массива сводится к нахождению ДПФ (или ОДПФ) массивов с меньшим числом членов.

Будем предполагать, и это существенно для метода БПФ, что число отсчетов где — целое число.

Разобьем входную последовательность на две части с четными и нечетными номерами:

, , (1)

и представим -ный коэффициент ДПФ в виде

.

Непосредственно видно, что первая половина коэффициентов ДПФ исходного сигнала с номерами от до выражается через коэффициенты ДПФ двух частных последовательностей:

, (2)

.

Теперь учтем, что последовательности коэффициентов, относящихся к четной и нечетной частям входного массива, являются периодическими с периодом :

, .

Кроме того, входящий в формулу (2) множитель при можно преобразовать так:

.

Отсюда находим выражение для второй половины множества коэффициентов ДПФ:

, (3)

.

Формулы (2) и (3) лежат в основе алгоритма БПФ. Далее вычисления строят по итерационному принципу: последовательности отсчетов с четными и нечетными номерами вновь разбивают на две части. Процесс продолжают до тех пор, пока не получится последовательность, состоящая из единственного элемента. Легко видеть, что ДПФ этого элемента совпадает с ним самим.

Можно показать, что число операций, необходимых для вычисления БПФ, оценивается как .

4 Z-ПРЕОБРАЗОВАНИЕ

При анализе и синтезе дискретных и цифровых устройств широко используют так называемое Z-преобразование, играющее по отношению к дискретным сигналам такую же роль, как интегральные преобразования Фурье и Лапласа по отношению к непрерывным сигналам. В данной лекции излагаются основы теории этого функционального преобразования и некоторые его свойства.

Определение Z-преобразования. Пусть - числовая последовательность, конечная или бесконечная, содержащая отсчетные значения некоторого сигнала. Поставим ей в однозначное соответствие сумму ряда по отрицательным степеням комплексной переменной :

. (1)

Назовем эту сумму, если она существует, Z-преобразованием последовательности . Целесообразность введения такого математического объекта связана с тем, что свойства дискретных последовательностей чисел можно изучать, исследуя их Z -преобразования обычными методами математического анализа.

На основании формулы (1) можно непосредственно найти Z – преобразования дискретных сигналов с конечным числом отсчетов. Так, простейшему дискретному сигналу с единственным отсчетом соответствует . Если же, например, , то

.

Сходимость ряда. Если в ряде (1) число слагаемых бесконечно велико, то необходимо исследовать его сходимость. Из теории функций комплексного переменного известно следующее. Пусть коэффициенты рассматриваемого ряда удовлетворяют условию

(2)

при любых . Здесь и — постоянные вещественные числа. Тогда ряд (1) сходится при всех значениях , таких, что . В этой области сходимости сумма ряда представляет собой аналитическую функцию переменной , не имеющую ни полюсов, ни существенно особых точек.

Рассмотрим, например, дискретный сигнал , образованный одинаковыми единичными отсчетами и служащий моделью обычной функции включения. Бесконечный ряд

является суммой геометрической прогрессии и сходится при любых в кольце . Суммируя прогрессию, получаем

На границе области аналитичности при эта функция имеет единственный простой полюс.

Аналогично получается Z-преобразование бесконечного дискретного сигнала , где — некоторое вещественное число. Здесь

.

Данное выражение имеет смысл в кольцевой области |.

Z-преобразование непрерывных функций. Полагая, что отсчеты есть значения непрерывной функции в точках , любому сигналу можно сопоставить его Z-преобразование при выбранном шаге дискретизации :

Например, если , то соответствующее Z-преобразование

является аналитической функцией при .

Пусть — функция комплексной переменной , аналитическая в кольцевой области . Замечательное свойство Z-лреобразования состоит в том, что функция определяет всю бесконечную совокупность отсчетов .

Действительно, умножим обе части ряда (1) на множитель:

,

а затем вычислим интегралы от обеих частей полученного равенства, взяв в качестве контура интегрирования произвольную замкнутую кривую, лежащую целиком в области аналитичности и охватывающую все полюсы функции . При этом воспользуемся фундаментальным положением, вытекающим из теоремы Коши:

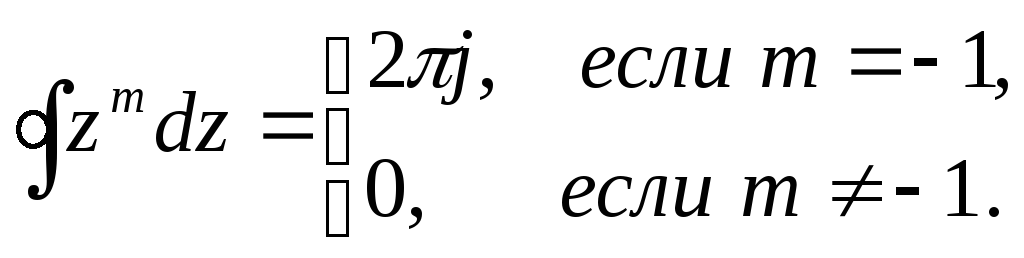(3)

Для доказательства этого найдем следующие интегралы:

.

Каждый из них находится заменой произвольного контура интегрирования на окружность постоянного радиуса , равного модулю переменной , т.е. фактически производится замена

.

При этом, так как радиус есть величина постоянная, то интегрирование производится по углу в пределах от 0 до . Первый интеграл равен

. (4)

Второй интеграл вычисляется аналогично

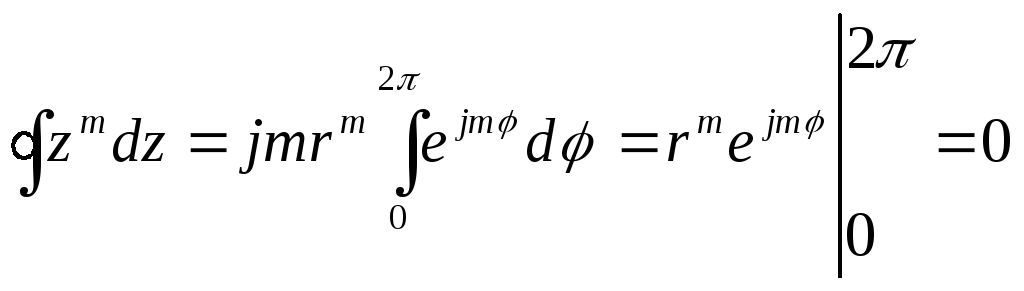. (5)

Третий интеграл вычислится следующим образом:

. (6)

Не трудно убедиться, что четвертый интеграл так же, как первые два, равен нулю.

Очевидно, интегралы от всех слагаемых правой части обратятся в нуль, за исключением слагаемого с номером , поэтому

. (8)

Данная формула называется обратным z-преобразованием.

Найдем связь Z –преобразования с преобразованиями Лапласа и Фурье. Для этого представим числовую последовательность в виде, рассмотренном в лекции 30 (формула 11)

.

Преобразуя это выражение по Лапласу, получим

.

Если выполнить подстановку , то это выражение переходит в Z – преобразование. Если же положить , то выражение

будет преобразованием Фурье импульсной последовательности.

Этот факт дает возможность проводить аналогию между спектральными свойствами непрерывных и дискретных сигналов.

Основные свойства z-преобразования.

1. Линейность. Если и — некоторые дискретные сигналы, причем известны соответствующие Z-преобразования и , то сигналу будет отвечать преобразование при любых постоянных и . Доказательство проводится путем подстановки суммы в формулу (1).