5 Стационарный режим автогенератора

Ранее была рассмотрена так называемая линейная теория автогенератора, в основе которой лежит замена исходного нелинейного дифференциального уравнения генератора соответствующим линейным уравнением. Эта теория позволила нам установить условия самовозбуждения генератора.

Однако линейная теория не позволяет определить параметры стационарного режима генератора, например, амплитуду колебаний, так как, при колебания должны нарастать до бесконечности.

Стационарные амплитуды напряжений и токов, очевидно, можно найти лишь при условии учета нелинейности характеристики транзистора, ибо эта нелинейность и является, в конечном счете, причиной установления автоколебаний в генераторе. В самом деле, при увеличении "размаха" колебаний усилительные способности транзистора ухудшаются (напряжение на входе транзистора заходит в области с малыми значениями крутизны), и нарастание колебаний в конце концов прекращается.

В установившемся состоянии автогенератор создает электрические колебания, форма которых из-за влияния нелинейности в какой-то степени отличается от косинусоидальной. Если, однако, нагрузкой генератора является колебательный контур с высокой добротностью, приближенно можно полагать, что напряжение на контуре, а, следовательно, на входе транзистора, изменяется во времени по гармоническому закону. Влиянием высших гармонических составляющих выходного тока транзистора в этом случае можно пренебречь.

Такое допущение означает, что вместо обычной крутизны , которая является функцией мгновенного напряжения на входе транзистора, можно воспользоваться средней крутизной, т.е. параметром по первой гармонике:

,

где - амплитуда первой гармоники выходного тока транзистора;

- амплитуда входного напряжения.

Средняя крутизна в пределах одного периода колебаний считается постоянной (система как бы линейна). Вместе с тем является функцией амплитуды колебаний, т.е. изменение амплитуда нарушает линейность системы.

Такая линеаризация системы позволила разработать сравнительно простые методы расчета стационарных параметров автоколебаний генератора, среди которых наибольшее распространение получил квазилинейный метод.

6 Квазилинейный метод

Квазилинейный метод разработан советским ученым Ю.Б.Кобзаревым. Он основан на использовании соотношений между первыми гармониками токов и напряжений и замене нелинейного элемента цепи эквивалентным линейным, характеризуемым средним по первой гармонике параметром . После такой замены нелинейная цепь описывается линейными уравнениями и может исследоваться методами линейной теории (например, символическим методом). Нелинейность цепи проявляется в зависимости средней крутизны от амплитуды входного напряжения. При этом высшие гармоники во внимание не принимаются, так как они отфильтровываются узкополосной избирательной цепью.

Понятие средней крутизны лежит в основе квазилинейного метода. Поэтому рассмотрим эту характеристику несколько подробнее.

На рисунке 1,а изображена вольтамперная характеристика нелинейного элемента. Начало координат на графике совмещено с положением исходной рабочей точки. Справа показана форма тока при двух значениях амплитуды входного напряжения. При малых амплитудах ток совпадает по форме с приложенным напряжением (система ведет себя, как линейная), при больших колебания выходят за пределы линейного участка вольтамперной характеристики, и форма тока оказывается негармонической.

На рисунке 1,б также показаны токи первых гармоник, соответствующие малой и большой амплитудам входного напряжения. Слева обычным графическим способом получены характеристики, которыми обладал бы нелинейный элемент, если бы ток не содержал высших гармонических составляющих. Этот график, с одной стороны, показывает, что пренебрежение высшими гармониками эквивалентно линеаризации вольтамперной характеристики НЭ. С другой стороны, из графика следует, что нелинейные свойства элемента по отношению к амплитуде входного напряжения сохраняются - при изменении меняется наклон линеаризованной характеристики, т.е. крутизна по первой гармонике .

Функцию , лежащую в основе расчетов цепей квазилинейным методом, рассчитывают аналитически либо получают экспериментально. При этом вид ее определяется как формой ВАХ НЭ, так и положением исходной рабочей точки на ней.

Получим, например, уравнение при степенной аппроксимации ВАХ НЭ.

Если ВАХ НЭ имеет вид

,

то, подставив в это уравнение значение , получим

.

Заменив степени косинусов тригонометрическими функциями кратных аргументов и выделив первую гармонику тока, имеем:

.

Отсюда

.

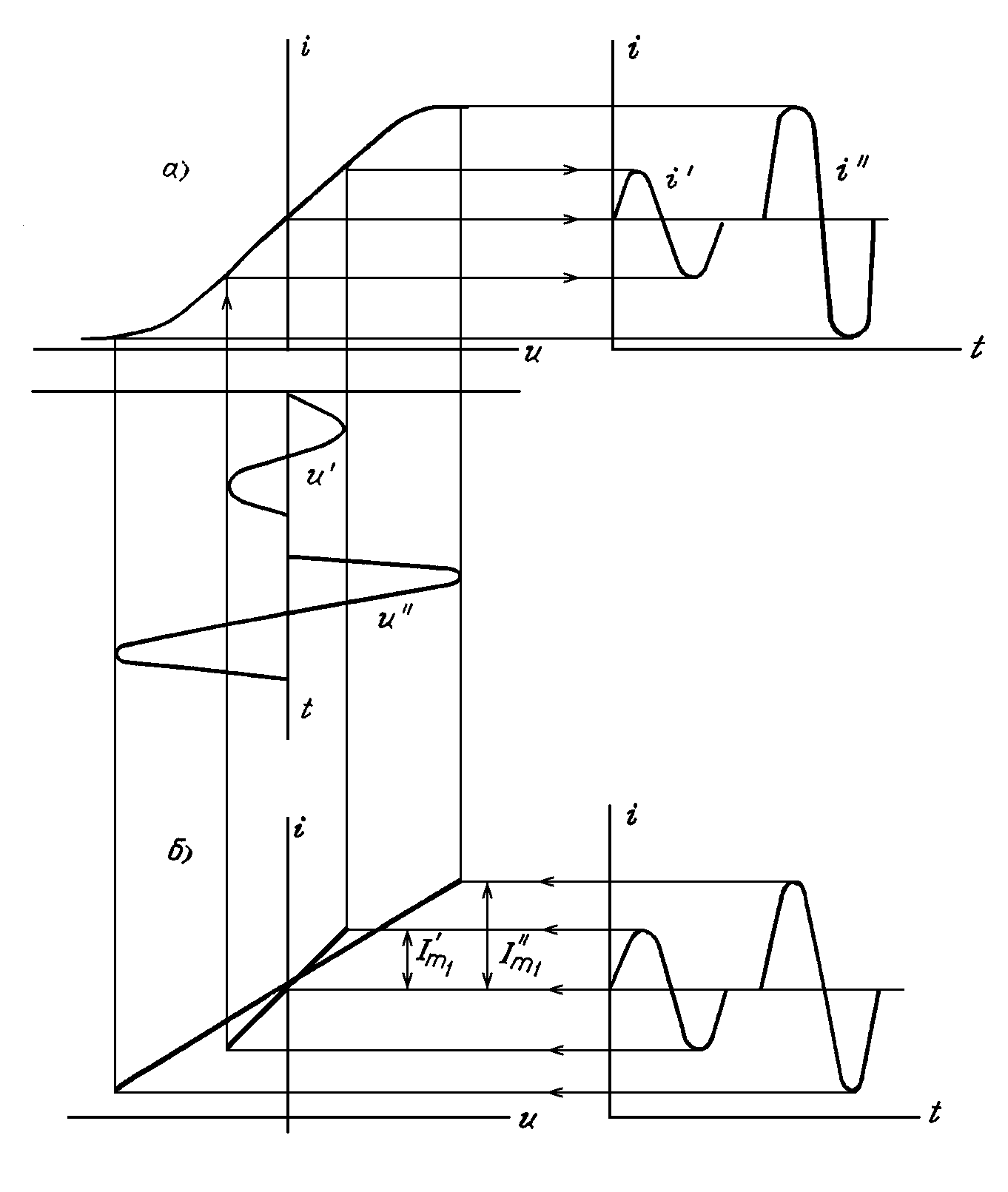
Рисунок 1

Соотношение (2) позволяет найти значение при любой амплитуде входного напряжения . Функцию можно получить и экспериментально. Для этого нужно снять зависимость значений амплитуда первой гармоники выходного напряжения от амплитуды входного напряжения и выполнить расчет по формуле (1).

Типичные зависимости при характерных значениях напряжения смещения приведены на рисунке 2.

Рисунок 2

Используем квазилинейный метод для определения амплитуды и частоты стационарных колебаний генератора. В соответствии с изложенным выше будем полагать, что переменные токи и напряжения в цепях автогенератора изменяются во времени по гармоническому закону. Тогда вместо системы интегро-дифференциальных уравнений для установившегося состояния можно написать систему алгебраических уравнений, в которую входят соответствующие комплексные амплитуды:

. (3)

Здесь - угловая частота автоколебаний. Подставляя во второе уравнение значения и из первого и третьего уравнений, получаем:

. (4)

Так как (переменные составляющие входного напряжения и тока в транзисторе изменяются в фазе), из выражения (4) будем иметь:

.

Отсюда следует, что

; (5)

. (6)

Эти выражения и определяют параметры автоколебаний в стационарном режиме.

Из равенства (5) видно, что угловая частота автоколебаний в установившемся режиме

,

т.е. совпадает с резонансной частотой контура.

Стационарная амплитуда напряжения на входе транзистора согласно равенству (6) представляет собой величину, при которой

. (7)

Чтобы определить необходимо построить график и по нему найти величину , соответствующую значению (рисунок 3).

а) б)

Рисунок 3

Соотношения, свойственные квазилинейному методу, могут быть получены и из нелинейного дифференциального уравнения генератора

. (8)

Заменяя в (8) напряжение и ток их первыми гармониками и полагая, что , получим уравнение

, (9)

являющееся линейным для постоянной амплитуда напряжения . В стационарном режиме генератор эквивалентен контуру с коэффициентом затухания

.

Колебания в контуре происходят с частотой и будут незатухающими, если в , т.е. при . Результаты данного анализа хорошо согласуются с полученными ранее.

Наличие на графике (рисунок 3,б) двух значений стационарных амплитуд (что физически быть не может) ставит вопрос об устойчивости стационарных режимов генератора. Говорят, что стационарный режим автоколебательного процесса устойчив, если при любых малых отклонениях амплитуды гармонических колебаний от стационарного уровня система вновь стремится вернуться к состоянию со стационарной амплитудой.

Рассмотрим устойчивость режима с амплитудой (точка 1). Допустим, что по каким-либо причинам амплитуда получила приращение . Так как на этом участке графика при увеличении амплитуды входного напряжения увеличивается и (растет усиление), то амплитуда увеличивается еще больше, т.е. значение является неустойчивым (рассуждения при отклонении аналогичны). В точке 2 случайное увеличение амплитуды на приводит к уменьшению усиления, что способствует возвращению амплитуды к стационарному состоянию. Следовательно, значение является устойчивым. По тем же причинам единственный стационарный режим генератора на графике 3,а также является устойчивым.

Анализируя сказанное, можно окончательно записать условие устойчивости стационарного режима генератора в виде:

. (10)