16

РОСТОВСКИЙ ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ СЕРВИСА И ТУРИЗМА

Южно-Российский государственный университет экономики и сервиса

_________________________________________________________________

Кафедра Радиоэлектроника

Лазаренко С.В.

ЛЕКЦИЯ № 21

Активные цепи с обратными связями

по дисциплине “Радиотехнические цепи и сигналы”

Ростов-на-Дону

2011

ЛЕКЦИЯ № 21

Активные цепи с обратными связями

по дисциплине "РАДИОТЕХНИЧЕСКИЕ ЦЕПИ СИГНАЛЫ"

Изучаемые вопросы:

1 Виды обратной связи.

2 Основные характеристики и свойства цепей с обратной связью.

Цепи с обратной связью

Обратной связью (ОС) в общем случае называется явление передачи отклика системы, возникающего в результате какого-либо внешнего воздействия, обратно на ее вход. Понятие "обратная связь" широко используется в самых различных видах систем: технических, кибернетических, экономических, биологических и т.п. Рассмотрим обратную связь в более узком смысле, применительно к радиотехническим цепям, в которых она используется для улучшения различных характеристик этих цепей, а также для осуществления автоколебательных режимов работы.

1. Виды обратной связи

В радиотехнических цепях различает положительную (ПОС) и отрицательную (ООС) обратные связи. Положительная обратная связь поддерживает внешнее воздействие, отрицательная - противодействует ему. При любом знаке ОС в цепи, охваченной этой связью, обнаруживается замкнутая цепь зависимостей.

Принцип ОС применительно к усилительным устройствам поясняется структурной схемой, изображенной на рисунке 1.

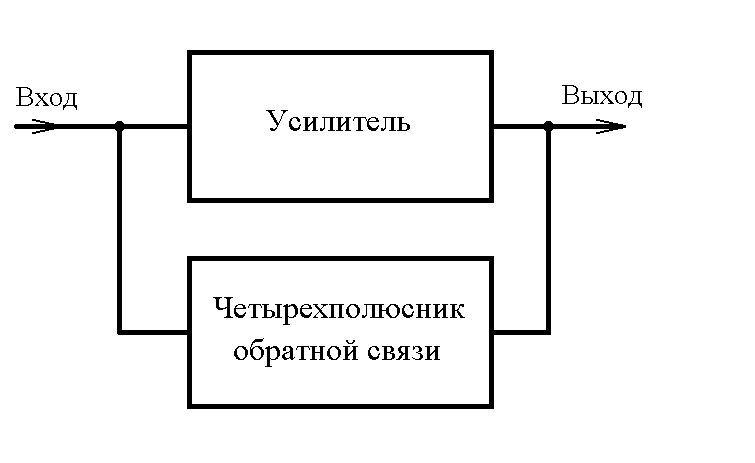
Рисунок 1

Схема включает в себя два основных элемента: усилитель и четырехполюсник обратной связи. При этом ЧОС может быть как пассивным, так и активным.

Получим выражение для коэффициента передачи цепи с обратной связью. Для этого рассмотрим функциональную схему, изображенную на рисунке 2.

На схеме обозначено:

- напряжение на входе всей цепи с ОС;

Рисунок 2

- напряжение на выходе цепи с ОС;

- напряжение на выходе четырехполюсника обратной связи (ЧОС);

- коэффициент усиления усилителя при разомкнутой цепи ОС;

- коэффициент передачи ЧОС;

- напряжение на входе усилителя.

Особенностью схемы является то, что часть выходного сигнала, зависящая от величины , подается обратно на вход и вместе с входным сигналом образует входное напряжение усилителя . Эта обратная подача напряжения придает цепи с ОС свойства, существенно отличающие ее от цепи без ОС.

Основной интерес представляет передаточная функция (коэффициент передачи) всей цепи в целом . Для определения этой функции воспользуемся следующими очевидными соотношениями:

;

.

Тогда

.

Решая последнее уравнение относительно , получим

,

откуда

. (1)

Функцию иногда называют комплексным коэффициентом передачи замкнутой цепи, а произведение - комплексным коэффициентом передачи разомкнутой цепи.

Сопоставление с позволяет определить знак обратной связи. Если на заданной частоте

,

то введение ОС уменьшает модуль коэффициента передачи цепи и, следовательно, амплитуду выходного сигнала - в цепи наблюдается ООС.

Если имеет место обратное неравенство

,

то в цепи наблюдается ПОС.

При усиление становится бесконечно большим. Это означает, что цепь становится неустойчивой, в ней возможно возникновение автоколебаний.

Схемное выполнение обратной связи может быть весьма разнообразным. По способу введения напряжения ОС в цепь входа различают последовательную и параллельную ОС. При последовательной ОС источник входного сигнала, выход ЧОС и вход усилителя соединяются последовательно, а при параллельной ОС - параллельно.

По способу снятия напряжения на ЧОС различают ОС по напряжению и ОС по току. Схема с ОС по напряжению характеризуется тем, что выход усилителя, вход ЧОС и нагрузка соединены параллельно, т.е. напряжение ОС пропорционально выходному напряжению. При ОС по току эти элементы цепи соединены последовательно, т.е. напряжение ОС пропорционально току. На рисунке 3 изображены схемы с последовательной ОС по напряжению (рисунок 3,а) и по току (рисунок.3,6), а также схемы с параллельной ОС по напряжению (рисунок 2,в) и по току (рисунок 3,г).

а) б)

в) г)

Рисунок 3

2. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ И СВОЙСТВА ЦЕПЕЙ С ОБРАТНОЙ СВЯЗЬЮё

Обратная связь широко применяется в различных радиотехнических устройствах: усилителях, генераторах автоколебаний, запо­минающих устройствах ЭВМ и т.п. В усилителях, например, значительно чаще используется ООС, улучшающая многие качественные показатели усилителя, в схемах генераторов преобладает ПОС, которая является принципиально необходимой для возникновения автоколебаний.

Рассмотрим действие ООС в усилителях. Оно проявляется в том, что:

- повышается стабильность коэффициента усиления при изменении питающих напряжений, величины нагрузки, смене ламп и транзисторов;

- уменьшаются линейные (частотные и фазовые) искажения, вносимые усилителем, повышается его широкополосность;

- снижается уровень нелинейных искажений и собственных помех усилителя, что приводит к увеличению его динамического диапазона;

- возрастает входное и уменьшается выходное сопротивление усилителя, что способствует лучшему согласованию усилителей при их каскадном соединении;

- уменьшаются переходные искажения, в частности, уменьшается время установления напряжения, спада и т.д.;

- уменьшаются фазовые сдвиги между входными и выходными сигналами, влияющие как на запаздывание сигнала во времени, так и на его форму.

Введение OOС влечет за собой и нежелательные результаты, которые, как правило, не являются существенными. Например, в большинстве случаев уменьшается общий коэффициент усиления устройства, повышается вероятность возникновения паразитной генерации, обусловленная тем, что ОС, заданная в рабочем диапазоне частот как отрицательная, на некоторых частотах из-за присущих усилителю фазовых сдвигов становится положительной. Все это требует принятия специальных мер, несколько усложняет схемы усилителей.

Рассмотрим некоторые количественные соотношения в усилителях с ООС, подтверждающие вышесказанное.

Например, вопрос о стабилизации коэффициента усиления легко решить, продифференцировав по основное соотношение для цепей с ОС (1). При этом для упрощения расчетов будем полагать все величины вещественными

,

откуда находим относительное изменение коэффициента усиления цепи с обратной связью

.

Для отрицательной ОС и

.

Отсюда следует, что относительная нестабильность коэффициента усиления при ООС уменьшается в раз. При очень глубокой ООС вообще очень мало зависит от , т.к. при

.

Существенно заметить, что обратной связью уменьшается нестабильность, возникающая в цепи усилителя. Нестабильность в ЧОС не ослабляется. Действительно,

,

откуда

.

При очень глубокой ООС

.

Вышеизложенное свидетельствует, что при применении ООС особое внимание должно быть обращено на повышение стабильности ЧОС. На практике осуществление этого требования облегчается, тем, что основные дестабилизирующие факторы возникают в самом усилителе, содержащем активные элементы (радиолампы, транзисторы) и элементы нагрузки. ЧОС обычно является пассивной цепью и может быть выполнен достаточно стабильным.

Уменьшение линейных искажений в усилителе с ООС связано с выравниванием его АЧХ и ФЧХ за счет ООС. Действительно, при

и при (частотно-независимая ОС) отрешится к постоянной величине. Иначе говоря, АЧХ усилителя с ООС почти не зависит от частотных свойств собственно усилителя и определяется главным образом частотными свойствами ЧОС.

Физически эффект сглаживания АЧХ за счет ООС можно пояснить так. Величина напряжения ОС, подаваемого с выхода усилителя на его вход, в соответствии с АЧХ собственно усилителя различна на разных частотах. В области частот, где имеется подъем АЧХ, ОС сильнее ослабляет усиление по сравнению с частотами, где имеется западание АЧХ. Таким образом, неравномерность АЧХ сглаживается, а полоса пропускания усилителя расширяется.

Нелинейные искажения, возникающие в усилителе из-за нелинейности ВАХ его активных элементов и проявляющиеся в появлении на выходе высших гармоник усиливаемого сигнала, также уменьшаются ООС в раз. Это объясняется тем, что введение ООС приводит к уменьшению усиления в раз в одинаковой мере для полезного сигнала и для гармоник. Однако это уменьшение для полезного сигнала компенсируют тем, что увеличивают входное напряжение в раз, т.е. доводят уровень сигнала на выходе до той же величины, которая была бы в усилителе без ОС. Этим обеспечивается корректность сравнения нелинейных искажений, ибо нелинейные свойства усилителей зависят от уровня входного сигнала, что требует производить сравнение только при одинаковом эффекте на выходе устройства с ОС и без нее.

Таким образом, уровень полезного сигнала на выходе достигает той же величины, которая была бы без ОС, а гармоники и помехи, возникавшие в той части усилителя, которая охвачена ОС, ослабляются, т.е. коэффициент нелинейных искажений уменьшается.

Наличие ОС в усилителе существенно изменяет его входное сопротивление. Степень и характер этого изменения зависит от вида ОС (последовательная или параллельная) и ее глубины.

Рассмотрим влияние ООС на входное сопротивление усилителя с последовательной ОС по напряжению (рис. 5.2,а).

Для источника сигнала усилитель представляет собой нагрузку с сопротивлением

,

где - входное сопротивление собственно усилителя;

- входное сопротивление усилителя с ОС.

После несложных преобразований получаем:

.

При ООС и вещественных и

.

Полученный результат показывает, что входное сопротивление усилителя за счет ООС возрастает в раз, вследствие чего шунтирующее действие усилителя на предыдущий каскад уменьшается. Это улучшает условия согласования усилительных каскадов, особенно схем на транзисторах.

3 ОБЩИЕ СВЕДЕНИЯ ОБ УСТОЙЧИВОСТИ

В цепях с ОС при определенных условиях возможно самопроизвольное изменение стационарного режима работы, например, возникновение автоколебаний. Если в схемах генераторов получение автоколебаний является их основной функцией, то в схемах усилителей, модуляторов, детекторов, преобразователей возникновение автоколебаний в большинстве случаев не только нежелательно, но совершенно недопустимо. Поэтому применение ОС в радиотехнических цепях тесно связано с проблемой обеспечения устойчивой работы этих цепей.

Общий вопрос об устойчивости, т.е. о том, могут или не могут в данной цепи возбудиться автоколебания, решается на основании некоторых общих признаков, выражаемых при помощи так называемых критериев устойчивости. В настоящее время известно несколько критериев, отличающихся больше по форме, нежели по существу. Различают алгебраические и частотные критерии устойчивости.

Алгебраические критерии устойчивости определяют условия устойчивости в виде алгебраических неравенств, составленных из коэффициентов дифференциального уравнения цепи. Частотные критерии устойчивости выражаются в виде условий, предъявляемых к частотным характеристикам цели с ОС с целью обеспечения их устойчивой работы.

В основе большинства критериев лежит критерий устойчивости решения дифференциального уравнения, описывающего исследуемую цепь. В общем случае это уравнение является линейным неоднородным с постоянными коэффициентами, решение которого находится в виде суммы свободной и принужденной (установившейся) составляющей. Очевидно, для суждения об устойчивости цепи необходимо рассмотреть поведение свободной составляющей отклика цепи . Если выполняется условие

,

то цепь устойчива, если

,

то цепь неустойчива.

Свободная составляющая отклика находится как решение однородного дифференциального уравнения

, (1)

где - искомые напряжения или токи в цепи;

- действительные числа, зависящие от параметров цепи.

Решение этого уравнения, как известно, имеет вид:

, (2)

где - постоянные интегрирования, определяемые из начальных условий;

- корни характеристического уравнения.

. (3)

Для обеспечения устойчивости цепи необходимо, чтобы все слагаемые уравнения (2) с течением времени уменьшались (затухали), т.е. показатели экспонент должны иметь отрицательные знаки. Другими словами, цепь с обратной связью является устойчивой, если все действительные корни или действительные части всех комплексно-сопряженных корней характеристического уравнения цепи отрицательны. Это фундаментальное положение было обосновано известным русским ученым А.М. Ляпуновым, который в 90-х годах прошлого века заложил основы теории устойчивости.

Таким образом, исследование устойчивости радиотехнических цепей сводится к определению знаков действительных частей корней характеристического уравнения цепи.

4 КРИТЕРИЙ УСТОЙЧИВОСТИ РАУСА-ГУРВИЦА

В тех случаях, когда радиотехническая цепь описывается дифференциальным уравнением высокого порядка, определение корней характеристического уравнения, необходимое для суждения об устойчивости цепи, является довольно сложной задачей, решаемой, как правило, приближенно. Поэтому разработан ряд специальных приемов, позволявших определить условия отрицательности действительных частей корней без расчета самих корней. Анализируются лишь соотношения между коэффициентами дифференциального уравнения.

Наибольшее распространение среди этих приемов получил критерий Рауса-Гурвица.

Согласно этому критерию для устойчивости цепи необходимо и достаточно, чтобы определитель Гурвица и все его главные (диагональные) миноры были положительными.

Для составления определителя Гурвица из коэффициентов дифференциального (характеристического) уравнения цепи -й степени необходимо сначала выписать по главной диагонали определителя все коэффициенты от до в порядке возрастания индексов снизу вверх. Затем следует дополнить столбцы определителя под диагональными элементами коэффициентами с последовательно возрастающими индексами, а над ними - с последовательно убывающими. Все коэффициенты, индексы которых больше или отрицательны, заменяется нулями.

В общем виде определитель Гурвица записывается так:

.

Диагональные миноры образуется путем отбрасывания нижних строк и правых столбцов и имеет вид:

; ; ,

и т.д.

Если определитель Гурвица раскрыть по элементам правого столбца, то видно, что - требование положительности определителя Гурвица всегда сводится к требованию положительности свободного члена уравнения .

Итак, условия устойчивости цепей -го порядка представляет собой систему детерминантных неравенств:

Критерий Рауса-Гурвица определяет необходимее и достаточное условие устойчивости цепей. Однако имеет смысл выяснить только необходимые условия устойчивости, так как это позволит избежать излишних расчетов по методу Гурвица, если необходимые условия для цепи не выполняются.

Для определенности будем считать, что . Этого всегда можно добиться путем умножения всех членов характеристического уравнения на . Из алгебры известно, что уравнение (3) можно представить в виде:

. (4)

Отрицательные действительные корни , , …, дадут в уравнении (4) сомножители следующего вида:

. (5)

Если раскрыть в этом выражении скобки и произвести перемножение, то получим члены только с положительными коэффициентами, так как, перемножая и складывая положительные величины, мы не можем получить ни отрицательных чисел, ни нулей.

Пара комплексно-сопряженных корней , с отрицательными действительными частями дает в выражении (6.12) сомножители вида

. (6)

Очевидно, что произведение таких сомножителей независимо от их количества тоже даст члены только с положительными коэффициентами.

Уравнение (4) после раскрытия всех скобок и приведения подобных членов можно привести к уравнению(3). Учитывая, что , а также результаты перемножения сомножителей вида (5) и (6), можно утверждать, что все коэффициенты характеристического (дифференциального) уравнения устойчивой цепи положительны. Это условие является необходимым, но недостаточным , что означает, что если все коэффициенты положительны, то цепь может быть как устойчивой, так и неустойчивой. Для окончательного суждения необходимо провести расчеты по критерию Рауса-Гурвица. Но если среди коэффициентов имеется один или несколько отрицательных, то цепь заведомо неустойчивая и никаких дополнительных расчетов на устойчивость проводить не следует.

Несложный анализ показывает, что необходимое условие устойчивости - положительность всех коэффициентов дифференциального уравнения - является и достаточным только для цепей первого и второго порядка.

Критерий Рауса-Гурвица особенно удобен для проверки устойчивости цепей с заданными параметрами, т.е. с известным дифференциальным уравнением цепи. Применение его в общем случае ограничено рядом присущих ему недостатков:

1. Критерий Рауса-Гурвица требует знания всех коэффициентов дифференциального уравнения цепи с замкнутой ОС, что крайне неудобно при экспериментальных исследованиях цепей, так как обычно характеристики цепей определяются из испытаний разомкнутой цепи.

2. Критерий Рауса-Гурвица позволяет только определить устойчива цепь или неустойчива. Однако он не позволяет определить, как следует изменить параметры цепи, чтобы сделать ее устойчивой (или неустойчивой).

3. Применение критерия Рауса-Гурвица для цепей высокого порядка связано со значительными математическими трудностями, особенно если необходимо получить буквенный результат.

Значительными достоинствами по сравнению с этим критерием обладают частотные критерии устойчивости, среди которых наибольшее распространение получил критерий Найквиста.

5 КРИТЕРИЙ УСТОЙЧИВОСТИ НАЙКВИСТА

Этот критерий впервые был разработан в 1932 г. американцем Найквистом для исследования работы усилителей с ООС. В 1938 г. советским инженером А.В. Михайловым была впервые показана возможность его применения для исследования устойчивости любых линейных цепей с ОС. Поэтому иногда этот критерий называют критерием Найквиста-Михайлова.

Критерий Найквиста определяет условия, которым должны удовлетворять частотные характеристики разомкнутой цепи для того, чтобы эта же цепь с замкнутой цепью ОС была устойчивой. Достоинством критерия Найквиста по сравнению с другими критериями является возможность исследования устойчивости цепей по их экспериментально снятым частотным характеристикам, не имея дифференциальных уравнений цепей.

Применение критерия Найквиста наиболее целесообразно в тех случаях, когда размыкание цепи обратной связи приводит к значительному упрощению задачи исследования устойчивости цепи.

Рассмотрим физическую сущность вопроса устойчивости цепей на основе анализа их частотных характеристик и, используя полученные выводы, сформулируем критерий Найквиста.

Разомкнем в усилителе цепь ОС (рисунок 1). Тогда коэффициент передачи схемы с разомкнутой обратной связью, очевидно, равен

Рисунок 1

,

т.e. модуль и аргумент коэффициента передачи являются функциями частоты.

Параметры усилителя и четырехполюсника ОС могут быть подобраны так, чтобы . Тогда при замкнутой цепи ОС в схеме возможно существование колебаний даже при отсутствии источника внешнего возбуждения.

Действительно, появившееся на входе усилителя (вследствие флуктуации, коммутаций и т.п.) колебание не исчезает со временем, а после прохождения через цепь с ОС вновь появляется на входе, как бы восстанавливается за счет ОС. Усилитель становится генератором.

Очевидно, что равенство выполняется при условии:

. (7)

Соотношение (7) называют условием стационарности автоколебательного процесса генератора. С учетом комплексности величин и последнее равенство распадается на два:

(8)

Эти два равенства известны под названием условий баланса амплитуд и баланса фаз генератора. Первое условие определяет необходимую глубину ОС схемы, второе - сдвиг фаз ПОС, т.е. связь, поддерживающую внешнее воздействие.

В реальных генераторах автоколебания возникают при , когда незначительные флуктуации тока в активном элементе за счет ПОС лавинообразно нарастают, достигая установившихся значений. При этом в процессе установления стационарной амплитуды колебаний указанное неравенство переходит в равенство. Это происходит потому, что с ростом амплитуды колебаний активный элемент генератора работает все более в нелинейном режиме, а это приводит к уменьшению его коэффициента усиления .

Условия баланса амплитуд и фаз позволяют сформулировать условия устойчивости цепей с ОС на основе анализа их АЧХ и ФЧХ.

Если при изменения частоты от 0 до фазовый сдвиг не достигает величины , то цепь с замкнутой ОС устойчива при любой величине . С другой стороны, если на любой частоте , то цепь устойчива при любой ФЧХ. Система неустойчива, если имеются частоты, на которых одновременно выполняются два условия:

,

где

Вычисление АЧХ и ФЧХ для усилителя с разомкнутой цепью ОС обычно не представляет большой сложности. Построив графики и в функции от частоты, можно получить наглядное представление об устойчивости усилителя с замкнутой цепью ОС.

Пример указанных графиков для устойчивой цепи с ОС показан на рисунке 2,а, а для неустойчивой на рисунке 2,б.

На графиках АЧХ учтено, что величина при и в обычных усилителях, как правило, обращается в нуль. При это обусловлено влиянием разделительных конденсаторов в канале усилителя или ЧОС, а при влиянием шунтирующих паразитных емкостей (междуэлектродные емкости ламп и транзисторов, емкости монтажа и т.д.). В усилителях постоянного тока, не содержащих разделительных конденсаторов, при величина может принимать конечное значение.

а) б)

Рисунок 2

Рисунок 3

Приведенное выше условие устойчивости формулируется более сжато, если представить комплексный коэффициент передачи разомкнутой цепи на комплексной плоскости в полярной системе координат. В этой системе координат коэффициент передачи изобразится в виде вектора длиной , проведенного под углом к оси действительных чисел (рисунок 3). При изменении частоты конец этого вектора описывает кривую, называемую годографом амплитудно-фазовой характеристики (АФХ). При наличии в замкнутом кольце ОС разделительных конденсаторов и шунтирующих емкостей , как отмечалось выше, при и обращается в нуль. Поэтому для подобных усилителей годограф АФХ при изменении частоты от 0 до начинается и заканчивается в начале координат.

Предположим, что при некотором значении частоты фазовый сдвиг достигает величины , но цепь все же остается устойчивой. Для этого, очевидно, необходимо, чтобы на частоте .

Это означает, что вектор на частоте возможной генерации направлен по действительной оси, а отсекаемый годографом АФХ отрезок положительной действительной оси для устойчивой цепи должен быть меньше единицы. Если же этот отрезок превышает , т.е. , то все необходимые для генерации условия выполняются, и цепь неустойчива.

Отсюда и вытекает критерий устойчивости Найквиста: если годограф АФХ системы с разомкнутой цепью ОС не охватывает точку с координатами [l, 0], то данная система с замкнутой цепью ОС устойчива. В противном случае система неустойчива.

Примеры диаграмм Найквиста для устойчивой и неустойчивой системы приведены на рисунке 4. Стрелками показано направление, соответствующее увеличению частоты .

Рисунок 4