8

РОСТОВСКИЙ ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ СЕРВИСА И ТУРИЗМА

Южно-Российский государственный университет экономики и сервиса

____________________________________________________________________

Кафедра Радиоэлектроники

Лазаренко С.В.

ЛЕКЦИЯ № 16

ФИЛЬТР ВИНЕРА

по дисциплине “Радиотехнические цепи и сигналы”

г. Ростов-на-Дону

2012 г.

ЛЕКЦИЯ 16

ФИЛЬТР ВИНЕРА

Вопросы: 1 Постановка задачи фильтрации

2 Интегральное уравнение оптимального фильтра

3 Коэффициент передачи оптимального фильтра

В данной лекции реализуются следующие элементы квалификационной характеристики:

1 Студент должен знать временные и спектральные характеристики детерминированных сигналов.

2 Студент должен уметь использовать методы спектрального и корреляционного анализа детерминированных и случайных сигналов.

3 Студент должен владеть приемами измерения основных параметров и характеристик радиотехнических цепей и сигналов.

1 ПОСТАНОВКА ЗАДАЧИ ФИЛЬТРАЦИИ

Согласованный фильтр предполагает, что сигнал полностью известен. Как уже говорилось, с его помощью решается задача обнаружения сигнала на фоне помех. Время наблюдения при этом не должно быть меньше длительности сигнала.

После обнаружения возникает задача обработки этого сигнала с целью извлечения заложенной в нем информации. Если параметры сигнала за время наблюдения не изменяются, то обработка сводится к оценке этих параметров.

Однако существует целый класс задач, в которых параметры сигнала за время наблюдения существенно меняются. В этом случае задача оценки параметров переходит в задачу фильтрации.

При решении задачи оценки, так же, как и при фильтрации предполагается, что оцениваемый или фильтруемый параметр является случайным процессом.

Например, пусть на вход приемника поступает смесь амплитудно-модулированного сигнала

и помехи , т.е.

.

За время наблюдения параметр сигнала , несущий информацию, изменяется существенно. Задача приемника состоит в наилучшем воспроизведении реализации сигнала . Но это возможно с абсолютной точностью только в отсутствие помех. В реальных условиях приемник выдает так называемую оценку реализации сигнала, которая естественно отличается от реализации .

Сформулируем задачу фильтрации в следующем виде. На вход некоторой системы (фильтра) поступает аддитивная смесь полезного сигнала и шума (помехи)

.

Сигнал и шум являются независимыми эргодическими нормальными случайными процессами с известными корреляционными функциями , и равными нулю математическими ожиданиями.

Желаемым выходом фильтра является, естественно, сигнал

.

Реакцией реального фильтра является оценка сигнала, т.е.

.

Требуется найти характеристики реального фильтра, выходное колебание которого отличалось бы от желаемого выхода с минимальной среднеквадратической погрешностью

, (1)

где - символ усреднения.

Так как рассматриваемые процессы эргодические, то усреднение сводится к интегрированию (низкочастотной фильтрации).

Данная постановка задачи иллюстрируется следующей структурной схемой (рисунок 1).

Рисунок 1

Задача может ставиться несколько иначе: по известным значениям в прошлом и настоящем дать оптимальную оценку , т.е. в будущем.

2 ИНТЕГРАЛЬНОЕ УРАВНЕНИЕ ОПТИМАЛЬНОГО ФИЛЬТРА

Более подробно рассмотрим выражение (1). При этом учтем, что выходной сигнал искомого реального фильтра определится интегралом Дюамеля

, (2)

где - импульсная характеристика искомого реального фильтра.

Для нахождения этой характеристики определим квадрат ошибки

. (3)

Усредняя левую и правую части выражения (3), получим

. (4)

Учтем, что - энергия (дисперсия) сигнала ,

- взаимная корреляционная функция сигнала и принятого сигнала (принятой реализации) ,

- автокорреляционная функция принятого сигнала.

С учетом этого выражение (4) перепишется в виде

. (5)

Из выражения (5) необходимо найти такую импульсную характеристику , которая обеспечит минимум среднего значения квадрата ошибки фильтрации . Для решения этой задачи используем методы вариационного исчисления.

Предположим, что известна, и соответствующая ей ошибка минимальна, т.е. . Тогда любая другая импульсная характеристика только увеличивает значение ошибки.

Пусть импульсная характеристика какого-то условного фильтра равна

, (6)

где - произвольная функция, не равная тождественно нулю;

- любое число.

Найдем среднеквадратическую ошибку фильтрации этого условного фильтра, для чего подставим в выражение (5) соотношение (6).

. (7)

Очевидно, что при ошибка фильтрации минимальна, так как в этом случае .

Перепишем формулу (7) в следующем виде

. (8)

Согласно выражению (5)

. (9)

Введем обозначения

, (10)

. (11)

Подставляя соотношения (9), (10), (11) в выражение (8), получим

. (12)

Теперь в общем случае необходимо подобрать так, чтобы минимизировать выражение (12). Условие минимума

,

откуда следует

. (13)

С другой стороны, как было отмечено ранее, для обеспечения минимума , необходимо, чтобы . Из выражения (13) следует, что .

Преобразуем выражение (10) следующим образом, поменяв порядок интегрирования и приравняв

.

Так как функция - произвольная функция, не равная нулю, то, следовательно, нулю равно выражение в квадратных скобках, откуда следует:

. (14)

Интегральное уравнение (14), называемое уравнением Винера-Хопфа, определяет оптимальную импульсную характеристику искомого фильтра.

3 КОЭФФИЦИЕНТ ПЕРЕДАЧИ ОПТИМАЛЬНОГО ФИЛЬТРА

При определении коэффициента передачи оптимального фильтра Винера учтем следующее обстоятельство. Взаимная корреляционная функция сигнала и принятого сигнала (принятой реализации) , определяемая выражением (14), есть свертка оптимальной импульсной характеристики и автокорреляционной функции принятого сигнала.

Применяя к обеим частям выражения (14) преобразование Фурье и используя свойства спектра свертки двух функций, получим

, (15)

где - взаимный энергетический спектр сигнала и принятой реализации (смеси сигнала и шума);

- коэффициент передачи мощности оптимального фильтра;

- энергетический спектр принятой реализации (смеси сигнала и шума).

Из выражения (15) следует

. (16)

Если сигнал и помеха не коррелированны между собой (что практически всегда выполняется), то

,

,

где - спектральная плотность мощности помехи (шума).

В этом случае выражение (16) приобретает вид

. (17)

Анализ выражения (17) показывает, что в случае, когда спектры сигнала и помехи не пересекаются, то коэффициент передачи мощности оптимального фильтра в пределах полосы частот, занимаемой сигналом, есть величина постоянная. Когда же спектры пересекаются, то значение коэффициента передачи меньше на тех частотах, где уровень спектральной плотности мощности шума выше. Сказанное иллюстрируется рисунками 2 и 3.

Рисунок 2

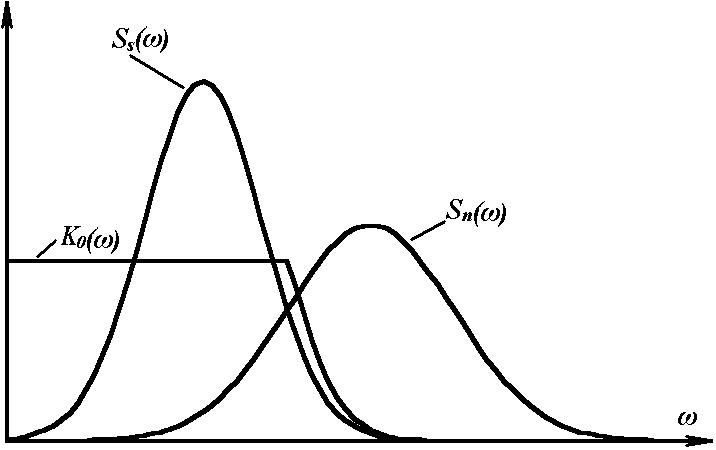
Рисунок 3

Среднеквадратическая ошибка восстановления сигнала с помощью оптимального фильтра определится на основании уравнения Винера-Хопфа при

,

где и - нижняя и верхняя частотные границы фильтра.

Лекцию подготовил старший преподаватель С. Лазаренко