12

РОСТОВСКИЙ ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ СЕРВИСА И ТУРИЗМА

Южно-Российский государственный университет экономики и сервиса

____________________________________________________________________

Кафедра Радиоэлектроника

Лазаренко С.В.

ЛЕКЦИЯ № 24

ЦИФРОВЫЕ ФИЛЬТРЫ

по дисциплине “Радиотехнические цепи и сигналы”

Ростов-на-Дону

2011

ЛЕКЦИЯ 24

ЦИФРОВЫЕ ФИЛЬТРЫ

по дисциплине ”Радиотехнические цепи и сигналы”

Изучаемые вопросы: 1 Трансверсальный цифровой фильтр

2 Рекурсивный цифровой фильтр

1 ТРАНСВЕРСАЛЬНЫЙ ЦИФРОВОЙ ФИЛЬТР

Физически осуществимые цифровые фильтры, которые работают в реальном масштабе времени, для формирования выходного сигнала в -тый дискретный момент времени могут использовать следующие данные:

1) значение входного сигнала в момент -того отсчета, а также некоторое число "прошлых" входных отсчетов , , ..., ;

2) некоторое число предшествующих отсчетов выходного сигнала , , ..., .

Целые числа и определяют порядок ЦФ. В зависимости от того, как используется информация о прошлых состояниях системы ЦФ делятся на трансверсальные и рекурсивные. Рекурсивные фильтры будут рассмотрены в следующей лекции. В рамках же данной лекции рассмотрим трансверсальные фильтры.

Так принято называть фильтры, не использующие для формирования выходного сигнала в -тый момент времени его предыдущие отсчеты, т.е. фильтры, работающие в соответствии с алгоритмом:

, (1)

где , ,…, - последовательность коэффициентов (например, отсчеты импульсной характеристики фильтра).

Число является порядком трансверсального ЦФ. Как видно из формулы (1), трансверсальный фильтр производит взвешенное суммирование предшествующих отсчетов входного сигнала и не использует прошлые отсчеты выходного сигнала. Таким образом, этот фильтр, не охвачен обратной связью.

Применив -преобразование к обеим частям выражения (1), получим

Отсюда следует, что системная функция трансверсального равна

. (2)

Системная функция трансверсального цифрового фильтра есть дробно-рациональная функция аргумента , имеющей -кратный полюс при и нулей, координаты которых определяются коэффициентами фильтра.

Алгоритм функционирования трансверсального ЦФ поясняется структурной схемой, приведенной на рисунке 1.

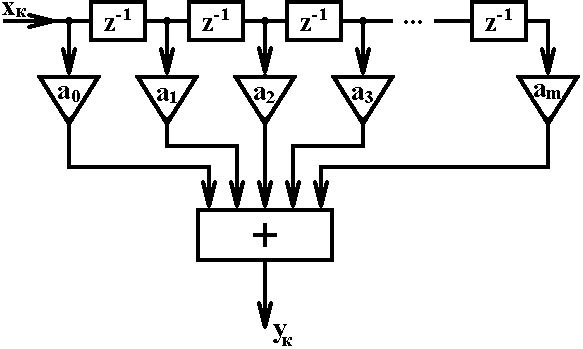
Рисунок 1

Основными элементами фильтра служат блоки задержки отсчетных значений на один интервал дискретизации (прямоугольники с символами ), a также масштабные блоки, выполняющие в цифровой форме операции умножения на соответствующие коэффициенты. С выходов масштабных блоков сигналы поступают в сумматор, где, складываясь, образуют отсчет выходного сигнала.

Получить выражение для комплексного коэффициента передачи трансверсального фильтра можно на основании выражения (2), поскольку связь между z-преобразованием и преобразованием Фурье уже была рассмотрена ранее. Комплексный коэффициент передачи цифрового фильтра получается из системной функции заменой аргумента на . Следовательно, получим:

.

При заданном шаге дискретизации можно реализовать самые разнообразные формы частотных характеристик, подбирая должным образом весовые коэффициенты фильтра.

На основе задания комплексного коэффициента передачи может быть реализован один из алгоритмов цифровой фильтрации непрерывного сигнала:

1) производится дискретизация непрерывного входного сигнала;

2) определяется дискретное преобразование Фурье (в том числе с использованием алгоритма быстрого преобразования);

3) перемножением комплексных коэффициентов дискретного ряда Фурье входного сигнала и значений комплексного коэффициента передачи цифрового фильтра определяется дискретное преобразование выходного сигнала;

4) путем использования обратного дискретного преобразования Фурье определяется выходная последовательность, которая затем может быть преобразована в непрерывный сигнал.

Импульсная характеристика цифрового фильтра, по определению, есть обратное -преобразование от системной функции. Поэтому опять используем формулу (2).

Из предыдущих лекций известно выражение для обратного -преобразования:

. (7)

Прямая подстановка системной функции трансверсального цифрового фильтра (2) в выражение (7) с учетом соотношений (4)...(6) дает следующий результат:

.

Важно отметить, что импульсная характеристика трансверсального цифрового фильтра содержит конечное число членов.

Следует иметь в виду, что схема, изображенная на рисунке 1, не является принципиальной электрической схемой цепи, а служит лишь графическим изображением алгоритма обработки сигнала. Этот алгоритм наглядно иллюстрируется рисунком 2.

Нулевой такт Первый такт

Второй такт Третий такт

Рисунок 2

Из рассмотрения рисунков видно, что

,

,

,

и т.д.

В общем случае

. (9)

Выражение (9) и определяет алгоритм, который может быть запрограммирован на одном из алгоритмических языков. Составим фрагмент программы, используя для этого язык Паскаль.

Предположим, что импульсная характеристика трансверсального фильтра задана массивом из чисел. Пусть входной сигнал проставлен массивом также из чисел. Тогда программа формирования выходного сигнала будет иметь вид:

В первой строке задается цикл по индексу , в котором обнуляются все начальные значения выходной последовательности. Внутри этого цикла задается второй цикл по индексу , в котором и вычисляются значения выходной последовательности. Убедимся в этом.

1) при , может быть только 0.

2) при и при , следовательно,

при , значит,

3) при и при , следовательно, ,

при , значит, ,

при , значит,

и т.д.

Рассмотренная программа может быть реализована на персональной ЭВМ, причем, входной сигнал в цифровой форме может поступать на обработку через последовательный порт. Чтение отсчетов входного сигнала при этом необходимо осуществлять в цикле по .

Трансверсальный фильтр первого порядка

Схема этого фильтра приведена на рисунке 3

Рисунок 3

Входная последовательность фильтра определяется выражением

Следовательно, импульсная характеристика равна

.

Системная функция такого фильтра

,

а комплексный коэффициент передачи

.

Очень просто найти выражение для АЧХ фильтра.

При получаем

.

На частоте АЧХ обращается в нуль, и данный фильтр может выступать в качестве режекторного.

При имеем

,

и фильтр становится полосовым, средняя частота которого равна .

2 РЕКУРСИВНЫЙ ЦИФРОВОЙ ФИЛЬТР

Рекурсивный цифровой фильтр характерен тем, что для формирования -того выходного отсчета используются предыдущие значения не только входного, но и выходного сигнала:

. (1)

При этом коэффициенты , определяющие рекурсивную часть алгоритма фильтрации, не равны нулю одновременно.

Преобразуем уравнение (1), сгруппировав отсчеты выходного сигнала слева, входного - справа:

. (2)

Найдем -преобразование от обеих частей уравнения

. (3)

и получим выражение для системной функции рекурсивного цифрового фильтра

. (4)

Системная функция имеет на -плоскости полюсов. Если коэффициенты рекурсивной части алгоритма вещественны, то эти полюсы либо лежат на вещественной оси, либо образуют комплексно-сопряженные пары.

Структурная схема алгоритма вычислений, проводимых в соответствии с формулой (1), приведена на рисунке 1.

Рисунок 1

Верхняя часть структурной схемы отвечает трансверсальной (нерекурсивной) части алгоритма фильтрации. Для ее реализации в общем случае требуется масштабных блоков и ячеек памяти, в которых хранятся входные отсчеты.

Рекурсивной части алгоритма соответствует нижняя часть структурной схемы. Здесь используются последовательных значений выходного сигнала, которые в процессе работы фильтра перемещаются из ячейки в ячейку путем сдвига.

Рисунок 2

Недостатком данного принципа реализации является потребность в большом числе ячеек памяти, отдельно для рекурсивной и нерекурсивной частей. Более совершенны канонические схемы рекурсивных ЦФ, в которых используется минимально возможное количество ячеек памяти. Число ячеек равно наибольшему из чисел и . В качестве примера на рисунке 2 изображена структурная схема канонического рекурсивного фильтра 2-го порядка, которой отвечает системная функция

. (5)

Для того, чтобы убедиться, что эта система реализует заданную функцию, рассмотрим вспомогательный дискретный сигнал на выходе первого сумматора и запишем два очевидных соотношения:

. (6)

Выполнив -преобразование выражений (6), получим

. (7)

Объединив соотношения (7), получим формулу (5)

Характерная черта, отличающая рекурсивный цифровой фильтр, состоит в том, что из-за наличия обратной связи его импульсная характеристика имеет вид неограниченно-протяженной последовательности. Покажем это на примере простейшего фильтра первого порядка, системная функция которого описывается выражением

.

Импульсная характеристика, как известно, есть обратное - преобразование от системной функции, поэтому можно записать

.

Вначале найдем :

.

Произведя замену , получим

.

Аналогично найдем

.

Не трудно убедиться в том, что , и т.д. Искомая импульсная характеристика представляет собой геометрическую прогрессию. Очевидно, что для того, чтобы прогрессия была убывающей (чтобы фильтр был устойчивым), необходимо выполнения условия .

Комплексный коэффициент передачи рекурсивного цифрового фильтра первого порядка получим на основе системной функции (14) путем замены на :

Отсюда не трудно найти АЧХ

.

В зависимости от коэффициента АЧХ может быть различной.

Лекцию подготовил старший преподаватель кафедры С. Лазаренко