4. Линейные функции случайных величин.

Пусть - нормально распределенная случайная величина с параметрамии. Тогда,если A и B - постоянные, то случайная величина , линейно зависящая от , также нормально распределена, причем *

Докажем это утверждение. Пусть для простоты B>0. Оценим вероятность неравенств 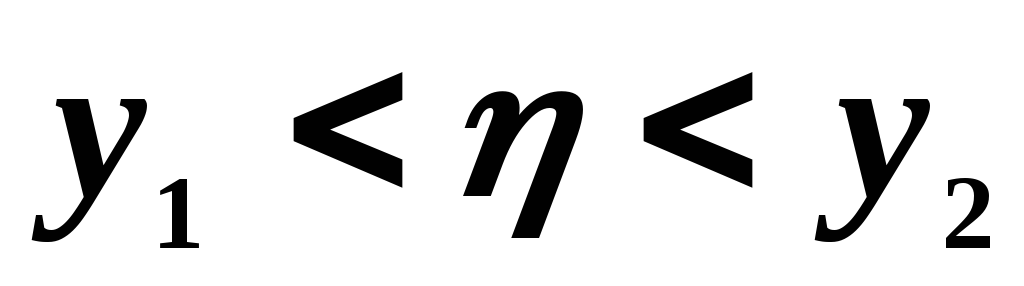. Ясно, что эти неравенства равносильны неравенствам, т.е.

Поэтому

Так как величина 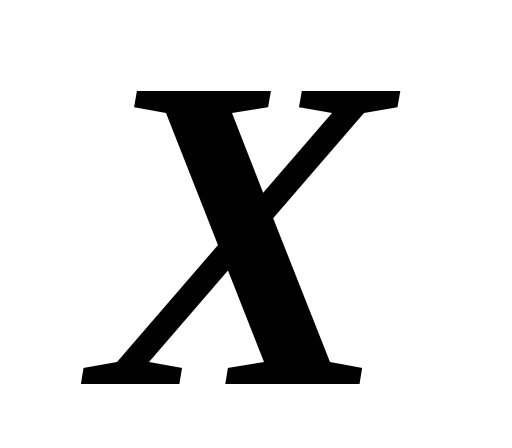распределена нормально, то

Проведем в этом интеграле замену переменной, полагая . Тогдаи, следовательно,

Итак,

 Это равенство показывает, что случайная величина имеет нормальное распределение, причем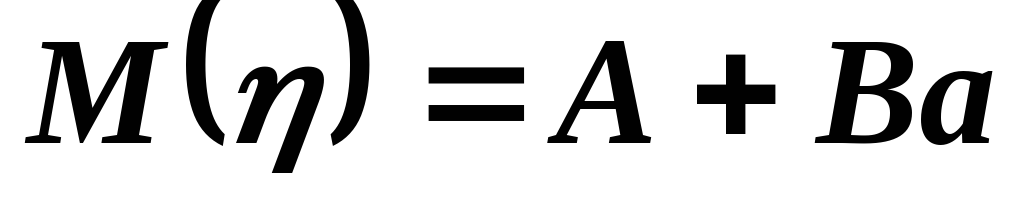и.

Имеет место и более общее утверждение. Пусть - постоянные, а- нормально распределенные попарно независимые случайные величины, причем.

Тогда случайная величина

также имеет нормальное распределение, причем

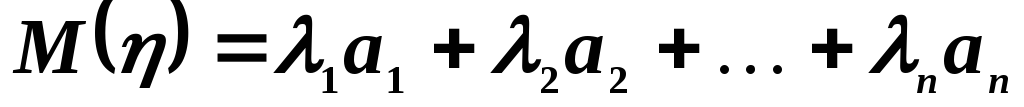
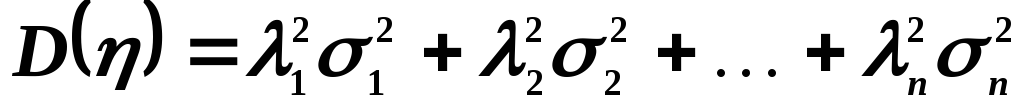
В частности, если при любом i, то случайная величина распределена нормально, причем,,.

   * Это утверждение можно получить просто из свойств математического ожидания и дисперсии. Так, например,

FVB