
- •19 Vektor
- •2. Линейные операции над векторами.
- •Свойства линейных операций над векторами.
- •3. Понятие линейной зависимости векторов.
- •4. Понятие о проекциях.
- •Декартова система координат.
- •Связь компонент, проекций, направляющих косинусов и коэффициентов в разложении по базису.
- •Деление отрезка в данном отношении.
- •5. Линейные операции над векторами, заданными своими координатами.
- •5.А. Скалярное произведение векторов.
- •Свойства скалярного произведения.
- •5.Б. Векторное произведение.
- •Векторное произведение двух векторов, заданных своими проекциями.
- •Механический смысл векторного произведения.
- •Свойства векторного произведения векторов.
- •5.В. Смешанное произведение трех векторов.
- •Смешанное произведение векторов, заданных своими координатами.
- •Свойства смешанного произведения.
Свойства скалярного произведения.
Скалярное произведение двух ненулевых векторов равно нулю тогда и только тогда, когда векторы ортогональны:
 .
.Скалярное произведение коммутативно:
 .
.Скалярное произведение ассоциативно относительно скалярного множителя:
 .
.Скалярное произведение дистрибутивно:
![]() .
.
Свойство скалярного квадрата:
 ,
отсюда
,
отсюда .
.
Рассмотрим таблицу скалярного умножения ортов:
![]()
![]()
Скалярное произведение одноименных ортов равно единице, а разноименных - нулю.
Угол между двумя векторами.
Из определения скалярного произведения:
![]()
 .
.
Условие ортогональности двух векторов:
![]()
Условие коллинеарности двух векторов:
![]() .
.
Следует
из определения 5 -
![]() .
Действительно, из определения произведения
вектора на число, следует
.
Действительно, из определения произведения
вектора на число, следует![]() .
Поэтому, исходя из правила равенства
векторов, запишем
.
Поэтому, исходя из правила равенства
векторов, запишем![]() ,
,![]() ,
,![]() ,
откуда вытекает
,
откуда вытекает![]() .
Но вектор
.
Но вектор![]() ,
получившийся в результате умножения
вектора
,
получившийся в результате умножения
вектора![]() на число
на число![]() ,
коллинеарен вектору
,
коллинеарен вектору![]() .
.
Проекция вектора на вектор:
 .
.
Пример 4.
Даны
точки
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Найти скалярное произведение
![]() .
.
Решение.
![]() найдем по формуле скалярного произведения
векторов, заданных своими координатами.
Поскольку
найдем по формуле скалярного произведения
векторов, заданных своими координатами.
Поскольку
![]() ,
,![]() ,
,
![]() ,
,![]()
то
![]() .
.
Пример 5. Даны
точки
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Найти проекцию
![]() .
.
Решение. Поскольку
![]() ,
,![]() ,
,
![]() ,
,![]()
то
![]() и
и
![]() .
.
На основании формулы проекции, имеем
![]() .
.
Пример 6. Даны
точки
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Найти угол между векторами
![]() и
и![]() .
.
Решение. Заметим, что вектора
![]() ,
,![]() ,
,
![]() ,
,![]()
не являются коллинеарными, поскольку не пропорциональны их координаты:
![]() .
.
Эти вектора не являются
также перпендикулярными, так как их
скалярное произведение
![]() .
.
Найдем
![]() ,
,![]()
Угол
![]() найдем из формулы:
найдем из формулы:
![]() .
.
Пример 7.
Определить при каких
![]() вектора
вектора![]() и
и![]() коллинеарны.
коллинеарны.![]()
Решение.
В случае коллинеарности, соответствующие
координаты векторов
![]() и
и![]() должны быть пропорциональны, то есть:
должны быть пропорциональны, то есть:
![]() .
.
Отсюда
![]() и
и![]() .
.
Пример 8.
Определить, при каком значении
![]() вектора
вектора![]() и
и![]() перпендикулярны.
перпендикулярны.
Решение.
Вектора
![]() и
и![]() перпендикулярны, если их скалярное
произведение
перпендикулярны, если их скалярное
произведение![]() равно нулю. Из этого условия получаем:
равно нулю. Из этого условия получаем:![]() .
Стало быть,
.
Стало быть,![]() .
.
Пример 9.
Найти![]() ,
если
,
если
![]() ,
,
![]() ,
,
![]() .
.
Решение. В силу свойств скалярного произведения, имеем:

Пример
10.
Найдите угол между векторами
![]() и
и![]() ,
где
,
где
![]() и
и![]() - единичные
векторы и угол между векторами
- единичные
векторы и угол между векторами
![]() и
и![]() равен 120о.
равен 120о.
Решение.
Имеем:
![]() ,
,![]() ,
,
![]()
![]()
![]()
Значит
![]()
![]()
![]()
Значит
![]()
Окончательно
имеем:
![]() .
.
5.Б. Векторное произведение.
Определение
21.
Векторным
произведением
вектора
![]() на вектор
на вектор![]() называется вектор
называется вектор![]() ,
или
,
или![]() ,
определяемый следующими тремя условиями:
,
определяемый следующими тремя условиями:
Модуль вектора
 равен
равен ,
где
,
где -
угол между векторами
-
угол между векторами и
и ,
т.е.
,
т.е. .
.
Отсюда
следует, что модуль векторного произведения
численно равен площади параллелограмма,
построенного на векторах
![]() и
и![]() как на сторонах.
как на сторонах.
Вектор
 перпендикулярен к каждому из векторов
перпендикулярен к каждому из векторов и
и (
( ;
; ),
т.е. перпендикулярен плоскости
параллелограмма, построенного на
векторах
),
т.е. перпендикулярен плоскости
параллелограмма, построенного на
векторах и
и .
.Вектор
 направлен так, что если смотреть из
его конца, то кратчайший поворот от
вектора
направлен так, что если смотреть из
его конца, то кратчайший поворот от
вектора к вектору
к вектору был бы против часовой стрелки (векторы
был бы против часовой стрелки (векторы ,
, ,
, образуют правую тройку).
образуют правую тройку).
Векторное произведение двух векторов, заданных своими проекциями.
Пусть
даны векторы
![]() и
и![]() ,
тогда
,
тогда
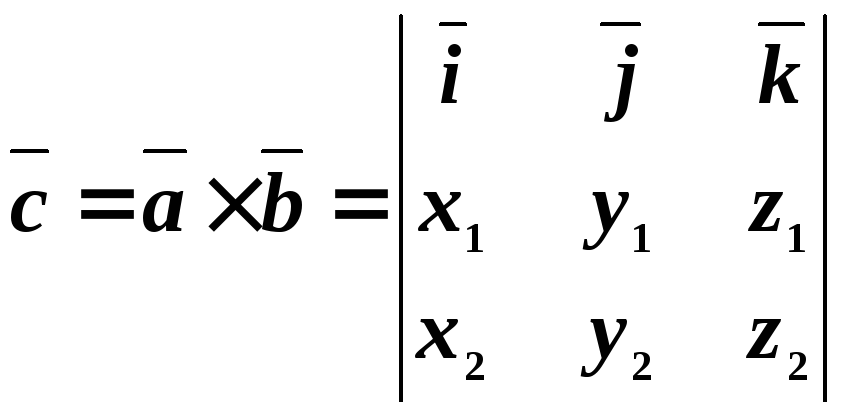 .
.
Если разложить определитель по элементам первой строки, то
![]() =
=![]() .
.
