
- •30 AnGeom
- •2. Прямая линия на плоскости
- •Типы уравнений прямой.
- •3. Угол между двумя прямыми. Условие параллельности и перпендикулярности.
- •Линейные образы в r3
- •4. Понятие алгебраической поверхности.
- •4.А. Плоскость.
- •5. Прямая линия в пространстве.
- •5.А. Канонические уравнения прямой в пространстве.
- •5.Б. Приведение общих уравнений прямой к каноническому виду.
- •6. Угол между двумя прямыми. За угол между двумя прямыми
- •7. Прямая и плоскость.
- •Условие того, что прямая лежит в данной плоскости.
- •Условие того, что две прямые лежат в одной плоскости.
- •8. Кривые второго порядка.
- •8.А Окружность
- •8.Б. Эллипс (в декартовой системе координат)
- •8.В. Гипербола
- •Каноническое уравнение гиперболы
- •8.Г. Парабола
- •Пример 18. Установить, что уравнение
- •Полярная система координат.
- •Связь между прямоугольными и полярными координатами.
Условие того, что две прямые лежат в одной плоскости.
Пусть имеем две прямые:
![]() и
и
![]() .
.
Отсюда,
направляющие вектора этих прямых
![]() ,
,![]() и точки
и точки![]() ,
,![]() лежат на соответствующих прямых. Если
прямые лежат в одной плоскости, то
векторы
лежат на соответствующих прямых. Если
прямые лежат в одной плоскости, то
векторы![]()
![]() и
и![]() 2
компланарны. Условие того, что две прямые
лежат в одной плоскости равносильно
условию компланарности этих векторов:
2
компланарны. Условие того, что две прямые
лежат в одной плоскости равносильно
условию компланарности этих векторов:
![]() или
или
 .
(32)
.
(32)
Условие (32) является также критерием пересечения двух прямых.
Замечание. Если заданы две прямые, то они могут быть в одном из трех следующих соотношений:
п
 араллельны,
араллельны,

 ,
,пересекаются,


прямые (1) и (2) скрещиваются (рис. 12), следовательно,
 .
Тогда возникает вопрос об определении
расстояния между скрещивающимися
прямыми, как высоты параллелепипеда,
построенного на векторах
.
Тогда возникает вопрос об определении
расстояния между скрещивающимися
прямыми, как высоты параллелепипеда,
построенного на векторах ,
как на сторонах:
,
как на сторонах:
![]()
 .
.
Пример
8.
Найти уравнение плоскости, проходящей
через точку
![]() параллельно прямым :
параллельно прямым :
![]() :
:
![]() и
и![]() :
:
 .
.
Решение.
На
искомой плоскости образуем текущий
вектор
![]() .
Из канонического уравнения прямой
.
Из канонического уравнения прямой
![]() и параметрического уравнения прямой
и параметрического уравнения прямой
![]() получим координаты их направляющих
векторов
получим координаты их направляющих
векторов![]() и
и![]() .
Условие компланарности этих трех
векторов
.
Условие компланарности этих трех
векторов![]() дает уравнение плоскостиα:
дает уравнение плоскостиα:
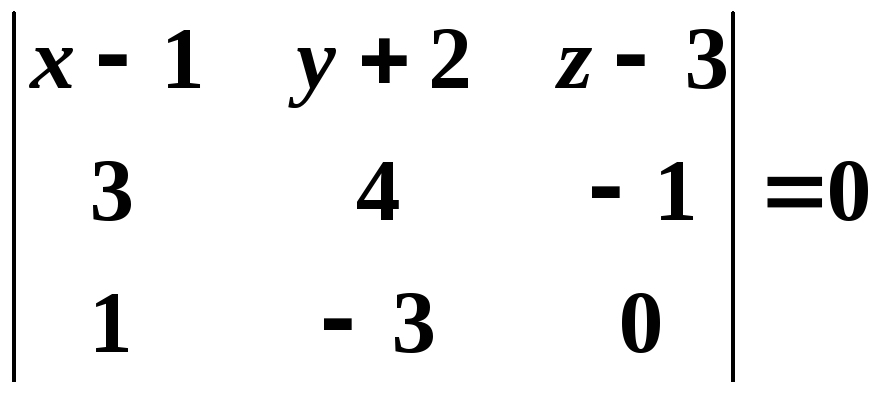 .
.
Пример
9.
Найти уравнение плоскости, проходящей
через точку
![]() и прямую
и прямую![]() :
:
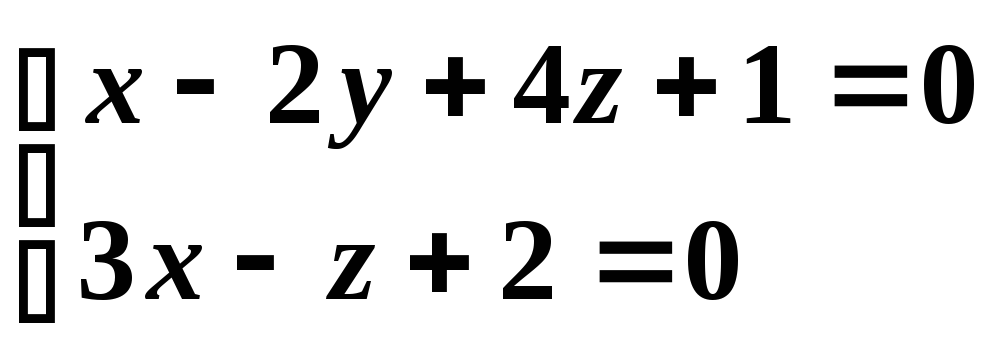 .
.
Решение.
На
искомой плоскости образуем текущий
вектор
![]() .
.
Уравнение
прямой задано пересечением плоскостей,
поэтому ее направляющий вектор
![]() определяется из равенств:
определяется из равенств:
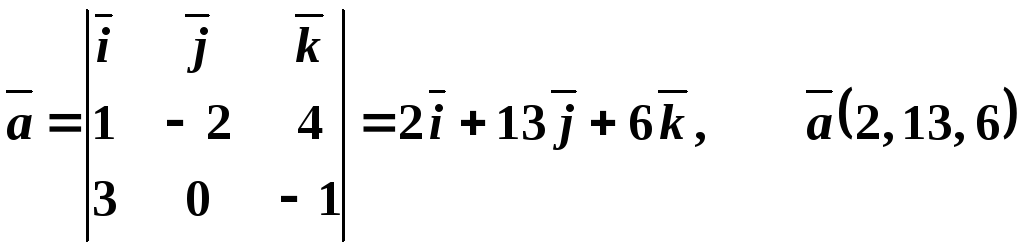 .
.
Так
как
![]() ,
,
![]() ,
то
,
то
![]() .
.
На
прямой
![]() зафиксируем произвольную точку
зафиксируем произвольную точку![]() .
Координаты
.
Координаты![]() найдем из системы уравнений заданной
прямой, положив в них, например,
найдем из системы уравнений заданной
прямой, положив в них, например,![]() :
:
 .
.
Решая
эту систему, получим
![]() ,
,![]() .
Таким образом,
.
Таким образом,![]() .
Соединив точки
.
Соединив точки![]() и
и![]() ,
получим вектор
,
получим вектор![]() ,
принадлежащий плоскостиα.
,
принадлежащий плоскостиα.
Для
любой точки
![]() выполняется условие компланарности
векторов
выполняется условие компланарности
векторов![]() .
И, так как
.
И, так как
![]() не
параллелен
не
параллелен
![]() ,
то уравнение плоскости дается равенством:
,
то уравнение плоскости дается равенством:

Пример 10. Найти уравнение плоскости α, проходящей через прямые
![]() :
:
![]() и
и![]() :
:![]() .
.
Решение.
Из
канонического уравнения прямой
![]() найдем координаты некоторой точки
найдем координаты некоторой точки
![]() ,
расположенной на
,
расположенной на
![]() :
:
![]() и, соединив ее с текущей точкой
и, соединив ее с текущей точкой![]() ,
образуем текущий вектор
,
образуем текущий вектор![]() .
.
Из
уравнений прямых получим направляющие
вектора
![]() ,
,![]() ,
которые, как и прямые
,
которые, как и прямые
![]() ,
,
![]() ,
принадлежат плоскости
,
принадлежат плоскости
![]() . Так как для любой точки
. Так как для любой точки
![]() выполняется условие компланарности
векторов
выполняется условие компланарности
векторов![]() ,
а
,
а![]() не параллелен
не параллелен![]() 2,
то искомая плоскость описывается
уравнением:
2,
то искомая плоскость описывается
уравнением:

Остальные семь примеров в другом файле.
8. Кривые второго порядка.
Порядком алгебраического уравнения называется высшая степень входящего в уравнение неизвестного. Порядок кривой не зависит от выбора осей координат на плоскости.
Общий вид кривой 2-го порядка:
![]()
К кривым 2-го порядка относятся эллипс, частным случаем которого является окружность, гипербола и парабола.
8.А Окружность
Пусть
![]() – центр окружности радиуса
– центр окружности радиуса![]() ,
тогда уравнение окружности имеет вид:
,
тогда уравнение окружности имеет вид:
![]()
8.Б. Эллипс (в декартовой системе координат)
Э ллипсом
называется множество точек плоскости,
сумма расстояний от которых до двух
данных точек, называемых фокусами
эллипса, постоянна и равна
ллипсом
называется множество точек плоскости,
сумма расстояний от которых до двух
данных точек, называемых фокусами
эллипса, постоянна и равна![]() (рис. 13).
(рис. 13).
Пусть
фокусами эллипса являются точки
![]() и
и![]() ,
при этом
,
при этом![]() есть фокальная ось эллипса.
есть фокальная ось эллипса.![]() – некоторая точка, принадлежащая
эллипсу. По определению эллипса, для
любой его точки
– некоторая точка, принадлежащая
эллипсу. По определению эллипса, для
любой его точки![]() ,
имеем:
,
имеем:
![]()
Пусть
ось
![]() совпадает с фокальной осью
совпадает с фокальной осью![]() .
Начало координат выберем посередине
между фокусами
.
Начало координат выберем посередине
между фокусами![]() и
и![]() ,
а ось
,
а ось![]() перпендикулярно фокальной оси. При
таком выборе системы координат уравнение
эллипса примет вид:
перпендикулярно фокальной оси. При
таком выборе системы координат уравнение
эллипса примет вид:
![]() .
.
Действительно,
согласно рисунку 13,
![]() .
Следовательно,
.
Следовательно,![]() .
.
Аналогично
![]() .
Отсюда, по определению,
.
Отсюда, по определению,
![]()
Преобразуем полученное уравнение эллипса.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Отсюда получаем искомое уравнение эллипса.
Так
как из
![]() следует, что
следует, что![]() т.е.
т.е.![]() ,
то полагают
,
то полагают![]() и получаютканоническую
(простейшую) форму
уравнения эллипса:
и получаютканоническую
(простейшую) форму
уравнения эллипса:
![]()
 .
(33)
.
(33)
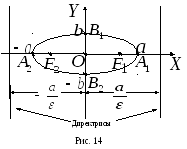
Эксцентриситет
эллипса:
![]() .
.
![]()
 –вершины
эллипса, a
директрисы имеют уравнения:
–вершины
эллипса, a
директрисы имеют уравнения:
![]() (рис. 14).
(рис. 14).
Параметрические уравнения эллипса (рис. 15):
