2.6. Планы скоростей и ускорений кулисного механизма

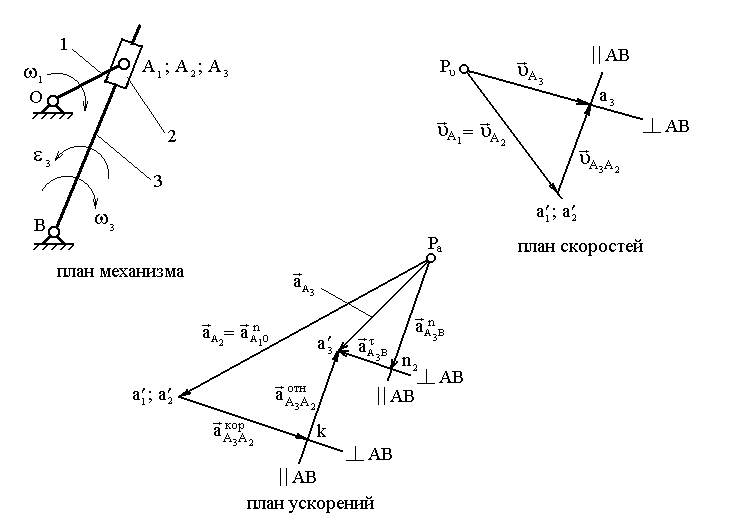
Рис. 2.5. Построение планов скоростей и ускорений кулисного механизма

Чтобы построить план скоростей, необходимо составить векторное уравнение скоростей. При этом следует иметь в виду, что точка А₁, принадлежащая кривошипу 1, и точка А₂, принадлежащая ползуну 2 и совпадающая на плане механизма с точкой А₁, вращаются вокруг оси О с одинаковыми линейными и угловыми скоростями:

V_А1 = V_А2 и .

Если задана величина ₁, то величину линейной скорости рассчитывают по формуле:

V_А1 = V_А2 = ₁ L_ОА, м/с.

Векторы скоростей V_А1 и V_А2 направлены перпендикулярно радиусу ОА₁. Скорость точки А₃, принадлежащей кулисе 3, можно найти по следующему векторному уравнению скоростей:

V_А3 = V_А2 + V_А3А2 ,

где V_А3А2 – вектор скорости точки А₃ кулисы относительно точки А₂ ползуна; он перпендикулярен прямой А₁В плана механизма.

После выбора масштаба плана скоростей _v (см. предыдущие примеры механизмов) строят план скоростей в следующей последовательности.

Из полюса Р_v (рис.2.5) перпендикулярно отрезку ОА плана механизма, проводится вектор скорости V_А1 , совпадающий с вектором скорости V_А2 . На рис. 2.5 это вектор . Через точкуа₁ проводится прямая, параллельная прямой А₁В, а через полюс Р_v – прямая, перпендикулярная А₁В. На их пересечении получают точку а₃ и наносят направление векторов (“стрелки”), руководствуясь векторным уравнением скоростей.

Вычисляют величины скоростей:

, м/с;

, м/с.

где Р_va₃ и а₁а₃ – длины векторов, измеренные на плане скоростей.

Угловая скорость коромысла 3 вычисляется по формуле

,с^-1.

Для построения плана ускорений составляются следующие векторные уравнения:

а_А3 = а_А2 + а^кор_А3А2 + а^отн_А3А2 ,

а_А3 = а_В + аⁿ_А3В + а^_А3В,

где а_А2 – ускорение ползуна,

а^кор_А3А2 – Кориолисово ускорение точки А₃ относительно А₂ (возникает тогда, когда есть относительное движение двух точек с одновременным вращением их вокруг какой-либо оси; в данном случае точка А₃ движется относительно А₂, и вместе они вращаются вокруг неподвижной точки В); направление вектора а^кор_А3А2 определяется так – необходимо условно повернуть вектор скорости V_А3А2 по направлению вращения кулисы 3, это и будет направление Кориолисова ускорения;

а^отн_А3А2 - относительное ускорение точки А₃ относительно А₂; его вектор параллелен А₃В;

а_В - ускорение точки В; а_В = 0, так как точка В неподвижна;

аⁿ_А3В - нормальное ускорение точки А₃ относительно В; направление вектора – от А₃ к точке В;

а^_А3В - тангенциальное ускорение точки А₃ относительно В; вектор направлен перпендикулярно А₃В.

Вычисление величины Кориолисова и нормальных ускорений можно произвести по следующим формулам:

а_А2 = аⁿ_А1О = ²₁ L_ОА, м/с²;

а^кор_А3А2 = 2₃ V_А3А2, м/с²;

аⁿ_А3В = ²₃ L_А3В, м/с².

Выбирается масштаб плана ускорений с использованием формулы

,

где Р_аа₂ – длина вектора, изображающего ускорение а_А2 на плане ускорений; она выбирается произвольной длины с таким расчётом, чтобы, во-первых, будущий план ускорений разместился на отведённом месте чертежа, и, во-вторых, чтобы масштаб был удобен для использования в дальнейших расчётах (был “круглым числом”).

Остальные известные величины ускорений переводятся масштабом в векторные отрезки соответствующих длин

, мм;

, мм.

Затем строится план ускорений в следующей последовательности.

Из произвольно выбранного полюса – точки Р_а – проводится вектор ускорения аⁿ_А1О с длиной Р_аа₂^’. Из точки а₂^’перпендикулярно А₂В проводится вектор ускорения а^кор_А3А2 с длиной . Через точкуk проводится прямая, перпендикулярная к этому вектору. Таким образом, будет выполнено графическое изображение первого векторного уравнения ускорений из двух ранее составленных.

Затем приступают к построению второго векторного уравнения. Из полюса Р_а параллельно прямой А₃В проводится вектор ускорения аⁿ_А3В длиной Р_аn₂, и через точку n₂ – перпендикулярная ему прямая до пересечения с прямой, проведённой ранее через точку k. На пересечении этих прямых получается точка а₃^’. Вектор, соединяющий точки Р_а и а₃^’, есть полное ускорение а_А3 точки А₃.

Затем вычисляется угловое ускорение кулисы по формуле

, с^-2,

где n₂a₃^` – длина вектора, изображающего на плане ускорений тангенциальное ускорение точки А₃ .

Направление углового ускорения определяется, как и в предыдущем примере (для кривошипно-ползунного механизма), то есть по направлению условного вращения кулисы 3 вектором ускорения а^_А3В. При этом нужно условно перенести этот вектор в точку А₃ плана механизма и посмотреть, в каком направлении он будет «вращать» кулису.