Контрольная работа по математике №1 (утс)

Демонстрационный вариант.

Комплексные числа

1. . Найти.

2. . Найти.

3. . Найти модуль и аргумент комплексного числа.

4. . Записать в тригонометрической форме число.

5. . Найти.

6. . Найти.

Линейная алгебра

1. Даны матрицы и. Найти:

; ;;.

2. При каком значении определительравен нулю.

3. При каком значении матрицавырождена.

4. Решить систему линейных уравнений методом Крамера .

5. Решить систему линейных однородных уравнений .

Векторная алгебра

1. Даны три вектора .

Найти: вектор ; длины векторови; скалярное произведение векторови; векторное произведение векторови; длину вектора; смешанное произведение векторов,и. Проверить, будут ли коллинеарны или ортогональны векторы и;будут ли компланарны векторы ,и.

2. Даны точки .Найти: площадь треугольника , объем пирамиды

Аналитическая геометрия

1. Даны точки . Составить: уравнения сторон и , уравнение высоты, уравнение медианы.

2. Записать уравнение эллипса и построить кривую, если его малая полуось 2, а координаты фокусов .

3. Записать уравнение гиперболы и построить кривую, если его действительная полуось , а координаты фокусов.

4. Даны четыре точки . Составить уравнение плоскости , найти ее нормальный вектор; составить уравнение прямой, найти направляющий вектор прямой; записать уравнение прямой, перпендикулярной к плоскости; записать уравнение прямой, параллельной прямой; записать уравнение плоскости, проходящей через точку, перпендикулярно к прямой.

Предел и непрерывность функции

1. Вычислить предел .

2. Вычислить предел .

3. Вычислить предел .

4. Исследовать функцию на непрерывность и построить график .

5. Исследовать функцию на непрерывность и построить график .

Контрольная работа по математике №1 (УТС)

Вариант 1.

Комплексные числа

1. . Найти.

2. . Найти.

3. . Найти модуль и аргумент комплексного числа.

4. . Записать в тригонометрической форме число.

5. . Найти.

6. . Найти.

Линейная алгебра

1. Даны матрицы и. Найти:

; ;;.

2. При каком значении определительравен нулю.

3. При каком значении матрицавырождена.

4. Решить систему линейных уравнений методом Крамера .

5. Решить систему линейных однородных уравнений .

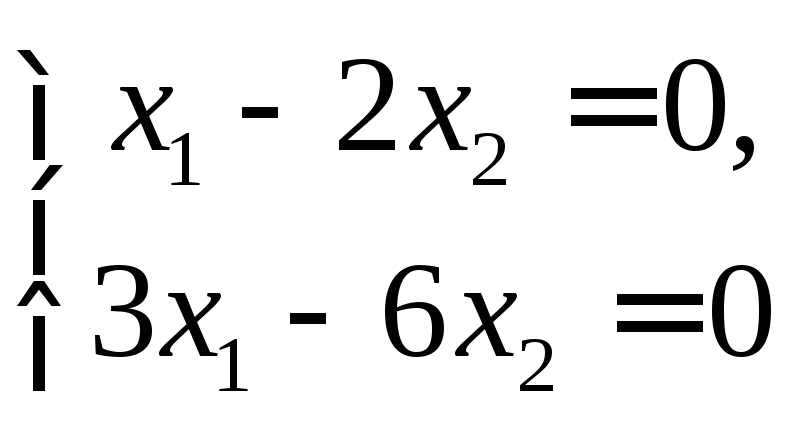Векторная алгебра

1. Даны три вектора .

Найти: вектор ; длины векторови; скалярное произведение векторови; векторное произведение векторови; длину вектора; смешанное произведение векторов,и. Проверить, будут ли коллинеарны или ортогональны векторы и;будут ли компланарны векторы ,и.

2. Даны точки .Найти: площадь треугольника , объем пирамиды

Аналитическая геометрия

1. Даны точки . Составить: уравнения сторон и , уравнение высоты, уравнение медианы.

2. Записать уравнение эллипса и построить кривую, если его полуось , а координаты фокусов.

3. Записать уравнение гиперболы и построить кривую, если его действительная полуось , а координаты фокусов.

4. Даны четыре точки . Составить уравнение плоскости , найти ее нормальный вектор; составить уравнение прямой, найти направляющий вектор прямой; записать уравнение прямой, перпендикулярной к плоскости; записать уравнение прямой, параллельной прямой; записать уравнение плоскости, проходящей через точку, перпендикулярно к прямой.