1.4.Методические особенности изучения площади геометрических фигур и единиц ее измерения на уроках математики в начальной школе.

Методика формирования представлений о площади фигуры строится в соответствии с общей методикой формирования представлений о величинах. При этом изучение понятия площади проводится с опорой на привычные для детей представления о том, что каждая фигура занимает определенное - большее или меньшее – место на плоскости (Приложение 10).

Для того чтобы учащиеся освоили процесс измерения площади полезно раздать им геометрические фигуры и предложить им измерить их площади, пользуясь моделью квадратного сантиметра. Это задание особенно важно, так как в процессе его выполнения учащиеся осознают, что измерить площадь фигуры – значит узнать, сколько квадратных сантиметров она содержит. Учащиеся практически убеждаются, что укладывать модель квадратного сантиметра в фигуре долго и неудобно – гораздо удобнее использовать прозрачную бумагу, на которой нанесена сетка из квадратных сантиметров. Таким образом, учащиеся знакомятся с палеткой и правилами пользования ею, упражняются в определении площадей фигур с ее помощью.

При определении площади прямоугольника необходимо также широко использовать практический метод. Это поможет учащимся осознать тот факт, что найти площадь прямоугольника – значит узнать, сколько квадратных сантиметров в нем содержится .

В методике работы над площадью фигуры имеется много общего с работой над длиной отрезка.

Прежде всего, площадь выделяется как свойство плоских предметов среди других их свойств. Уже дошкольники сравнивают предметы по площади и правильно устанавливают отношения "больше", "меньше", "равно", если сравниваемые предметы резко отличаются друг от друга или совершенно одинаковые. При этом дети пользуются наложением предметов или сравнивают их на глаз, сопоставляя предметы по занимаемому месту на столе, на земле, на листе бумаги и т.п. однако, сравнивая предметы, у которых форма различна, а различие площадей не очень четко выражено, дети испытывают затруднения. В этом случае они заменяют сравнение по площади сравнением по длине или по ширине предметов, т.е. переходят на линейную протяженность, особенно в тех случаях, когда по одному из измерений предметы сильно отличаются друг от друга.

В процессе изучения геометрического материала в I – II классах у детей уточняются представления о площади как о свойстве плоских геометрических фигур. Более четким становится понимание того, что фигуры могут быть различными и одинаковыми по площади. Этому способствуют упражнения на вырезание фигур из бумаги, черчение и раскрашивание их в тетрадях и т.п. В процессе решения задач с геометрическим содержанием учащиеся знакомятся с некоторыми свойствами площади. Они убеждаются, что площадь не изменяется при изменении положения фигуры на плоскости (фигура не становится ни больше, ни меньше). Дети многократно наблюдают соотношение между всей фигурой и ее частями (часть меньше целого), упражняются в составлении различных по форме фигур из одних и тех же заданных частей (т.е. построение равносоставленных фигур). Учащиеся постепенно накапливают представления о делении фигур на неравные равные части, сравнивая наложением полученные части, сравнивая наложением полученные части. Все эти знания и умения дети приобретают практическим путем попутно с изучением самих фигур(Приложение 11).

Однако не всегда так легко установить, какая из двух фигур имеет большую (меньшую) площадь или они одинаковы по площади. Чтобы показать это учащимся, можно предложить им сравнить вырезанные из бумаги прямоугольник и квадрат, незначительно отличающиеся по площади, например: размеры квадрата 4х4 дм, а прямоугольника 5х3 дм, при этом фигуры с обратной стороны разбиты на квадратные дециметры. Сначала учащиеся пытаются сравнить эти фигуры на глаз, а также путем наложения. Однако оба способа не помогают детям решить вопрос убедительно. Выслушав различные предположения, учитель поворачивает фигуры той стороной, на которой сделана разбивка на квадраты, и предлагает сосчитать, сколько одинаковых квадратов содержит каждая фигура. На этой основе дети устанавливают, площадь какой фигуры больше, а какой меньше. Аналогичные упражнения на сравнивание площади фигур, составленных из одинаковых квадратов, выполняются по учебнику, а также по чертежам, данным на доске. Дети убеждаются в том, что если фигуры состоят из одинаковых квадратов, то площадь той фигуры больше (меньше), которая содержит больше (меньше) квадратов. Полезно на этом же уроке рассмотреть такой случай, когда разные по форме фигуры имеют одинаковую площадь, так как содержат одинаковое число квадратов. На последующих уроках включаются упражнения на подсчет квадратов, содержащихся в заданных фигурах, предлагается начертить в тетрадях фигуры, которые состоят из заданного числа квадратов (клеточек тетради). В процессе таких упражнений начинает формироваться понятие о площади как о числе квадратных единиц, содержащихся в геометрической фигуре .

На следующем этапе учащихся знакомят с первой единицей площади – квадратным сантиметром. Учащиеся чертят в тетрадях, вырезают из бумаги в клеточку квадраты со стороной 1см. учитель сообщает: "это единица площади – квадратный сантиметр". Используя бумажные модели квадратного сантиметра, дети составляют из них различные геометрические фигуры и находят подсчетом их площадь. Сравнивая площади составленных фигур, дети еще раз убеждаются, что площадь той фигуры больше (меньше), которая содержит больше (меньше) квадратных сантиметров. Площади фигур содержащих одинаковое число квадратных сантиметров, равны, хотя фигуры могут не совмещаться наложением. Эффективен на этом этапе прием сопоставления знакомых детям величин – длины отрезка и площади фигуры, который помогает предупредить смещение этих величин. Выполняя конкретные упражнения, обнаруживают некоторое сходство и существенное различие этих величин: сантиметр – единица длины; квадратный сантиметр – единица площади; длина отрезка – число сантиметров, которые содержаться в данном отрезке; площадь фигуры – число квадратных сантиметров, содержащихся в этой фигуре.

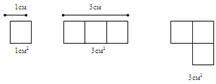
В дальнейшем наглядное представление о квадратном сантиметре и понятие о площади фигур закрепляются. Включаются упражнение на площади фигур, разбитых на квадратные сантиметры. Предлагается при подсчете квадратных сантиметров группировать их по рядам или столбцам, чтобы ускорить нахождение их общего числа. Рассматриваются и такие фигуры, которые на ряду с целыми квадратными сантиметрами содержат и нецелые – половины, а также доли больше или меньше, чем половина квадратного сантиметра. Следует также ознакомить учащихся с нахождением приближенной площади фигуры таким способом: сосчитать все нецелые квадратные сантиметры и общее число их разделить на два, затем полученное число сложить с числом целых квадратных сантиметров, которые содержатся в данной фигуре . Для нахождения площади геометрических фигур, не разделенных на квадратные сантиметры, используют палетку.Палетка – это прозрачная пластинка, разбитая на равные квадраты. Сетка может быть нанесена на кальку или состоять из нитей, натянутых на рамку. На данном этапе используют палетку, каждое деление которой равно квадратному сантиметру.

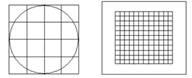
Наложив палетку на геометрическую фигуру, подсчитывают число целых и нецелых квадратных сантиметров, которые в ней содержатся. Для нахождения площади фигур, начерченных в тетрадях, в качестве палетки используют разлиновку тетрадей. Каждый раз подчеркивают, что найденная площадь равна приблизительно такому – то числу (около 20 см²).

В это же время приступают к сопоставлению площади и периметра многоугольников с тем, чтобы дети не смешивали эти понятия, а дальнейшем четко различали способы нахождения площади и периметра прямоугольника. Выполняя практические упражнения с геометрическими фигурами, дети подсчитывают число квадратных сантиметров и тут же измеряют периметр многоугольника в сантиметрах.

На следующем этапе учащиеся знакомятся с приемом вычисления площади прямоугольника (квадрата). Сначала рассматривают прямоугольники, которые уже разделены на квадратные сантиметры. Их площадь находят путем подсчета квадратных сантиметров в одном ряду, а затем полученном число умножают на число рядов. Очень важно при этом установить соответствие между длиной прямоугольника и числом квадратных сантиметров, прилегающих к длине; шириной прямоугольника и числом рядов.

Затем дети чертят прямоугольник по заданным длинам сторон, разбивают его на ряды, а один ряд на квадраты и снова убеждаются в соответствии: если длина 4 см, то в одном ряду, прилегающем к этой стороне, содержится 4 кв.см, если ширина 3 см, то таких радов оказывается 3. число квадратных сантиметров равно произведению чисел 4 и 3. делается вывод: чтобы вычислить площадь прямоугольника, нужно знать его длину и ширину (в одинаковых единицах) и найти произведение этих чисел.

В процессе решения задач на вычисление площади и периметра прямоугольников следует показать, что фигуры, имеющие одинаковую площадь, могут иметь неодинаковые периметры, и что фигуры, имеющие одинаковые периметры, могут иметь неодинаковые площади. Например, это легко наблюдать при заполнении таблицы вида:

Таблица 1.

Длина	7 см	6 см	5 см	4 см
Ширина	1 см	2 см	3 см	4 см
Периметр	16 см	16 см	16 см	16 см
Площадь	7 см2	12 см2	15 см2	16 см2

Далее учащиеся знакомятся с дм². Как и при введении см², прежде всего формируется наглядный образ новой единицы: дети чертят на клетчатой бумаге квадрат со стороной 1 дм и затем вырезают его, составляют фигуры из нескольких квадратных дециметров, называя их площадь и периметр. Устанавливается соотношение между квадратным дециметром и квадратным сантиметром: 1 дм² = 100 см². для этого просто вычисляется площадь квадрата со стороной 1 дм = 10 см (10*10 = 100). Учащиеся сами вычисляют площадь квадрата со стороной 1 дм в квадратных сантиметрах и записывают: 1 дм² = 100 см² затем дети учатся заменять мелкие единицы крупными и наоборот. Для достижения возможности решать задачи с данными, полученными путем непосредственных измерений при выполнении практических работ, необходимо выполнить ряд упражнений: "Выразить в см²: 2 дм²; 1 дм² 74 см² и т.п. Выразить в дм² и см²: 570 см²; 1250 см²" .

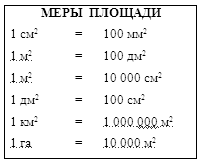
На следующем этапе аналогично рассматривается квадратный метр. Обращается особое внимание на решение практических задач. Должна быть составлена и усвоена таблица всех изученных единиц площади и их отношений.

Наряду с решением задач на нахождение площади прямоугольника по данным длине и ширине решают обратные задачи на нахождение одной из сторон по известной площади и другой стороне прямоугольника.

Вывод: Задача развития у младших школьников геометрических представлений, способности к обобщению состоит в том, чтобы научить их видеть геометрические образы в окружающей обстановке, выделять их свойства, конструировать, преобразовывать и комбинировать фигуры, изображать их на чертеже, выполнять в необходимых случаях измерения.

Учебные задания практического характера являются средством и условием формирования способности использовать универсальные знания и умения, развития интереса к исследованию проблем окружающего мира.

Включение заданий практического характера в учебную деятельность позволяет использовать приобретённые знания и умения в практической деятельности и повседневной жизни для ориентировки в окружающем пространстве; сравнения и упорядочения объектов по разным признакам;

Решения задач, связанных с бытовыми жизненными ситуациями; оценки размеров предметов «на глаз»; самостоятельной конструкторской деятельности.

90. Пути организации творческой деятельности на уроках литературного чтения: метод «творческого чтения» (по Н.И. Кудряшёву); характеристика творческих приемов деятельности на уроках литературного чтения (драматизация, творческий пересказ, словесное и графическое рисования и т.д.).

Можно считать общепризнанным положение о том, что творчество учащихся (и руководство педагогов этой деятельностью) имеет своей конечной целью не столько создание определенного продукта, имеющего общественно полезную значимость, сколько познавательный и воспитательный эффект - формирование знаний, умений интересов и склонностей, развитие способностей личности.

Педагогический аспект творчества характеризуется рядом субъективных факторов: спецификой самого процесса творчества, эмоциональностью, развитием личности индивида, ростом его мастерства. Эти факторы в полной мере присущи и творческой деятельности учащихся. Поэтому именно педагогический аспект придает важность творчеству в школьном возрасте. Различные виды любительских увлечений играют огромную роль в образовании, воспитании и развитии подрастающего поколения, поэтому необходимо включение школьников в творческую деятельность как в процессе изучения основ наук, так и во внеклассной работе.

Опыт учителей, организующих творческую деятельность учащихся, а также проводимые в этом направлении специальные исследования, позволяет указать основные условия, необходимые для развития творческих способностей учащихся и рекомендовать оправдавшие себя на практике пути решения этой проблемы. К ним относятся

- приложения в учебном процессе методов, содействующих развитию у учащихся логического мышления, инициативы, активности и самостоятельности;

- включение элементов исследования в различные виды учебной деятельности учащихся;

- организация индивидуальных учебных занятий творческого характера.

Беда нашей школы и нашего общества в том, что целые поколения прошли мимо искусства, в том, что литература в нашей школе с самых первых классов преподавалась не как искусство, а лишь с целью познания различных явлений, событий, праздников и т.п. Методика была направлена на главным образом на усвоение этих знаний.

В методике долгое время ведется борьба с логилизированным чтением художественной литературы. При логилизированном чтении главное внимание учителя и учащихся сосредотачивается на уяснении сюжета 0 событийных связей с помощью многочисленных вопросов: что, где, куда, почему? С помощью этих вопросов выявляются логические связи произведений, и это является основной работой над его пониманием. Далее идет словарная работа: уясняются все непонятные, с точки зрения логики познания, слова, в том числе и художественные средства - опять же путем их логического толкования, то есть художественные средства - опять же путем их логического толкования, то есть художественное слово перевести на бытовой, нехудожественный язык, именуя и заглушая тем самым его художественный смысл. Устное рисование, которое тоже превращается часто в перевод художественного образа в его пересказ простыми словами, мало что добавляет к пониманию художественного произведения.

Учебные программы предполагают такое содержание учебных книг, их структуру и технологию обучения, которые строятся на основе двух ведущих принципов: художественно-эстетического и литературоведческого.

Художественно-эстетический принцип определяет стратегию отбора произведений для чтения и вводит а круг чтения младших школьников преимущественно художественные тексты. Он акцентирует внимание учителя и детей на том, что перед ними не просто познавательные интересные тексты, а именно произведения словесного искусства, которые раскрывают перед читателем богатство окружающего мира и человеческих отношений, рождают чувство гармонии, красоты, учат понимать прекрасное в жизни, формируют в ребенке собственное отношение к действительности.

Литературоведческий принцип в его специфическом преломлении к особенностям начального этапа обучения реализуется при анализу художественного текста. Он требует, чтобы на первый план был выдвинут художественный образ как общий язык искусства в целом и литературы в частности.

Отличной особенностью программы литературного чтения является введение ее содержания раздела: «Опыт творческой деятельности и опыт направленного эмоционально-чувственного отношения к действительности». Введение такого раздела в программу привело к включению в процесс обучения тех приемов и способов деятельности детей, которые помогают им воспринимать художественное произведение на основе проявления собственных творческих способностей, ибо чтение прежде всего сотворчество. Литература относится к наиболее сложному, интеллектуальному виду искусства, восприятие произведений которого носит опосредованный характер, при чтения человек получает тем большее наслаждение художественными образами, чем ярче оказываются представления, которые возникают у него в процессе чтения. Характер и полнота восприятия литературного произведения во многом определяются конкретно-чувственным опытом и умением ребенка воссоздать словесные образы, соответствующие авторскому тексту.

Таким образом, курс литературного чтения преследует решение следующих задач:

- развивать у детей способность полноценно воспринимать художественное произведение, сопереживать героям, эмоционально откликаться на прочитанное;

- учить детей чувствовать и понимать образный язык художественного произведения, развивать образное решение;

- формировать умение воссоздать художественные образы литературного произведения, развивать творческое и воссоздающее воображение учащихся;

- обеспечивать развитие речи учащихся и активно формировать речевые умения, навыки чтения, слушания и др.

Как мы видим, все вышеперечисленные задачи решаются только на основе активной творческой деятельности учащихся при помощи воображения.

Известно, что искусство возникло в истории цивилизации для того, чтобы развивать и поддерживать фундаментальную основополагающую человеческую способность - воображение. Человек, лишенный воображения, не может понять другого человека. Чтобы действовать в разных ситуациях, возникающих на каждом шагу, нужно воображение - нужно вообразить, представить себя в иной ситуации.

Чтобы продвигать детей в развитии, надо отказаться от известных стереотипов работы на уроках чтения и направить ее так, чтобы ученики воспринимали и ценили художественное слова как незаменимое, над глубоким содержанием которого надо думать. Так, чтобы чтение каждого нового произведения или перечитывания известного ранее, было бы для них новым открытием, вызывало работу души - чувств, воображения, затрагивало их жизненный опыт, то есть захватывало бы их личность.

По определению Н.И. Кудряшева, метод творческого чтения тесно связан с основной задачей, решаемой учителем на уроке литературы: «развивать и совершенствовать глубокое, возможно ,более активное и полное, творческое восприятие художественного произведения, художественные переживания школьников».

Специфика метода творческого чтения заключается в активизации художественного восприятия, художественных переживаний, в формировании средствами искусства художественных склонностей и способностей.

Метод творческого чтения проявляется большей частью через следующие приемы: 1) выразительное (в идеале – художественное) чтение учителя, чтение мастеров художественного слова, отдельных сцен из пьес в исполнении актеров (в записях, в радио- и телепередачах); 2) обучение выразительному чтению учащихся; 3) чтение учителем художественного текста с комментариями (комментированное чтение) и 4) его слово, имеющее целью обеспечить правильное и возможно более глубокое, эмоциональное восприятие произведения; 5) беседа, имеющая целью выяснить непосредственные впечатления учащихся от прочитанного произведения и направляющая их внимание на существенные его идейные и художественные особенности, или постановка той или иной – художественной, нравственной, общественно-политической – проблемы, непосредственно вытекающей из прочитанного произведения; 6) слово учителя или беседа после изучения произведения, имеющие целью активизировать художественные переживания учащихся, обогащенные в процессе его изучения.

Метод творческого чтения способствует развитию наблюдательности, умению видеть и слышать явления жизни, умению найти верные слова и выражения для передачи своих впечатлений путем выполнения различного рода творческих заданий: обучение творческим работам по живым, непосредственным наблюдениям, по картинам, по кинокартинам, спектаклям…, только что прочитанным книгам… - все это проявление метода творческого чтения.

Все эти приемы предполагают соответствующие виды деятельности учащихся: чтение произведений дома и в классе, выразительное (в идеале - художественное) чтение, заучивание наизусть, слушание художественного чтения, составление плана, заголовки которого стимулируют образное, эмоциональное воспроизведение отдельных эпизодов, сцен произведения, близкие к тексту и сжатые пересказы, художественное рассказывание, устные и письменные отзывы о только что прочитанном произведении, инсценировки, составление сценариев, критические заметки, рассматривание иллюстраций и оценка их, сочинения разного жанра по картинам, по живым впечатлениям.

Т.о. каждый примененный учителем прием должен быть связан в соответствующим видом деятельности учащихся.

Необходимо дать некоторые пояснения к термину «художественное рассказывание».

Художественное рассказывание – это один из видов искусства устного слова, заключающийся в передаче слушающим идейно-художественного содержания повествовательного прозаического произведения в живой собственной речи рассказчика с целью вызвать у них те представления, мысли и чувства, которые возникают у самого исполнителя в процессе его творчества. В основе художественного рассказывания лежат те же принципы, что и в основе выразительного чтения. Однако, если чтец точно передает текст автора, то рассказчик – всегда импровизирует.

Иногда рассказывание называют художественным пересказом. По своей структуре оно действительно является воспроизведением текста в той последовательности ,в которой он воспринимается при чтении, но существенно отличается от пересказа, опирающегося на репродуктивную деятельность. Рассказывание возможно только в том случае, если исполнитель овладеет и передаст в речи не только текст, но и подтекст литературного произведения. Главное в художественном рассказывании – его коммуникативная функция, выражающаяся в умении рассказчика проявить свое личное отношение к исполняемому тексту, воздействовать словом на ум , чувства и эмоции слушателей, полностью убедить их своим рассказом. Рассказывание не может быть нехудожественным. Художественность, т.е. образность, живость, воздейственность, - отличительная черта этого вида деятельности.

Билет 91. Пед. процесс в начальной школе.

Лекция 10. Педагогический процесс